Blog Professor Emerson

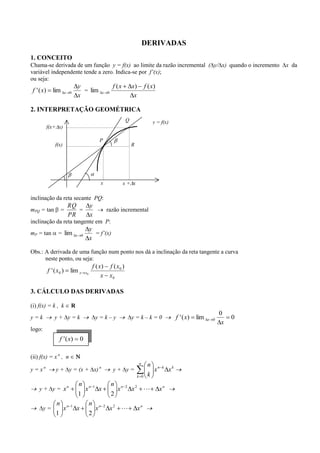
1. DERIVADAS
1. CONCEITO
Chama-se derivada de um função y = f(x) ao limite da razão incremental ( y/ x) quando o incremento x da
variável independente tende a zero. Indica-se por f’(x);
ou seja:
y f (x x) f ( x)
f ' ( x) lim x 0 = lim x 0
x x
2. INTERPRETAÇÃO GEOMÉTRICA
Q y = f(x)
f(x+ x)
P
f(x) R
x x+ x
inclinação da reta secante PQ:
RQ y
mPQ = tan = = razão incremental
PR x
inclinação da reta tangente em P:
y
mP = tan = lim x 0 = f’(x)
x
Obs.: A derivada de uma função num ponto nos dá a inclinação da reta tangente a curva
neste ponto, ou seja:
f ( x) f ( x0 )
f ' ( x0 ) lim x x0
x x0
3. CÁLCULO DAS DERIVADAS
(i) f(x) = k , k R
0
y=k y+ y=k y=k–y y=k–k=0 f ' ( x) lim x 0 0
x
logo:
f ' ( x) 0
(ii) f(x) = x n , n
n n
y = xn y + y = (x + x) n y+ y= xn k
xk
k 0 k
n n
y + y = xn xn 1
x xn 2
x2  xn
1 2
n n
y= xn 1
x xn 2
x2  xn
1 2

2. n n n n2
x( x 1
x x  xn 1 )
1 2 n n 1
f ’(x) = lim x 0 x n.x n 1
x 1
logo:
f ' ( x) n.xn 1
(iii) f(x) = x –1
1 1 1 1
y = x –1 y+ y= y= –y y= –
x x x x x x x
1 1 x x x
x x x x( x x) x 1
f ' ( x) lim x 0 lim x 0 lim x 0
x x x( x x) x
1 1 2
= lim x 0 x
x( x x) x2
logo:
f ' ( x) x 2
(iv) f(x) = sen x
y = sen x y + y = sen(x + x) y = sen(x + x) – y y = sen(x+ x) – sen x
x x x x x x x x
y = 2 sen . cos y = 2.sen .cos(x + )
2 2 2 2
2. sen x / 2 cos(x x / 2)
f ' ( x) lim x 0 =
x
sen x / 2
= lim x 0 . lim x 0 cos(x x / 2) cos x
x/2
logo:
f ' ( x) cos x
(v) f(x) = cos x
y = cos x y + y = cos(x + x) y = cos(x + x) – y y = cos(x+ x) – cos x y=-
x x x x x x x x
2 sen . sen y = -2.sen .sen(x + )
2 2 2 2
2. sen x / 2 sen(x x / 2)
f ' ( x) lim x 0 =
x
sen x / 2
= lim x 0 . lim x 0 sen(x x / 2) sen x
x/2
logo:
f ' ( x) sen x
2

3. (vi) f(x) = a x , a R+ – {1}
y = ax y + y = a (x + x) y + y = a x.a x
y = a x.a x
–y
y = a .a – a
x x x
y = a (a x – 1)
x
a x (a x
1) x a x
1
f ' ( x) lim x 0 lim x 0 a . lim x 0 a x . ln a
x x
logo:
f ' ( x) a x .ln a
4. PROPRIEDADES
(i) f = u + v f’ = u’ + v’
( u( x x) v( x x) ) ( u ( x) v( x) )
com efeito, f(x) = u(x) + v(x) f ’(x) = lim x 0 =
x
u( x
x) u ( x) v( x x) v( x)
= lim x 0 lim x 0 u ' ( x) v ' ( x)
x x
generalizando: f f1 f 2  f n f ' f1 ' f 2 '  f n '
Obs.: f = u – v f ’ = u’ – v’
(ii) f = u v f ’ = u’ v + u v’
( u( x x) v( x x) ) ( u ( x) v( x) )
com efeito, f(x) = u(x). v(x) f’(x) = lim x 0 =
x
u( x x) v( x x) u ( x x) v( x) u ( x x).v( x) u ( x) v( x)
= lim x 0
x
u( x x ) (v ( x x) v( x)) v( x) (u ( x x) u ( x))
= lim x 0
x
v( x x) v( x) u( x x) u ( x)
= lim x 0 u( x x) lim x 0 v( x)
x x
= u ' ( x).v( x)
u( x).v ' ( x)
generalizando: f f1 . f 2 .. f n f' f1 '. f 2 .. f n f1 . f 2 '. f n  f1 . f 2 .. f n '
Obs: f(x) = k.u(x) f’(x) = 0.v(x) + k.v’(x) f’(x) = k.v’(x), k R
u uv ' vu '
(iii) f f'
v v2
u( x
x) u ( x)
v( x
x) v( x) u( x x).v( x) u ( x).v( x x)
com efeito, f ' ( x) lim x 0 lim x 0
x x.v( x).v( x x)
u( x x).v( x) u ( x).v( x) u ( x).v( x) u ( x).v( x x) 1
= lim x 0 .
x v( x).v( x x)
u( x x) u ( x) v( x x) v( x) 1
(lim x 0 v( x) lim x 0 u ( x) ) lim x 0
x x v( x).v( x x)
u ' ( x).v( x) u ( x).v ' ( x)
=
v 2 ( x)

4. 5. REGRA DA CADEIA
Se y = f(u), u = g(x) e as derivadas f’(u) e g’(x) existem, então a função composta definida por y = fog(x)
tem derivada dada por y’ = f ’(u) . g’(x)
demonstração:
com efeito,
y = f(g(x + x)) – f(g(x))
u = g(x + x) – g(x) g(x + x) = g(x) + u = u + u
y
f ’(u) = lim u 0
u y y u y u
u f ' ( x) lim x 0 lim x 0 . lim x 0 . lim x 0
g’(x) = lim x 0
x u x u x
x
se x 0 então g(x + x) g(x) e u 0
y u
logo: f ' ( x) lim u 0 . lim x 0 f ' (u ).g ' ( x)
u x
Ex.: y = (x 2 + 1) 3
y = u3 y’ = 3u2
u = x2 + 1 u’ = 2x fy’ = 3.(x2 + 1)2.2x = 6x.(x2 + 1)2
generalizando: f f1of 2 o  of n f' f n '. f n 1 '.. f1 '
1
Obs.: Seja f uma função cuja derivada é f ’ e inversa é f –1. f –1’(x) =
f ' o f 1 ( x)
log x
Ex.: f(x) = a x f –1(x) = log a x f ’(x) = a x ln a f ’of –1(x) = a a ln a
1
f –1’(x) =
x ln a
1
logo: y = log a x y’ =
x ln a
6. DIFERENCIAL DE UMA FUNÇÃO
6.1. CONCEITO
Dada uma função y = f(x), derivável, chama-se diferencial desta função ao produto de sua derivada pelo
acréscimo da variável independente, indica-se por: dy = f’(x).dx
6.2.INTERPRETAÇÃO GEOMÉTRICA
S
PRS, temos:
Q
y = f(x) RS = PR . tan
P R PR = dx e tan = f”(x)
ff’(x).dx = RS
logo: dy = RS
x x+ x
A diferencial de uma função é o acréscimo da ordenada da tangente a curva num ponto P, quando é dado um
acréscimo a variável independente.
4

5. Obs.: Para valores pequenos de x temos y dy, isto é, o acréscimo da função é aproximadamente igual a
sua diferencial
Ex.: Calcular o acréscimo e a diferencial da função f(x) = x2, para x = 2 e x = 0,1.
y = x2 y + y = (x + x)2 y + y = x2 + 2.x. x + ( x)2
2
y = 2.x. x + ( x) acréscimo
dy = 2x.dx diferencial
x = 2 e x = dx = 0,1 ; temos:
y = 2.2.0,1 + 0,12 = 0,4 + 0,01 = 0,41
dy = 2.2.0,1 = 0,4
7. TEOREMA
Se uma função é derivável num ponto, então ela é contínua neste ponto.
demonstração:
com efeito,
f ( x) f ( a )
f(x) – f(a) = ( x a) , x a
x a
f ( x) f ( a )
lim x a ( f ( x) f (a)) lim x a ( x a)
x a
f ( x) f (a )
lim x a f ( x) lim x a f (a) lim x a lim x a ( x a)
x a
(lim x a f ( x)) f (a) f ' (a) 0 (lim x a f ( x)) f (a) 0
lim x a f ( x) f (a)
logo: f(x) é contínua para x = a
Obs.: A recíproca desse teorema não é verdadeira, isto é, uma função pode ser contínua num ponto e no entanto
não ser derivável no ponto.
8. DERIVADAS SUCESSIVAS
8.1 CONCEITO
A derivada primeira de uma função y = f(x), normalmente ainda é uma função derivável. Derivando a derivada
primeira obtemos a derivada segunda da função; derivando a derivada segunda obtemos a derivada terceira da
função e assim sucessivamente. Indica-se por: f’(x), f’’(x), f’’’(x), f (4)(x), ... , f (n)(x)
Ex.: f(x) = e2x
y’ = 2e2x
y’’ = 4e2x
y’’’ = 8e2x
__ __ __ __
(n) n 2x
y =2 e
8.2. REGRA DE LEIBNITZ
n n (n
f u v f ( n) u k)
v (k )
k 0 k
com efeito,
f = u.v f ’ = u’.v + u.v’ f ’’ = u’’.v + u’.v’ + u’.v’ + u.v’’ = u’’.v + 2u’.v’ + u.v’’ f ’’’ = u’’’.v +
u’’.v’ + 2.(u’’.v’ + u’.v’’) + u’v’’ + u.v’’’ =
= u’’’.v + 3.u’’.v’ + 3.u’.v’’ + u.v’’’ ...
n n n
f ( n) u ( n) v u ( n 1) v' u (n 2)
v' '  u' v ( n 1) u v ( n)
1 2 n 1

6. Ex.: f(x) = e ax.x 2
u(x) = e ax u’(x) = a.e ax u’’(x) =a2.e ax u’’’(x) = a3.eax ...
(n) n ax
u (x) = a .e
v(x) = x 2 v’(x) = 2x v’’(x) = 2 v’’’(x) = 0
v (4)(x) = v (5)(x) = ... = v (n)(x) = 0
n n-1 ax n n-2 ax
f (n)(x) = a n.e ax. x 2 + .a .e .2x + a .e .2 =
1 2
= an - 2.e ax.( a2.x2 + 2.n.a.x + n.(n – 1))
9. DERIVAÇÃO DE FUNÇÕES IMPLÍCITAS
Funções implícitas são aquelas que se apresentam sob a forma F(x, y) = 0, onde y = f(x)
3x 2 x2
Exs.: (i) x 3 y3 9 0 3x 2 3 y 2 y' 0 y' y'
3y 2 y2
(ii) ( x y ) 2 ( x y ) 2 x 4 y 4 2( x y )(1 y ' ) 2( x y )(1 y ' ) 4x3 4 y 3 y'
2 x 2 y 2 xy ' 2 yy ' 2 x 2 y 2 xy ' 2 yy ' 4 x 3 4 y 3 y '
4( y x 3 ) x3 y
y ' (4 y 3 4 x) 4 y 4x 3 y' y'
4( y 3 x) x y3
10. TAXAS RELACIONADAS
Sejam x = f(t) e y = g(t) duas funções diferenciáveis e F(x, y) = 0 uma função
y = f(x) na forma implícita. As derivadas dx/dt e dy/dt nesta função implícita chamam-se taxas relacionadas
da função.
Ex.: Uma escada de 5m de comprimento está apoiada numa parede vertical. Se a base da escada é arrastada
horizontalmente da parede a 3m/s, a que velocidade desliza a parte superior da escada ao longo da parede,
quando a base encontra-se a 3m da parede ?
5m
y
x
x2 y2 25
dx
2x
dx dy dy dt x dx 3
2x 2y 0 3 2,25 m/s
dt dt dt 2y y dt 4
logo: a parte superior da escada desliza com a velocidade de 2,25 m/s
6

7. 11. REGRA DE L’HOSPITAL
f ( x) 0 f ' ( x)
Se lim x a está indeterminado do tipo ou e existe lim x a , então
g ( x) 0 g ' ( x)
f ( x) f ' ( x)
lim x a lim x a
g ( x) g ' ( x)
x2 9 2x
Ex.: lim x 3 lim x 3 6
x 3 1
12. TEOREMA DE ROLLE
Se f é uma função contínua no intervalo [a, b], derivável no intervalo (a, b) e
f(a) = f(b), então existe pelo menos um número real c entre a e b tal que f ’(c) = 0
demonstração:
com efeito,
se f é uma função constante no intervalo dado, então f ’(x) = 0 e o teorema é satisfeito para todo x pertencente
ao intervalo dado
senão f não é constante e apresenta pelo menos um máximo M ou um mínimo m no intervalo dado
suponhamos que f no intervalo dado, apresenta um mínimo m = f(c) , temos:
f(x) – f(c) 0, x V(c)
f ( x ) f (c ) f ( x ) f (c )
lim x c
0 e lim x c
0
x c x c
f ( x ) f (c )
se f ’(c) então lim x c
0
x c
logo: f ’(c) = 0
Ex.: f(x) = sen x no intervalo [0, 2 ]
f é contínua em [0, 2 ]
f é derivável em (0, 2 )
f(0) = f(2 ) = 0
f ’(x) = cos x , cos x = 0 x = /2 ou x = 3 /2
Obs.: (i) se a função não é contínua em todo intervalo [a, b] , o Teorema de Rolle não se
aplica, isto é, não podemos garantir a existência do ponto c tal que f ’(c) = 0
(ii) se a função não é derivável em todo intervalo (a, b) , o Teorema de Rolle não
se aplica, isto é, não podemos garantir a existência do ponto c tal que f ’(c) = 0
(iii) o Teorema de Rolle nos diz que existe pelo menos um ponto c entre a e b no
qual a reta tangente paralela ao eixo dos x
13. TEOREMA DE LAGRANGE (TEOREMA DO VALOR MÉDIO)
Se f é uma função contínua no intervalo [a, b] e derivável no intervalo (a, b) , então existe pelo menos um
f (b) f (a)
número real c entre a e b tal que f ' (c)
b a
demonstração:
com efeito,
consideremos a equação da reta que passa pelos pontos (a, f(a)) e (b, f(b)):
f (b) f (a)
y ( x a) f (a)
b a
consideremos uma função auxiliar F(x) que nos dá a distância vertical entre um ponto da função e o ponto
correspondente da reta secante:
f (b) f (a)
F ( x) f ( x) ( ( x a) f (a))
b a
vamos verificar se F(x) satisfaz ao Teorema de Rolle:
(i) F(x) é contínua em [a, b] , pois é a soma de duas funções contínuas

8. f (b) f (a)
(ii) F(x) é derivável em (a, b), pois F ' ( x) f ' ( x)
b a
(iii) F(a) = F(b) = 0
vemos assim que o Teorema de Rolle pode ser aplicado à função F(x) no intervalo [a, b], isto significa que
existe pelo menos um número real c entre a e b tal que F’(c) = 0;
f (b) f (a)
F’(c) = 0 f ' (c ) 0
b a
f (b) f (a)
logo: f ' (c)
b a
Ex.: f(x) = x3 no intervalo [-2, 2]
f é contínua em [-2, 2]
f é derivável em (-2, 2)
f (b) f (a) f ( 2) f ( 2) 2 3
f ' (c ) 3 c2 3 c2 4 c
b a 2 ( 2) 3
Obs.: o Teorema de Lagrange nos diz que existe pelo menos um ponto c entre a e b no
qual a reta tangente a curva é paralela a reta secante que passa pelos pontos
(a, f(a)) e (b, f(b))
14. TEOREMA DE CAUCHY
Se f e g são funções contínuas no intervalo [a, b] , deriváveis no intervalo (a, b) e
g’(x) não se anula no intervalo (a, b) , então existe pelo menos um número real c entre a e b tal que
f ' (c ) f (b) f (a)
g ' (c ) g (b) g (a)
15. FUNÇÕES CRESCENTES E DECRESCENTES
Se f(x) é uma função contínua no intervalo [a, b] e derivável no intervalo (a, b) tem-se:
(i) f ’(x) 0, x (a, b) f é crescente em [a, b]
(ii) f ’(x) 0, x (a, b) f é decrescente em [a, b]
com efeito,
consideremos os valores x1 e x2 pertencentes ao intervalo (a, b) com x1 x2.
f ( x 2 ) f ( x1 )
pelo Teorema de Lagrange c | f ' (c )
x 2 x1
f(x2) – f(x1) = f ’(c) . (x2 – x1)
se f ’(c) 0 f(x2) – f(x1) 0 f(x2) f(x1) f(x1) f(x2) f é crescente
senão f ’(c) 0 f(x2) – f(x1) 0 f(x1) f(x2) f é decrescente
Ex.: f(x) = x2 f ’(x) =2x 2x = 0 x=0
x 0 f ’(x) 0 f é decrescente
x 0 f ’(x) 0 f é crescente
16. MÁXIMOS E MÍNIMOS
16.1. CONCEITO
Seja uma função f derivável no intervalo (a, b) e seja x0 um ponto desse intervalo. Dizemos que f apresenta
um máximo relativo ou local no ponto x0 , se x V(x0),
f(x) f(x0) ; analogamente, dizemos que f(x) apresenta um mínimo relativo ou local num ponto x0 se x
V(x0), f(x) f(x0)
Obs.: Para determinarmos os extremos de uma função devemos pesquisar os valores de x em que a derivada
primeira se anula e os pontos onde a derivada primeira não existe. Estes pontos críticos da função são os
possíveis extremantes da função
8

9. 16.2. TESTE DA SEGUNDA DERIVADA
Seja x0 um ponto crítico de uma função f(x) no qual f ’(x) = 0 e f ’(x) existe numa vizinhança de x0. Se f
’’(x) existe, então:
(i) f ’’(x0) 0 x0 é maximante
(ii) f ’’(x0) 0 x0 é minimante
com efeito,
se f ’’(x) 0 f ’(x) é decrescente
x x0 f ’(x) f ’(x0) f ’(x) 0 f(x) é crescente
x x0 f ’(x) f ’(x0) f ’(x) 0 f(x) é decrescente
logo: x0 é maximante
senão f’’(x) 0 f ’(x) é crescente
x x0 f ’(x) f ’(x0) f ’(x) 0 f(x) é decrescente
x x0 f ’(x) f ’(x0) f ’(x) 0 f(x) é crescente
logo: x0 é minimante
17. CONCAVIDADE
Seja y = f(x) a equação de uma curva , onde f(x) é uma função contínua, com derivadas contínuas:
(i) f ’’(x) 0 a curva tem a concavidade voltada para cima
(ii) f ’’(x) 0 a curva tem a concavidade voltada para baixo
Obs.: O ponto onde a curva muda de concavidade é chamado de ponto de inflexão da curva, nesse ponto a
derivada segunda se anula
18. ASSÍNTOTAS
18.1. CONCEITO
Seja y = f(x) a equação de uma curva. Uma reta r é uma assíntota à essa curva quando uma das coordenadas
x ou y de um ponto P da curva tende ao infinito, este ponto se aproxima indefinidamente da reta, isto é,
quando a função que dá a distância de P a r tem limite nulo
18.2. ASSÍNTOTA VERTICAL
A reta x = a é assíntota vertical de uma curva de equação y = f(x) , quando pelo menos uma das situações
abaixo ocorrer:
(i) lim x a f ( x)
(ii) lim x a
f ( x)
(iii) lim x a
f ( x)
(iv) lim x a
f ( x)
1
Ex.: (i) y
x 4
1 1
lim x 4
e lim x 4
x = 4 é assíntota vertical
x 4 x 4
(ii) y ln x
lim x 0 ln x x = 0 é assíntota vertical
18.3. ASSÍNTOTA HORIZONTAL
A reta y = b é assíntota horizontal de uma curva de equação y = f(x) , quando pelo menos uma das situações
abaixo ocorrer:
(i) lim x f ( x) b
(ii) lim x f ( x) b

10. 2x
Ex.: (i) y
x2 4
2x 2x
lim x 2 e lim x 2 y = 2 e y = -2 são
2
x 4 x2 4
assíntotas horizontais
(ii) y ex
lim x ex 0 y = 0 é assíntota horizontal
18.4. ASSÍNTOTA OBLÍQUA
A reta y = ax + b (a 0) é assíntota oblíqua de uma curva de equação y = f(x) , quando pelo menos uma das
situações abaixo ocorrer:
f ( x)
(i) a lim x e b lim x ( f ( x) ax)
x
f ( x)
(ii) a lim x e b lim x ( f ( x) ax)
x
com efeito,
y = f(x)
r
P
N M
Q
lim x PM 0
PM
PMN: PM = PN cos PN
cos
PM
lim x PN lim x 0
cos
PN = PQ – NQ lim x PN lim x ( f ( x) (ax b)) 0
f ( x) b
lim x ( f ( x) (ax b)) 0 lim x x( a ) 0
x x
f ( x) b f ( x) b
lim x ( a ) 0 lim x lim x a lim x ) 0
x x x x
f ( x) f ( x)
lim x ( ) a 0 a lim x ( )
x x
lim x ( f ( x) (ax b)) 0 lim x ( f ( x) ax) lim x b 0
lim x ( f ( x) ax) b 0 b lim x ( f ( x) ax)
Obs.: (i) a dedução feita vale também para o caso em que x -
(ii) só devemos pesquisar assíntota oblíqua na direção em que ocorreu assíntota
horizontal
10

11. (iii) se a função y = f(x) pode ser escrita na forma f(x) = ax + b +g(x), onde g(x) é uma função que
tende a zero, quando x então y = ax + b é uma assíntota oblíqua à curva que representa f(x)
1
Ex.: y x
x
1
lim x x
x
não tem assíntotas horizontais
1
lim x x
x
1
lim x 0
x
x
x = 0 é assíntota vertical
1
lim x 0
x
x
f ( x) 1
y = ax + b a lim x lim x 1 1
x x2
1
b lim x ( f ( x) ax) lim x 1 1 x 0
x
y = x é assíntota oblíqua
19. ANÁLISE DE FUNÇÕES
Para analisarmos uma função y = f(x) devemos determinar, se possível:
(i) o domínio da função;
(ii) as interseções do gráfico de f com os eixos coordenados;
(iii) a paridade e periodicidade de f;
(iv) o comportamento de f nos pontos de descontinuidade e nas fronteiras de seu domínio;
(v) o comportamento de f no infinito (- e + );
(vi) os intervalos em que f é crescente ou decrescente e os máximos e mínimos de f;
(vii) os intervalos de concavidade da curva que representa f e seus pontos de inflexão;
(viii) as assíntotas das curvas que representam f;
(ix) o esboço do gráfico de f
EXERCÍCIOS PROPOSTOS
1) Determine as derivadas das funções abaixo:
a) y = f(x)g(x)
b) y = x k , k R
2) Determine as derivadas das funções abaixo:
a) y = tan x f) y = arccos x
b) y = cot x g) y = arctan x
c) y = sec x h) y = arccot x
d) y = csc x i) y = arcsec x
e) y = arcsen x j) y = arccsc x
3) Determine as derivadas das funções abaixo:
2
x 2
a) y = e . cos x
b) y = 5
sen4 x
c) y = ln( x 1 x2 )
d) y = arcsen x3
e) y = ln (cos 3x)
f) y = arctan e 2x

12. g) y = (x3 +11) 15
2
h) y =
3
x 3 13
i) y = arcsec x 4
j) y = ln(ln(ln x))
cos(sen x )
k) y = sen2x + cos2x + arccos x ln 3 11
4) Calcule f’(4), se f(x) = arctan x sen(sen(sen ( x 4)))
5) Calcule f’( ), se f(x) = (tan x ) ln x
4
3
6) Ache um valor aproximado de 8,0857 .
7) Ache as derivadas enésimas das funções abaixo:
a) y = 1/x 1
b) y = sen x d) y =
1 2x
c) y = ln(1 + x)
4
e) y = sen x cos 4 x
8) Ache as derivadas das funções abaixo:
a) x10 – y10 + ln(x.y) = 0 y
b) x.sen y – cos y + cos 2y = 0 d) ln x2 y2 arctan
x
c) y = cos(x + y)
n 1
9) Ache a derivada enésima das função y = x . ln x
10) Uma bola de neve é formada de tal maneira que seu volume aumenta na razão de 8dm3/min. Com que
razão o raio é aumentado quando a bola tem 4dm de diâmetro?
11) Um tanque tem a forma de um cone invertido tendo uma altura de 5m e raio da base de 1m. O tanque se
enche de água a razão de 2m3/min. Com que velocidade sobe nível da água, quando a mesma está a 3m de
profundidade?
12) A altura de um certo cilindro circular está aumentando a uma razão de 3cm/min e o raio da base está
decrescendo a razão de 2cm/min. Determine a razão segundo a qual o volume do cilindro está variando quando
a altura é de 10cm e o raio da base é 4cm.
13) Calcule os limites abaixo:
tan(x / 4) f) lim x (e3x 5x)1 / x
a) lim x /4
x /4
2 g) lim x 0 (sen x)1 / ln x
( x 1)
b) lim x 1 x
2
1 cos x 2 4/ x
4
h) lim ((cos x ).e )
ex
sen x 1 x 0
c) lim x 0 x
ln(1 x) i) lim x 0 tan
1 cos6 x 2 x
d) lim x 0
1 cos3x j) lim x 0 x x
1
e) lim x 1 x1 x
12

13. 14) Achar os pontos críticos das funções abaixo:
a) y = x4 2 x2 2x 4
b) y = x3 h) y
3 2 3x 2 4x 5
c) y = 1 – x
3 i) y 2 tan x tan2 x , x [0, /2]
d) y = x
j) y = xx
e) y = ex
2
k) y arctan x ln 1 x2
f) y e x
g) y = x3 – 6x2 + 9x – 1 3
l) y x3
x
m) y = 2.sen x + cos 2x , x (0, )
15) Uma lata de forma cilíndrica deve conter um certo volume V. Quais são as dimensões de uma tal lata que
gaste a menor quantidade possível de material para ser feita.
16) A seção reta de um túnel tem a forma de um retângulo encimado por um semicírculo. O perímetro da seção
é igual a 18m. Determine o raio do semicírculo para que a área da seção seja máxima.
17) Um grande vidro plano de comprimento L, deve passar em pé por um canto retangular de um corredor,
passando de uma parte de largura a para outra de largura b. Qual o comprimento L máximo que o vidro pode
ter para que a manobra seja possível.
18) Qual deve ser a inclinação de um telhado, que proteja um vão de amplitude A, para que a água permaneça
no mesmo o menor tempo possível ?
19) Corta-se um pedaço de arame de comprimento L em duas partes. Com uma faz-se um círculo com a outra
um quadrado. Em que ponto deve-se cortar o arame para que a soma das áreas compreendidas pelas duas figuras
seja máxima ?
20) Um cartaz deve conter 50cm2 de matéria impressa com duas margens de 4cm cada em cima e em baixo e
duas margens laterais de 2cm cada. Determine as dimensões externas do cartaz de modo que sua área seja
mínima.
21) Use o princípio de Fermat: “ A luz caminha de um ponto A para outro ponto B segundo uma trajetória
que torna mínimo o tempo de percurso ” ; para demonstrar a Lei da refração de Snell-Decartes.
22) Um quadrilátero tem três lados congruentes de comprimento igual a 8. Determine o comprimento do
quarto lado que maximize a área.
23) Achar os intervalos de concavidade e os pontos de inflexão das funções abaixo:
a) y x3 6x2 12x 4 d) y (1 x2 )e x
b) y x sen x 3
e) y 4 x3 12x
2
c) y x ln x
24) Analise as funções abaixo:
a) y x 4 5x2 4
x2 x 1 3 2
b) y c) y x (6 x )
2
x x 1
d) y 2 ( x 1) x2 ( x 1) e) xy3 y 4 0
f) x3 y3 3x2

14. EXERCÍCIOS SUPLEMENTARES
1) Determine as derivadas das funções abaixo:
1 x x2 1
a) y = j) y = arcsen
1 x x2
sen x cos x 1 2
b) y = k) y = ln arcsen x + ln x + arcsen ln x
sen x cos x 2
c) y = 2x.sen x – (x2 – 2).cos x l) y = (cos x) sen x
x
d) y = x.cot x 1
e) y = ln x. log x – ln a.log a x m) y = 1
x
x2 sen x
f) y =
ln x n) y = x x
g) y = (a 2/3 – x2/3) 3/2 o) y = x x
h) y = ln x 1 ln( x 1) x x
p) y = x
m
a bxn 1 sen x
i) y = q) y = ln 2 arctan sen x
a bxn 1 sen x
f ' (1) f ' ' (1) f ' ' ' (1) f ( n) (1)
2) Sendo f(x) = x n, calcule: S = f(1) + 
1! 2! 3! n!
3) Verifique se a função y = cos ex + sen ex é solução da equação diferencial
y’’ – y’ + y.e2x = 0
4) Calcule y’’, sendo y = sen(x + y)
5) Dois navios A e B navegam a partir do ponto O segundo rotas que formam ângulo AÔB =120º. Com que
velocidade estão se separando os dois navios quando
OA = 8 milhas e OB = 6 milhas. Sabendo-se que A navega a 20 milhas/hora e
B a 30 milhas/h
6) Seja um círculo C de raio R e centro O. Imagine um motociclista, a noite, correndo ao longo de C no
primeiro quadrante, em direção a origem. Considere o ponto no eixo do x, iluminado pelo farol da motocicleta.
Determine a velocidade com esse ponto se aproxima da origem em função de R, S e v, onde S é a distância
da origem à motocicleta, tomada ao longo de C, v é a velocidade da motocicleta.
sen 3x a.sen 2 x b.sen x
7) Sabendo que lim x 0 existe e é finito, determine o valor numérico desse
x5
limite, sendo a e b constantes reais
8) A tangente traçada pelo ponto A a um círculo de raio r tem marcado um segmento AN de mesmo tamanho
que o arco AM. A reta MN corta o prolongamento do diâmetro AO no ponto B. Determine OB , em função
de r e AÔM e calcule lim AOM 0 OB
ˆ
9) Achar os pontos críticos das funções abaixo:
( x 2) (8 x) d) y = x – ln (1 + x)
a) y
x 2 ex
e) y
x
b) y = 3 (x 2 1) 2
c) y 2 sen 2 x sen 4 x
14

15. 10) Uma lâmpada pende sobre o centro de uma mesa redonda de raio r. A que altura da mesa deve esta a
lâmpada para que a iluminação de um objeto que se encontra a beira da mesa seja a melhor possível?
(A iluminação é diretamente proporcional ao cosseno do ângulo de incidência dos raios luminosos e
inversamente proporcional ao quadrado da distância ao foco )
11) Determine o ponto da curva y = x mais próximo do ponto (c, 0)
12) De um tronco redondo de diâmetro d deve-se cortar uma viga de seção retangular. Quais deverão ser a
largura x e altura y desta seção para que a viga tenha resistência máxima possível:
a) na compressão ?
b) na flexão ?
Obs.: Na resistência da viga à compressão é proporcional à área de sua seção transversal e a resistência a flexão
é proporcional ao produto da largura desta seção pelo quadrado de sua altura.
13) Analise as funções abaixo:
a) y x e1 / x e) y x2 (1 x)3
b) y x arctanx x2
2
c) y x ln x f) y ex 1
d) y xx
RESPOSTAS
EXERCÍCIOS PROPOSTOS
g ( x) f ' ( x)
1) a) y’ = g ' ( x) ln f ( x) f ( x) g ( x )
f ( x)
b) y’ = k x k 1
2) a) y’ = sec2 x g) y’ =
1
b) y’ = csc x 2 1 x2
c) y’ = sec x tan x 1
h) y’ =
d) y’ = cscx cot x 1 x2
1 1
e) y’ = i) y’ =
1 x2 x x2 1
1 1
f) y’ = j) y’ =
1 x2 x x2 1
2
3) a) y’ = 2xe x (cosx 2 sen x 2 )
4 cos x
b) y’ =
55 sen x
1
c) y’ =
2
1 x
3x 2
d) y’ =
1 x6
e) y’ = 3 tan 3x
2e 2 x
f) y’ =
1 e4x

16. g) y’ = 45 x 2 ( x 3 11)14
2x 2
h) y’ =
( x 3 13)3 x 3 13
4
i) y’ =
x x8 1
1
j) y’ =
x ln x ln(ln x)
1 cos(sen x )
k) y’ = ln cos x sen(sen x)
2 x(1 x)
4) 21/20
5) 2 ln
4
6) 2,0071
( n) ( 1)n n! ( n) 2n.n!
7) a) y d) y
xn 1 (1 2 x) n 1
n n
b) y ( n ) sen(x ) e) y ( n) 4n 1(cos(4 x ))
2 2
( n) ( 1) n 1(n 1)!
c) y
(1 x) n
10 sen(x y )
y(10 x 1) c) y '
8) a) y'
x (10 y
10
1) 1 sen(x y )
sen y x y
b) y ' d) y'
2 sen 2 y x cos y sen y x y
(n 1)!
9) y ( n)
x
10) 0,16 dm/min
11) 1,77 m/min
12) - 351,7 cm3/min
13) a) 1 f) e3
b) 2/ 2 g) e
c) 2 h) e-1/3
d) 4 i) 1
e) 1/e j) 1
16

17. EXERCÍCIOS SUPLEMENTARES
2) 2 n
y
4) y ' '
(1 cos(x y))3
5) 42,7 milhas/h
v
6)
S
1 cos
R
7) 1
8) 2r
9) a) ymax. = 9/16 quando x = 3,2
b) ymax. = 1 quando x = 0
3 1 3 1
c) ymin 3 , quando x = k e ymin 3 , quando x = k ;k
2 6 2 6
d) ymin = 0, quando x = 0
e) ymin = e, quando x = 1
10) r / 2
2c 1 2c 1
11) ,
2 2
d
12) a) x y
2
d 2
b) x e y d
3 3