Limite da função 1/x com x a tender para +/- infinito.

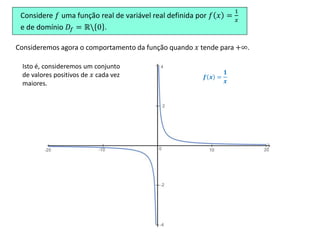
1. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒇 𝒙 =
𝟏
𝒙
Consideremos agora o comportamento da função quando 𝑥 tende para +∞.
Isto é, consideremos um conjunto
de valores positivos de 𝑥 cada vez
maiores.

2. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
𝒙 𝒇(𝒙)
1 1
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

3. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

4. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

5. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
4 0,25
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

6. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
4 0,25
10 0,1
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

7. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
4 0,25
10 0,1
20 0,05
𝑥
𝑓(𝑥)
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

8. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
4 0,25
10 0,1
20 0,05
50 0,02
100 0,001
1000 0,0001
𝑥
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

9. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
1 1
2 0,5
3 0,33(3)
4 0,25
10 0,1
20 0,05
50 0,02
100 0,001
1000 0,0001
… …
𝒙 → +∞ 𝒇(𝒙) → 𝟎
Quanto maior for o valor de 𝑥 , 𝑓(𝑥) aproxima-se
cada vez mais de zero. Isto é, quando
𝒙 𝐭𝐞𝐧𝐝𝐞 𝐩𝐚𝐫𝐚 + ∞, 𝒇(𝒙) tende para 𝟎.
Significa que o limite da função 𝑓 ,
quando 𝑥 tende para +∞, tende para 0.
Simbolicamente:
𝐥𝐢𝐦
𝒙→+∞
𝟏
𝒙
= 𝟎
𝑓(𝑥)
𝑥
𝒇 𝒙 =
𝟏
𝒙
Consideremos um conjunto de
valores positivos de 𝑥 cada vez
maiores.

10. Considere 𝑓 uma função real de variável real definida por 𝑓 𝑥 =
1
𝑥
e de domínio 𝐷𝑓 = ℝ 0 .
𝒙 𝒇(𝒙)
−1 −1
−2 −0,5
−3 −0,33(3)
−4 −0,25
−10 −0,1
−20 −0,05
−50 −0,02
−100 −0,001
−1000 −0,0001
… …
𝒙 → −∞ 𝒇(𝒙) → 𝟎
𝒇 𝒙 =
𝟏
𝒙
Quanto menor for o valor de 𝑥 , 𝑓(𝑥) aproxima-se
cada vez mais de zero. Isto é, quando
𝒙 𝐭𝐞𝐧𝐝𝐞 𝐩𝐚𝐫𝐚 − ∞, 𝒇(𝒙) tende para 𝟎.
O mesmo se aplica quando o valor
de 𝑥 tende para −∞.
O limite da função 𝑓, quando 𝑥 tende
para −∞, tende para 0:
𝐥𝐢𝐦
𝒙→−∞
𝟏
𝒙
= 𝟎
𝑥
𝑓(𝑥)