Sistem persamaan linier (SPL) merupakan persamaan-persamaan yang menghubungkan variabel-variabel tak diketahui dengan koefisien-koefisien yang diketahui. SPL dapat disajikan dalam bentuk matriks dan diselesaikan dengan metode eliminasi Gauss atau Gauss-Jordan. Metode-metode tersebut mengubah matriks SPL menjadi bentuk echelon-baris tereduksi untuk memperoleh penyelesaian SPL.

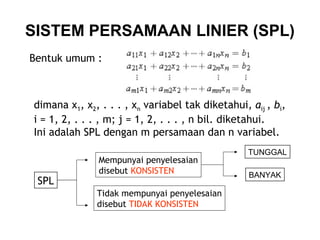
1. SISTEM PERSAMAAN LINIER (SPL)
Bentuk umum :
dimana x1, x2, . . . , xn variabel tak diketahui, aij , bi,
i = 1, 2, . . . , m; j = 1, 2, . . . , n bil. diketahui.
Ini adalah SPL dengan m persamaan dan n variabel.
SPL
Mempunyai penyelesaian
disebut KONSISTEN
Tidak mempunyai penyelesaian
disebut TIDAK KONSISTEN
TUNGGAL
BANYAK

2. ILUSTRASI GRAFIK
• SPL 2 persamaan 2 variabel:
• Masing-masing pers berupa garis lurus. Penyelesaiannya
adalah titik potong kedua garis ini.
kedua garis sejajar
kedua garis berpotongan kedua garis berhimpitan

3. PENYAJIAN SPL DALAM MATRIKS
SPL
BENTUK MATRIKS
STRATEGI MENYELESAIKAN SPL:
mengganti SPL lama menjadi SPL baru yang mempunyai
penyelesaian sama (ekuivalen) tetapi dalam bentuk yang
lebih sederhana.

4. TIGA OPERASI YANG MEMPERTAHANKAN
PENYELESAIAN SPL
SPL
1. Mengalikan suatu persamaan
dengan konstanta tak nol.
MATRIKS
1. Mengalikan suatu baris
dengan konstanta tak nol.
2. Menukar posisi dua
persamaan sebarang.
2. Menukar posisi dua baris
sebarang.
3. Menambahkan kelipatan suatu
persamaan ke persamaan
lainnya.
3. Menambahkan kelipatan suatu
baris ke baris lainnya.
Ketiga operasi ini disebut OPERASI BARIS ELEMENTER (OBE)
SPL atau bentuk matriksnya diolah menjadi bentuk sederhana sehingga tercapai 1 elemen tak nol pada suatu baris

5. CONTOH
DIKETAHUI
…………(i)
…………(ii)
…………(iii)
kalikan pers (i)
dengan (-2), kemudian tambahkan ke
pers (ii).
kalikan baris (i)
dengan (-2), lalu
tambahkan ke
baris (ii).
kalikan pers (i)
dengan (-3), kemudian tambahkan ke
pers (iii).
kalikan baris (i)
dengan (-3), lalu
tambahkan ke
baris (iii).
kalikan pers (ii)
dengan (1/2).
kalikan baris (ii)
dengan (1/2).

6. LANJUTAN CONTOH
kalikan pers (ii)
dengan (1/2).
kalikan baris (ii)
dengan (1/2).
kalikan pers (ii)
dengan (-3), lalu
tambahkan ke pers
(iii).
kalikan brs (ii)
dengan (-3),
lalu tambahkan
ke brs (iii).
kalikan pers (iii)
dengan (-2).
kalikan brs (iii)
dengan (-2).
kalikan pers (ii)
dengan (-1), lalu
tambahkan ke pers
(i).
kalikan brs (ii)
dengan (-1), lalu
tambahkan ke brs
(i).

7. Lanjutan CONTOH
kalikan pers (ii)
dengan (-1), lalu
tambahkan ke pers
(i).
kalikan pers (iii)
dengan (-11/2), lalu
tambahkan ke pers (i)
dan kalikan pers (ii) dg
(7/2), lalu tambahkan
ke pers (ii)
kalikan brs (ii)
dengan (-1), lalu
tambahkan ke brs
(i).
kalikan brs (iii)
dengan (-11/2), lalu
tambahkan ke brs (i)
dan kalikan brs (ii) dg
(7/2), lalu tambahkan
ke brs (ii)
Diperoleh penyelesaian x = 1, y = 2, z = 3. Terdapat
kaitan menarik antara bentuk SPL dan representasi
matriksnya. Metoda ini berikutnya disebut dengan
METODA ELIMINASI GAUSS.
KERJAKAN EXERCISE SET 1.1

8. BENTUK ECHELON-BARIS
Misalkan SPL disajikan dalam bentuk matriks berikut:
maka SPL ini mempunyai penyelesaian x = 1, y = 2, z = 3.
Matriks ini disebut bentuk echelon-baris tereduksi.
Untuk dapat mencapai bentuk ini maka syaratnya adalah sbb:
1. Jika suatu brs matriks tidak nol semua maka elemen
tak nol pertama adalah 1. Brs ini disebut mempunyai leading 1.
2. Semua brs yg terdiri dari nol semua dikumpulkan di bagian bawah.
3. Leading 1 pada baris lebih atas posisinya lebih kiri daripada leading
1 baris berikut.
4. Setiap kolom yang memuat leading 1, elemen lain semuanya 0.

9. Bentuk echelon-baris dan echelon-baris tereduksi
Matriks yang memenuhi kondisi (1), (2), (3) disebut
bentuk echelon-baris.
CONTOH bentuk echelon-baris tereduksi:
CONTOH bentuk echelon-baris:

10. Bentuk umum echelon-baris
dimana lambang ∗ dapat diisi bilananga real sebarang.

11. Bentuk umum echelon-baris tereduksi
dimana lambang ∗ dapat diisi bilananga real sebarang.

12. Penyelesaian SPL melalui bentuk echelon-baris
Misal diberikan bentuk matriks SPL sbb:
Tentukan penyelesaian masing-masing SPL di atas.

13. METODA GAUSS-JORDAN
Ide pada metoda eliminasi Gauss adalah mengubah
matriks ke dalam bentuk echelon-baris tereduksi.
CONTOH: Diberikan SPL berikut.
Bentuk matriks SPL ini adalah:

14. -2B1 + B2B2
5B2+B3  B3
B4 B4+4B2 1 3 - 2 0 2
0 0
0 0 - 1 - 2 0 - 3 - 1


0 0 0 0 0 0 0 


0 0 4 8 0 18 6 

B3 ⇄ B4
B3 B3/3
-3B3+B2B2
2B2+B1B1

15. Akhirnya diperoleh:
Akhirnya, dengan mengambil x2:= r, x4:= s dan x5:= t maka diperoleh
penyelesaian:
dimana r, s dan t bilangan real sebarang. Jadi SPL ini mempunyai tak
berhingga banyak penyelesaian.

16. METODA SUBSTITUSI MUNDUR
Misalkan kita mempunyai SPL dalam matriks berikut:
Bentuk ini ekuivalen dengan:
LANGKAH 1: selesaikan variabel leading, yaitu x6. Diperoleh:
LANGKAH 2: mulai dari baris paling bawah subtitusi ke atas, diperoleh

17. LANJUTAN SUBSTITUSI MUNDUR
LANGKAH 3: subtitusi baris 2 ke dalam baris 1, diperoleh:
LANGKAH 4: Karena semua persamaan sudah tersubstitusi maka pekerjaan substitusi selesai. Akhirnya dengan mengikuti langkah pada
metoda Gauss-Jordan sebelumnya diperoleh:

18. Eliminasi Gaussian
Mengubah menjadi bentuk echelon-baris (tidak perlu direduksi), kemudian
menggunakan substitusi mundur.
CONTOH: Selesaikan dengan metoda eliminasi Gaussian
PENYELESAIAN: Diperhatikan bentuk matriks SPL berikut:
Dengan menggunakan OBE diperoleh bentuk echelon-baris berikut:

19. • Kerjakan Exercise set 1.2 No. 1 – 11.

20. SPL HOMOGEN
• Bentuk umum:
• Penyelesaian trivial (sederhana):
• Bila ada penyelesaian lain yang tidak
semuanya nol maka disebut penyelesaian
taktrivial.

21. pasti ada penyelesaian trivial
SPL HOMOGEN
atau
penyelesaian trivial +
takberhingga banyak
penyelesaian taktrivial
ILUSTRASI:

22. Syarat cukup SPL homogen
mempunyai penyelesaian taktrivial
• Bila banyak variabel n lebih dari banyak
persamaan m maka SPL homogen
mempaunyai penyelesaian taktrivial.
• CONTOH:
# variabel = 5
# persamaan = 4.
• Bentuk matriks:

23. Bentuk akhir echelon-baris tereduksi:
PENYELESAIAN UMUMNYA :
x1 = − s − t , x2 = s, x3 = −t , x4 = 0, x5 = t.
dimana penyelesaian trivialnya terjadi pada saat s=t=0.
• Proses OBE dalam untuk menghasilkan bentuk
echeleon-baris tereduksi tidak mempengaruhi kolom
akhir matrik.
• Bila banyak persamaan awal n maka banyak pers. akhir
r tidak melebihi n, yaitu r ≤ n.

24. PENYELESAIAN SPL PADA
KOMPUTER
• Software komputasi yg dilengkapi alat
(tool) untuk menyelesaikan SPL:
– MATLAB, - MAPLE,
– MATHCAD, -MATHEMATICA, DLL.
• Umumnya menggunakan algoritma:
– Eliminasi Gauss, atau eliminasi Gauss-Jordan
• Prinsip penulisan program:
– menekan kesalahan pembulatan, minimalisasi
memori komputer, memaksimumkan speed.

25. SPL PADA MATLAB
• Diperhatikan SPL AX = b, mis A bujur
sangkar, i.e. #pers = #var.
• LANGKAH-LANGKAH:
– didefinisikan matriks A:
>>A=[a11 a12 a13; a21 a22 a23; a31 a32 a33]
– didefinisikan vektor ruas kanan b:
>>b=[b1;b2;b3]
– panggil penyelesaiannya:
>>X=Ab

26. • CONTOH: diperhatikan SPL
• Telah diketahui SPL ini mempunyai
penyelesaian
• Menggunakan MATLAB:
>> A=[1 1 2;2 4 -3;3 6 -5];
>> b=[9;1;0];
>>X=Ab
>>X =
1.0000
2.0000
3.0000
• Penyelsaian yang diperoleh sama dengan hasil
manual kita.

27. • Bila A invertibel, yaitu A-1 ada maka berlaku
AX = b
X = A-1b.
• Perintah pada MATLAB sbb:
>>X = inv(A)*b
X=
1.0000
2.0000
3.0000
• Bila A tidak mempunyai invers, SPL AX=b masih
memungkinkan penyelesaian. Akan dibahas
kelak.

28. Membentuk echelon-baris tereduksi
dengan MATLAB
>>A=[1 3 -2 0 2 0;2 6 -5 -2 4 -3;...
0 0 5 10 0 15;2 6 0 8 4 18];
>>b=[0;-1;5;6];
>>rref([A b])
ans =
1.0000
0
0
0
3.0000
0
0
0
0
1.0000
0
0
4.0000 2.0000
0
2.0000 0
0
0
0
1.0000
0
0
0
0
0
0.3333
0
Bandingkan dengan hasil yang sudah kita peroleh.

29. SPL tidak bujur sangkar
• Ubah menjadi bentuk echelon-baris
tereduksi dengan fungsi rref.
• Selesaikan dengan cara manual.
• CONTOH: diberikan SPL
• Dengan menggunakan rref pada
MATLAB diperoleh bentuk echelon-baris
sbb:

30. 1
0
0
-4
0
0
0
1
0
0
0
1
0
2
7
0
• Diperoleh x3 = 7, x2 = 2 dan x1 = -4.
• Bandingkan dengan hasil manual yang
sudah anda peroleh.
• SPL Homogen dilakukan dengan cara yang
sejalan.
TUGAS: Kerjakan Exercise 1.2 No. 12 s.d. 28

31. MATRIKS
• MATRIKS adalah array bilangan dalam
bentuk persegi panjang.
• CONTOH:

32. • Ukuran matriks ditentukan oleh banyak
baris dan banyak kolomnya. Matriks yang
mempunyai m baris dan n kolom
dikatakan berukuran m x n.
• Elemen pada baris ke i dan kolom ke j
matriks A ditulis aij. Bentuk umum:
atau
• Notasi lain elemen aij adalah

33. Matriks
mempunyai
Bentuk-bentuk matriks khusus:
1. Vektor baris: matriks dengan 1 baris,
Vektor kolom: matriks dengan 1 kolom.
2. Matriks bujursangkar:
banyak baris = kolom atau m=n.
Diagonal utama
d=[a11, a22, . . . ,ann]

34. OPERASI MATRIKS
• Dua matriks A dan B dikatakan sama, ditulis A=B jika
atau
• Jumlahan A+B matriks yang diperoleh dengan menjumlahkan elemen-elemen yang bersesuaian pada A dan B.
Dua matriks dapat dijumlahkan jika ukurannya sama.
DKL,
• Perkalian AB didefinisikan sbb:

35. Agar matriks A dan B dapat dikalikan maka haruslah
banyak kolom A sama dengan banyak baris B.