Apuntes del tema curvas cónicas de dibujo técnico de 2º de Bachillerato. España, 2013.

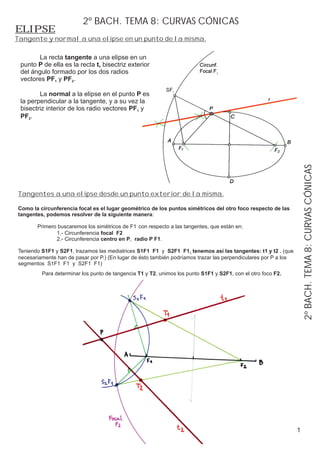
1. 2º BACH. TEMA 8: CURVAS CÓNICAS
ELIPSE
Tangente y normal a una elipse en un punto de la misma.
La recta tangente a una elipse en un
punto P de ella es la recta t, bisectriz exterior
del ángulo formado por los dos radios
vectores PF1 y PF2.
La normal a la elipse en el punto P es
la perpendicular a la tangente, y a su vez la
bisectriz interior de los radio vectores PF1 y
PF2.
2º BACH. TEMA 8: CURVAS CÓNICAS
Tangentes a una elipse desde un punto exterior de la misma.
Como la circunferencia focal es el lugar geométrico de los puntos simétricos del otro foco respecto de las
tangentes, podemos resolver de la siguiente manera:
Primero buscaremos los simétricos de F1 con respecto a las tangentes, que están en::
1.- Circunferencia focal F2
2.- Circunferencia centro en P, radio P F1.
Teniendo S1F1 y S2F1, trazamos las mediatrices S1F1 F1 y S2F1 F1,, tenemos así las tangentes: t1 y t2 . (que
necesariamente han de pasar por P.) (En lugar de ésto también podríamos trazar las perpendiculares por P a los
segmentos S1F1 F1 y S2F1 F1)
Para determinar los punto de tangencia T1 y T2, unimos los punto S1F1 y S2F1, con el otro foco F2.
1

2. Tangentes a una elipse paralelas a una dirección dada d.
Primero buscaremos los simétricos de F2 con respecto a las tangentes, que están en::
1.- Circunferencia focal F1.
2.- En la perpendicular la dirección dada ( eje de simetría)
Teniendo S1F2 y S2F2, resolvemos como en el caso anterior:
trazamos las mediatrices S1F2 F2 y S2F2 F2,, tenemos así las tangentes: t1 y t2 . (que necesariamente han de
ser paralelas a la dirección dada) (En lugar de ésto también podríamos trazar las perpendiculares por P a los segmentos
S1F2 F2 y S2F2 F2) S1F2
Para determinar los punto de tangencia T1 y T2, unimos
t1 los puntos S1F2 y S2F2,con el otro foco F1.
T1
t2
T2 S2F2 Puntos de intersección de
una recta con una elipse
Sabiendo que la elipse es el lugar geométrico de los puntos del plano que son centros de circunferencias que son
tangentes a una focal y pasan por el otro foco, el problema se resuelve a hallar los centros de estas
circunferencias. Así, buscaremos circunferencias tangentes a otra (circunferencia focal de F1 ) y que pasen por
dos puntos: F2 (o F1) y F´2 (el simétrico de F2 con respecto a la recta r.) Este problema lo resolvíamos por potencia.
Así: 1- Busco F´2, simétrico de F2 con respecto a la recta r.
2- Uniendo F´2 con F2 tengo eje radical
3- Dibujo la circunferencia focal de F1
4- Trazo una circunferencia auxiliar con centro en un punto de la mediatriz de F´2 F2 (línea de centros, que es la
recta r dada ) para hallar un eje radical con la circa focal de F1.
5- En el corte de los dos er, tenemos CR.
6- Hallamos k , con AC90º para el segmento CR F1 (o para CR Oaux).
7- Centro en CR, radio k, trazamos circa que corta a la focal en T1 y T2.
8- Uniendo T1 y T2 con F1 (centro de la focal F1), tenemos en la recta r dos puntos, I1 e I2, que serían centros de
circas que pasan por un foco y son tangentes al otro, por lo tanto, puntos de la elipse. Si son puntos de elipse, y están en r,
son los puntos de intersección de la recta con la elipse.
2

3. VALGAN LAS EXPLICACIONES ANTERIORES DE LA
ELIPSE, TENIENDO EN CUENTA LAS VARIACIONES DE
HIPÉRBOLA LOS ELEMENTOS QUE CONSTITUYEN LAS CURVAS
Tangente y normal a una HIPÉRbola en un punto de la misma.
Tangentes a una HIPÉRBOLA desde un punto exterior de la misma.
3

4. Tangentes a una HIPÉRBOLA paralelas a una dirección dada d.
2º BACH. TEMA 8: CURVAS CÓNICAS
Puntos de intersección de una recta con una HIPÉRBOLA
4

5. VALGAN LAS EXPLICACIONES ANTERIORES DE LA
PARÁBOLA ELIPSE, TENIENDO EN CUENTA LAS VARIACIONES DE
LOS ELEMENTOS QUE CONSTITUYEN LAS CURVAS
Tangente y normal a una PARÁbola en un punto de la misma.
2º BACH. TEMA 8: CURVAS CÓNICAS
Tangentes a una PARÁBOLA desde un punto exterior de la misma.
5

6. Tangentes a una PARÁBOLA paralelas a una dirección dada d.
Puntos de intersección de una recta con una PARÁBOLA
6

8. ELIPSE
La elipse es una curva cerrada y plana, cuyos puntos constituyen un lugar
geométrico que tiene la propiedad de que la suma de distancias de cada uno de sus puntos
a otros dos, fijos, F1 y F2, llamados focos, es constante e igual a 2a, siendo 2a la longitud del
eje mayor AB de la elipse.
Tiene dos ejes perpendiculares que se cortan en el punto medio O, centro de la
curva. El eje mayor AB se llama eje real y se representa por 2a. El eje menor CD se representa
por 2b. Los focos están en el eje real. La distancia focal F1 F2 se representa por 2c.
Entre a, b y c existe la relación: a2=b2+c2, por lo que: a = OA = F1 C (importante
para hallar los focos cuando se tienen eje mayor y menor)
La elipse es simétrica respecto de los dos ejes, y por lo tanto, respecto del centro O.
Las rectas que unen un punto M de la curva con los focos, se llaman radios vectores r1 y r2 y por la
definición se verifica: r1 + r2 =2a
La circunferencia principal, Cp, de la elipse es la que tiene por centro la elipse y
radio a. Se define como el lugar geométrico de los pies de las perpendiculares trazadas por
los focos a cada una de las tangentes.
Las circunferencias focales CF1 y CF2 de la elipse tienen por centro uno de los
focos y radio 2a. Son lugar geométrico de los simétricos del otro foco con respecto a las
tangentes.
La elipse se puede definir también como el lugar geométrico de los centros de
circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro
foco.

10. hipérbola
La hipérbola es una curva plana, abierta, con dos ramas; se define como el lugar
geométrico de los puntos cuya diferencia de distancias a otros dos, fijos, F y F’, llamados
focos, es constante e igual a 2a, siendo 2a la longitud del eje real AB de la hipérbola.
Tiene dos ejes perpendiculares que se cortan en el punto medio O, centro de la
curva. El eje AB se llama eje real y se representa por 2a. El eje CD se representa por 2b y se
llama imaginario porque no tiene puntos comunes con la curva. Los focos están en el eje real. La
distancia focal F-F’ se representa por 2c.
2 2 2
Entre a, b y c existe la relación: c =a +b por lo que c=OF=AD
La hipérbola es simétrica respecto de los dos ejes, y por lo tanto, respecto del centro
O. Las rectas que unen un punto T de la curva con los dos focos, se llaman radios vectores r1 y
r2 y por la definición se verifica: r2-r1=2a
La circunferencia principal Cp de la hipérbola es la que tiene por centro O y radio
a. Se define como el lugar geométrico de los pies de las perpendiculares trazadas por los focos a
cada una de las tangentes.
Las circunferencias focales CF1 y CF2 de la hipérbola tienen por centro uno de los
focos y radio 2a. Son lugar geométrico de los simétricos del otro foco con respecto a las tangentes.
La hipérbola se puede definir también como el lugar geométrico de los centros de
circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro
foco.
Las asíntotas de la hipérbola son las tangentes a la curva en los puntos del infinito. Estas
asíntotas son simétricas respecto de los ejes y pasan por el centro de la curva.

12. PARÁBOLA
La parábola es una curva plana, abierta y de una rama. Se define como el lugar
geométrico de los puntos del plano que equidistan de un punto fijo F, llamado foco, y de una
recta fija d, llamada directriz. Tiene un vértice V y un eje de simetría que pasa por V y por el
foco y es perpendicular a la directriz. La tangente en el vértice a la curva es paralela a la
directriz.
El vértice, como otro punto cualquiera, equidista de la directriz y del foco, es
decir, OA=AF=p/2. Los radios vectores del punto T son T SF y T F.
Se llama parámetro 2p de la parábola, al igual que en la elipse y en la hipérbola, a
la longitud de la cuerda que es perpendicular al eje en el foco.
La circunferencia principal Cp de la parábola, sería una recta, que es la tangente
en el vértice. Se define como el lugar geométrico de los pies de las perpendiculares trazadas por
los focos a cada una de las tangentes
La directriz d hace de circunferencia focal de F2. Es lugar geométrico de los
simétricos del otro foco (F) con respecto a las tangentes.
La parábola se puede definir también como el lugar geométrico de los centros de
circunferencias que pasan por un foco y son tangentes a la circunferencia focal del otro
foco.