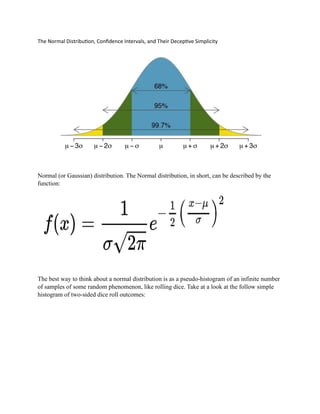
The Normal Distribution, Confidence Intervals, and Their Deceptive Simplicity
Normal (or Gaussian) distribution. The Normal distribution, in short, can be described by the
function:
The best way to think about a normal distribution is as a pseudo-histogram of an infinite number
of samples of some random phenomenon, like rolling dice. Take at a look at the follow simple
histogram of two-sided dice roll outcomes:

Take a look at the Normal distribution again, and take a guess at what the percents and symbols
mean:
z-score is the conversion of any data point into a format relative to its own standard deviation
and mean, this results in all z-scores falling into the same grand, relativized scope of comparison
via…

The Normal distribution!
This is wild and unintuitive. Truly.
Why in the world do z-scores, the simple act of converting data points into numbers by dividing
them by the standard deviation, have anything to do with the probability density function (PDF)
for the Normal distribution?
All I’ll say here, for the sake of brevity and simplicity, is that the Normal distribution
fundamentally involves circles and the fact that pi is the same for all circles, and that because the
act of creating a z-score involves squaring the difference of each data point from the mean, the
value of pi is implicitly involved in the standardization of all data sets through z-score
conversion.
Let’s finally look at how to construct a confidence interval.
The formula for a confidence interval
First, we decide what level of confidence we want our estimation to involve. The standard trio is
90%, 95%, and 99%. We then subtract this confidence from 100% and call it alpha, or α, after
converting into decimal format. So for a 95% CI, we have α =1.00 - .95 = .05. We then split α
into two: α/2, since our confidence interval will be symmetric around the presumed true mean:
.05/2 = .025. The standard Stats 101 strategy at this point is to look up this value in the
completely arcane table of High Magic, the dreaded z-table: