Componentes rectangulares

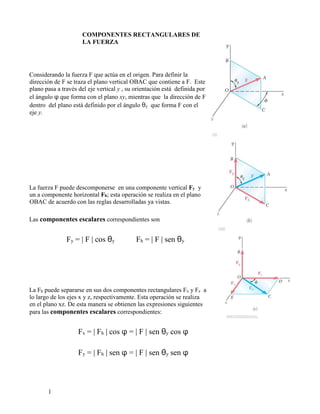
1. 1
COMPONENTES RECTANGULARES DE
LA FUERZA
Considerando la fuerza F que actúa en el origen. Para definir la
dirección de F se traza el plano vertical OBAC que contiene a F. Este
plano pasa a través del eje vertical y , su orientación está definida por
el ángulo φ que forma con el plano xy, mientras que la dirección de F
dentro del plano está definido por el ángulo θy que forma F con el
eje y.
La fuerza F puede descomponerse en una componente vertical Fy y
un a componente horizontal Fh; esta operación se realiza en el plano
OBAC de acuerdo con las reglas desarrolladas ya vistas.
Las componentes escalares correspondientes son
Fy = | F | cos θy Fh = | F | sen θy
La Fh puede separarse en sus dos componentes rectangulares Fx y Fz a
lo largo de los ejes x y z, respectivamente. Esta operación se realiza
en el plano xz. De esta manera se obtienen las expresiones siguientes
para las componentes escalares correspondientes:
Fx = | Fh | cos φ = | F | sen θy cos φ
Fy = | Fh | sen φ = | F | sen θy sen φ

2. 2
Aplicando el teorema de Pitágoras a los triángulos OAB y OCD (se omiten cálculos) se obtiene la
siguiente relación entre la magnitud de F y sus componentes rectangulares escalares
| F |= Fx2 +Fy2 +Fz2
la relación que existe entre la fuerza F y sus tres componentes Fx, Fy, y Fz se presenta más fácil si se
Con el uso de los vectores unitarios i, j y k dirigidos a lo largo de los ejes x, y y z respectivamente se
obtienen las componentes rectangulares de la fuerza:
Fx = | F | cos θx i Fy = | F | cos θy j Fz = | F | cos θz k
Conformando así la expresión vectorial de la fuerza
F = F x i + F y j + F z k
Cosenos directores ángulos directores
F
observa lo siguiente

3. 3
| F |
| F |
finalmente
F = | F | cos θx i + | F | cos θy j + | F | cos θz k
F = | F | (cos θx i + cos θy j + cos θz k )
F = | F | ef
donde ef = cos θx i + cos θy j + cos θz k
Ejemplo:
Si F = 500 N forma ángulos de 600
, 450
y 1200
con los ejes x, y y z
respectivamente. Encuentre las componentes Fx Fy y Fz de la fuerza.
cosθx
cosθy
cosθz
= x
| F |
F
= y
| F |
F
= z
F
θx =ang cos x
| F |
F
θy =ang cos y
| F |
F
θz =ang cos z

4. 4
Componentes esclares
Fx = F cos θx = 500 cos 60 = 250 N
Fy = F cos θy = 500 cos 45 = 353.55 N
Fz = F cos θz = 500 cos 120 = - 250 N
Componentes rectangulares
Fx = F cos θx i = 500 cos 60 = 250 N
Fy = F cos θy j = 500 cos 45 = 353.55 N
Fz = F cos θz k = 500 cos 120 = - 250 N
Expresión vectorial
F= 250 i + 353.55 j – 250 k [ N ]