1. ESTATICA

2. • Cuerpo Rígido
• Fuerza
• Tipos de Fuerza
• Primera Ley de Newton
• Tercera Ley de Newton
CONTENIDOS TEMÁTICOS

3. ESTATICA
Es la parte de la Mecánica que estudia la
estabilidad y equilibrio de los cuerpos.
CUERPO RIGIDO
Son cuerpos constituidos por un sistema de
partículas de manera que la distancia relativa
entre ellas no se altera bajo la acción de
fuerzas externas.

4. Concepto de Fuerza
• Es una interacción entre dos o más cuerpos. Una fuerza
puede causar un cambio en la velocidad, entonces,
podemos considerar que una fuerza es aquello que
ocasiona que un cuerpo acelere; y/o un cambio en la forma
del mismo.
• Si la fuerza neta ejercida sobre un cuerpo es cero la
aceleración de este es cero y su velocidad permanece
constante o ser nula.
Fuerza

5. TIPOS DE FUERZA
a)Fuerza de Contacto.- Aparecen cuando hay
contacto directo entre los cuerpos. Ejemplo: La fuerza
normal, las reacciones.
b)Fuerzas de Campo.-Estas fuerzas aparecen como
consecuencia de la interacción entre los cuerpos y no
necesariamente hay contacto entre los cuerpos.
Ejemplo: Fuerza gravitacional.

7. • La primera ley de Newton o ley del movimiento a
veces llamada ley de inercia establece que: “Un
cuerpo sobre el que no actúa una fuerza neta posee una
velocidad constante ( que puede ser cero ) y aceleración
nula”
• O también: “Todo cuerpo permanece en reposo
(velocidad igual a cero ) o con movimiento uniforme
rectilíneo (velocidad constante ) a menos que actúe una
fuerza que cambie su estado” (Ley de Inercia)
PRIMERA LEY DE NEWTON

8. Inercia.-nercia.- EEs la oposición que un cuerpo ofrece a
cambiar su estado de reposo o movimiento.
Masa.-Masa.- Es la medida cuantitativa de la inercia. La
masa es una propiedad inherente de un cuerpo y es
independiente del entorno del cuerpo y del método
empleado para medirlo. La masa no debe confundirse
con el peso. “Masa y peso son dos cantidades
diferentes”. El peso de un cuerpo es igual a la
magnitud de la fuerza gravitacional ejercida sobre el
cuerpo y varia con su ubicación.

9. LINEA DE ACCION Y PUNTO DE APLICACIÓNLINEA DE ACCION Y PUNTO DE APLICACIÓN
• Cuando una fuerza actúa sobre un cuerpo indeformable, se puede
desplazar libremente sobre su línea de acción, provocando el mismo
efecto, en consecuencia una fuerza puede ser aplicada en cualquier
punto a lo largo de su línea de acción, siempre y cuando se mantenga la
magnitud y sentido. Ejemplo:

10. TERCERA LEY DE NEWTON
Cuando un par de fuerzas que no son paralelas entre sí, que están
en un mismo plano y que actúan sobre un cuerpo sólido
indeformable, se puede comprobar, por lo indicado en el punto
anterior, que esas dos fuerzas pueden ser trasladadas a una
intersección común a lo largo de sus líneas de acciones.
Se puede comprobar que esas dos fuerzas actuando en el punto
de intersección de las líneas de acciones, son equivalentes a
una sola fuerza aplicada actuando en ese punto y cuyo valor
es

11. • La fuerza de acción es igual en magnitud a la fuerza de reacción y
opuesta en sentido. En todos los casos, las fuerzas de acción y
reacción actúan sobre objetos diferentes y deben ser del mismo
tipo.
m
1
m2
F12
F12
Esto significa que la fuerza que ejerce el cuerpo 1 sobre el cuerpo
2 (F12) es igual en módulo y dirección, pero de sentido opuesto a la
fuerza que ejerce el cuerpo 2 sobre el cuerpo 1 (- F 21).

13. EJEMPLOS DE APLICACIÓN
1.Un semáforo que pesa 125 N cuelga de un cable unidos a otros
dos cables sujetos a un soporte, como se ve en la figura. Los
cables superiores forman ángulos de 37º y 53 º con la horizontal
. Estos cables superiores no son tan fuertes como el cable
vertical, y se romperán si la tensión en ellos excede de 100 N
¿permanecerá el semáforo colgando en esta situación o se
romperá uno de los cables?.
= 125 N= 125 N
= 125 N= 125 N
Diagrama de
cuerpo libre.

14. Según el diagrama de cuerpo libre se
hace una descomposición de los vectores
y aplicamos la ley de Newton, ed.

15. 2. Una esfera de 180 kg se encuentra en equilibrio tal como se ve
en la figura. calcular la tensión en la cuerda y la reacción normal
de la pared.

16. Se desarrolla su DCL, ubicando las fuerzas en un plano cartesiano XY,
luego usar el triángulo notable de 37º, recordando la proporción que
existe entre sus lados.
Se desarrolla su DCL, ubicando las fuerzas en un plano cartesiano XY,
luego usar el triángulo notable de 37º, recordando la proporción que
existe entre sus lados.
T
W=180 x 10 = 1800 N
N
W = mg
37º
Recordando la
descomposición
Vectorial y ubicando
convenientemente el
triángulo se tiene.
W= 1800 N = 4k
N = 3k
T = 5k
37º
53º

17. Observamos que 4k=1800N, por lo tanto k=450N, luego
reemplazando en el triángulo Se tiene los valores de T y N.
T = 5k = 5 x 450 N = 2250 N
N = 3k = 3 x 450 N = 1350 N

18. 6.Determinar el valor absoluto y la dirección de la fuerza F2 de la
figura adjunta. Para que el bloque de 780N de peso se encuentre en
equilibrio si el modulo de la fuerza F1 es 460 N.

19. 
8,35386,1cot
386,1
47
47cos
460
780
cot
460
780
47coscot47
460
78047coscos47
460
780)47(
==→
=
−
=→=+→
=
+
→=
+
garc
sen
ggsen
sen
sensen
sen
sen
α
αα
α
αα
α
α
Reemplazando en la primera y la segunda ecuación
NF
sen
F
sen
575
478,35
460
2
2
=→=

20. 7.En el esquema de la figura, el bloque de peso P se mantiene en
equilibrio cuando se aplica una fuerza F=500N en el punto B del
sistemas de cables. Determinar las tensiones en los cables y el
peso P.

22. 0702030
0cos70cos20cos30cos
=−+−=
=−−+=
∑
∑
α
α
senFsenFsenFsenFF
FFFFF
ABDCy
ABDCx
Las componentes de la fuerza son
138.9787080020800301000
163.134470cos80020cos80030cos1000cos
=+−=
=−+=
sensensensenF
F
A
A
α
α

36727,0
163.1344
138.978
tan
4,1662)138.978()163.1344( 22
=→==
=+=
αα
AF
entonces

23. EJERCICIOS
1. Determinar las tensiones sobre
las cuerdas AC y BC . Si M
pesa 40 lb-f.
2. Determinar las tensiones sobre las
cuerdas AC y BC . Si M pesa 40 lb-f .
3.Encontrar la tensión en el cable y la
compresión en la varilla de las Figura
suponiendo que el peso suspendido sea en
todos los casos de 1000 N. Despréciese el peso
de la varilla.

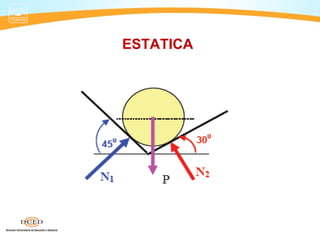
24. EJERCICIOS
4.Una esfera cuyo peso es
de 50 N descansa sobre
dos planos lisos, inclinados
respectivamente con
respecto a la horizontal,
ángulos de 300 y 450.
Calcular las reacciones de
los dos planos sobre la
esfera.

25. GRACIAS