Este documento describe el círculo trigonométrico y las funciones trigonométricas de los ángulos en los cuatro cuadrantes. Explica cómo calcular las funciones seno, coseno, tangente y cotangente para ángulos notables como 30°, 45° y 60° grados usando triángulos rectángulos y equiláteros. También cubre cómo reducir ángulos en el segundo y tercer cuadrante al primer cuadrante para calcular sus funciones trigonométricas.

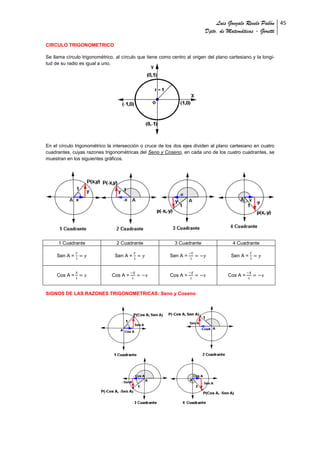
1. Luis Gonzalo Revelo Pabón 45
Dpto. de Matemáticas - Goretti
CIRCULO TRIGONOMETRICO
Se llama círculo trigonométrico, al círculo que tiene como centro al origen del plano cartesiano y la longi-
tud de su radio es igual a uno.
En el círculo trigonométrico la intersección o cruce de los dos ejes dividen al plano cartesiano en cuatro
cuadrantes, cuyas razones trigonométricas del Seno y Coseno, en cada uno de los cuatro cuadrantes, se
muestran en los siguientes gráficos.
1 Cuadrante 2 Cuadrante 3 Cuadrante 4 Cuadrante
Sen A = Sen A = Sen A = Sen A =
Cos A = Cos A = Cos A = Cos A =
SIGNOS DE LAS RAZONES TRIGONOMETRICAS: Seno y Coseno

2. Luis Gonzalo Revelo Pabón 46
Dpto. de Matemáticas - Goretti
Al analizar el desplazamiento del radio vector en cada uno de los cuatro cuadrantes, se deduce que el
signo de las funciones trigonométricas son las siguientes:
Función 1 Cuadrante 2 Cuadrante 3 Cuadrante 4 Cuadrante
Seno A + + - -
Coseno A + - - +
Tangente A + - + -
Ejemplo:
El Sen 30° es positivo y el Cos 30° es positivo.
El Sen 135° es positivo y el Cos 135° es negativo.
El Sen 225° es negativo y el Cos 225° es negativo.
El Sen 315° es negativo y el Cos 315° es positivo.
VALORES DE LOS ANGULOS CUADRANTALES
Función 0º 90º 180º 270º 360º
Seno 0 1 0 -1 0
Coseno 1 0 -1 0 1
Tangente 0 0 0
RAZONES TRIGONOMÉTRICAS DE LOS ÁNGULOS NOTABLES
Por definición se tiene que: La suma de los ángulos internos de un triángulo es igual a 180°.
CASO 1: Si a un cuadrado cuya longitud de sus lados es igual a la unidad (1), se traza una diagonal,
entonces observamos que se genera dos triángulos rectángulos, con un ángulo de 90° y dos ángulos de
45°, en cada uno de ellos.
Caso 2: Si a un triángulo equilátero cuya longitud de sus lados es igual a dos (2), entonces sus tres ángu-
los tienen una magnitud de 60°. Ahora al trazar la altura del triángulo de uno de sus vértices, da origen
de dos triángulos rectángulos, donde cada uno de los triángulos tiene un ángulo de 90°, uno de 60° y otro
de 30°. A los ángulos de 30°, 45° y 60° se les llama ángulos notables.
CASO 1: FUNCIONES TRIGONOMÉTRICAS PARA EL ÁNGULO DE 45°
Para encontrar las funciones trigonométricas de un ángulo de 45°, se utiliza como referencia un cuadrado
de lado igual a uno. Así:
Al cuadrado de la figura se traza una diagonal, de tal manera que el cuadrado queda dividido en dos
triángulos rectángulos, donde los valores de los catetos es igual a 1, y el valor de la hipotenusa es igual a
√ , cuyo valor es obtenido aplicando el teorema de Pitágoras así:
√

3. Luis Gonzalo Revelo Pabón 47
Dpto. de Matemáticas - Goretti
De esta manera, encontramos las funciones trigonométricas para el ángulo de 45°.
√ √ √ √
Sen 45º = Cos 45º = Tag 45º =
√ √ √ √ √ √
CASO 2: FUNCIONES TRIGONOMÉTRICAS PARA LOS ÁNGULOS DE 30° Y 60°
Para hallar las funciones trigonométricas de los ángulos de 30° y 60° grados, tomamos un triángulo equi-
látero, cuyos lados tienen una longitud igual de 2 unidades.
Ahora, tomemos como punto de referencia al triángulo equilátero DBC, y desde el ángulo C que tiene
una magnitud angular de 60º grados, bajamos una bisectriz y observamos que el ángulo C se divide en
dos ángulos iguales de 30º grados cada uno y el triángulo equilátero DBC, se ha dividido en dos triángu-
los rectángulos siendo uno de ellos el triángulo ABC, cuya altura de este triángulo es ̅̅̅̅.
Para encontrar las funciones trigonométricas de los ángulos de 30° y 60° (ángulos A y B), en el triángulo
ABC, es necesario en primer lugar encontrar el valor de la altura ̅̅̅̅ del triángulo rectángulo, ya que lo
desconocemos. Para ello aplicamos el teorema de Pitágoras, así:
√
Ahora, como ya conocemos los valores de los catetos y de la hipotenusa del triángulo ABC, entonces sí
podemos encontrar los valores de las funciones trigonométricas para los ángulos de 30º y 60º, así:
√ √ √
Sen 30º = Cos 30º Tag 30º =
√ √ √
√ √
Sen 60º = Cos 60º = Tag 60º = √
Resumiendo en un cuadro general las funciones trigonométricas para los Ángulos Notables de 30°, 45°
y 60°, tenemos:
Función 30º 45º 60º
Seno
√ √
Coseno
√ √
√
Tangente √

4. Luis Gonzalo Revelo Pabón 48
Dpto. de Matemáticas - Goretti
COFUNCION: Es una función trigonométrica donde a los ángulos de 90º grados y 270º grados al aumen-
tarles o disminuirles un ángulo A, es decir (90º , entonces la función trigonométrica es
sustituida por otra función trigonométrica. Así:
FUNCION Seno Coseno Tangente Cotangente Secante Cosecante
COFUNCION coseno Seno Cotangente Tangente Cosecante Secante
REDUCCIÓN DE ÁNGULOS AL PRIMER CUADRANTE.
Dado un ángulo (d), que se encuentre ubicado en el segundo, tercero o cuarto cuadrante del plano carte-
siano, es posible encontrar un ángulo (A), que se encuentra en el primer cuadrante, de tal manera que
las razones trigonométricas para los dos ángulos (d) y (A) sean iguales.
1 CASO: REDUCCION DE ANGULOS DEL SEGUNDO CUADRANTE AL PRIMERO.
Parte 1: “Si nos dan un ángulo (d), que se encuentra ubicado en el segundo cuadrante de un plano car-
tesiano, entonces el ángulo dado (d) es igual, a 90º grados más un ángulo (A) que se encuentra en el
primer cuadrante”, es decir: d = 90º +A, entonces el ángulo del primer cuadrante será igual a:
A = d – 90º
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se ubica en el se-
gundo cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está ubicado en el primer
cuadrante, se debe aplicar las siguientes ecuaciones:
Sen (d) = Sen (90º + A) = Cos A
Cos (d) = Cos (90º + A) = - Sen A
Tang (d) = tang (90º + A) = - Cotag A
Cotag (d) = Cotag (90º + A) = - Tang A
Nota:
Tang (d) = = - Cotag A
Cotag (d) = = - tang A
Parte 2: “Si nos dan un ángulo (d), que se encuentra ubicado en el segundo cuadrante de un plano car-
tesiano, entonces el ángulo dado (d) es igual a 180º menos el ángulo (A) del primer cuadrante”, es decir
d= 180º - A, entonces el ángulo del primer cuadrante será igual a: A = 180º- d

5. Luis Gonzalo Revelo Pabón 49
Dpto. de Matemáticas - Goretti
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se halla en el se-
gundo cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está en el primer cuadran-
te, se debe aplicar las siguientes ecuaciones:
Sen (d) = Sen (180º - A) = Sen A
Cos (d) = Cos (180º - A) = - Cos A
Tang (d) = Tang (180º - A) = - tang A
Cotag (d) = Cotag (180º - A) = - Cotag A.
Nota:
Tang (d) = = - tang A
Cotag (d) = = - Cotag A
Ejemplos:
Determine las razones trigonométricas seno, coseno, tangente y cotangente, para los ángulos de a) 120º,
b) 135º.
a) Solución para el ángulo de 120º
Primera forma de resolverlo:
El ángulo dado es d= 120º pero d = 90º +A
120º = 90º +A, entonces A = 120º - 90º = 30º
Sen (d) = Sen (90º + A) = Cos A remplazamos
Sen 120º = Sen (90º + 30º) = Cos 30º =0, 8660
Cos (d) = Cos (90º + A) =- Sen A remplazamos
Cos 120º = Cos (90º +30º) = - Sen 30º = - 0,5
Tang (d) = tang (90º + A) = - Cotag A remplazamos
Tang 120º = tang (90º+30º) = - Cotag 30º = - 1,732
Cotag (d) = Cotag (90º + A) = - Tang A remplazamos
Cotag 120º = Cotag (90º +30º) = - Tang 30º = - 0,5773
Segunda forma de resolverlo
El ángulo dado es d= 120º pero d = 180º - A
120º = 180º - A, entonces A = 180º - 120º = 60º
Sen (d) = Sen (180º - A) = Sen A remplazamos
Sen 120º = Sen (180º - 60º) = Sen 60º =0,8660
Cos (d) = Cos (180º - A) = - Cos A remplazamos
Cos 120º = Cos (180º - 60º) = - Cos 60º = -0,5
Tang (d) = Tang (180º- A) = - tang A remplazamos
Tang 120º = Tang (180º - 60º) = - tang 60 = - 1,7320
Cotag (d) = Cotag (180º - A) = - Cotag A remplazamos
Cotag 120º = Cotag (180º - 60º) = - Cotag 60º = -0,5773

6. Luis Gonzalo Revelo Pabón 50
Dpto. de Matemáticas - Goretti
b) Solución para el ángulo de 135º
Primera forma de resolverlo:
El ángulo dado es d= 135º pero d = 90º +A
135º = 90º +A, entonces A = 135º - 90º = 45º
Sen (d) = Sen (90º + A) = Cos A remplazamos
Sen 135º = Sen (90º + 45º) = Cos 45º = 0,7071
Cos (d) = Cos (90º + A) = - Sen A remplazamos
Cos 135º = Cos (90º +45º) = - Sen 45º = - 0,7071
Tang (d) = tang (90º + A) = - Cotag A remplazamos
Tang 135º = tang (90º+45º) = - Cotag 45º = - 1
Cotag (d) = Cotag (90º + A) = - Tang A remplazamos
Cotag 135º = Cotag (90º +45º) = - Tang 45º = - 1
Segunda forma de resolverlo
El ángulo dado es d= 135º pero d = 180º - A
135º = 180º - A, entonces A = 180º - 135º = 45º
Sen (d) = Sen (180º - A) = Sen A remplazamos
Sen 135º = Sen (180º - 45º) = Sen 45º = 0,7071
Cos (d) = Cos (180º- A) = - Cos A remplazamos
Cos 135º = Cos (180º - 45º) = - Cos 45º = - 0,7071
Tang (d) = Tang (180º - A) = - tang A remplazamos
Tang 135º = Tang (180º - 45º) = - tang 45º = -1
Cotag (d) = Cotag (180º - A) = - Cotag A remplazamos
Cotag 135º = Cotag (180º - 45º) = - Cotag 45º = -1
2 CASO: REDUCCION DE ANGULOS DEL TERCER CUADRANTE AL PRIMERO.
Parte 1: “Si nos dan un ángulo (d), que se encuentra ubicado en el tercer cuadrante de un plano carte-
siano, entonces el ángulo dado (d) es igual, a 180º más un ángulo (A) que se encuentra en el primer
cuadrante”, es decir: d = 180º +A, entonces el ángulo del primer cuadrante será igual a: A = d – 180º
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se ubica en el ter-
cer cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está en el primer cuadrante,
se debe aplicar las siguientes ecuaciones:

7. Luis Gonzalo Revelo Pabón 51
Dpto. de Matemáticas - Goretti
Sen (d) = Sen (180º + A) = - Sen A
Cos (d) = Cos (180º + A) = - Cos A
Tang (d) = tang (180º + A) = tang A
Cotag (d) = Cotag (180º + A) = Cotag A
Nota:
Tang (d) = = Tag A
Cotag (d) = = Cotag A
Parte 2: “Si nos dan un ángulo (d), que se encuentra ubicado en el tercer cuadrante de un plano carte-
siano, entonces el ángulo dado (d) es igual a 270º menos el ángulo (A) del primer cuadrante”, es decir
d= 270º - A, entonces el ángulo del primer cuadrante será igual a: A = 270º- d
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se ubica en el ter-
cer cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está en el primer cuadrante,
se debe aplicar las siguientes ecuaciones:
Sen (d) = Sen (270º - A) = - Cos A
Cos (d) = Cos (270º - A) = - Sen A
Tang (d) = Tang (270º - A) = Cotag A
Cotag (d) = Cotag (270º - A) = Tang A.
Nota:
Tang (d) = = Cotag A
Cotag (d) = = tag A
Ejemplos:
Determine las razones trigonométricas seno, coseno, tangente y cotangente, para los ángulos de a) 192º,
b) 255º.
a) Solución para el ángulo de 192º
Primera forma de resolverlo:
El ángulo dado es d= 192º pero d = 180º +A
192º = 180º +A, entonces A = 192º - 180º = 12º
Sen (d) = Sen (180º + A) = - Sen A remplazamos
Sen 192º = Sen (180º + 12º) = - Sen 12º = -0,2079

8. Luis Gonzalo Revelo Pabón 52
Dpto. de Matemáticas - Goretti
Cos (d) = Cos (180º + A) = - Cos A remplazamos
Cos 192º = Cos (180º + 12º) = - Cos 12º = -0,9781
Tang (d) = tang (180º + A) = tang A remplazamos
Tang 192º = tang (180º + 12º) = tang 12º = 0,2125
Cotag (d) = Cotag (180º + A) = Cotag A remplazamos
Cotag 192º = Cotag (180º + 12º) = Cotag 12º = 4,7046
Segunda forma de resolverlo
El ángulo dado es d= 192º pero d = 270º - A
192º = 270º - A, entonces A = 270º - 192º = 78º
Sen (d) = Sen (270º- A) = - Cos A remplazamos
Sen 192º = Sen (270º - 78º) = - Cos 78º = -0,2079
Cos (d) = Cos (270º - A) = - Sen A remplazamos
Cos 192º = Cos (270º - 78º) = - Sen 78º= -0,9781
Tang (d) = Tang (270º- A) = Cotag A remplazamos
Tang 192º = Tang (270º - 78º) = Cotag 78º= 0,2125
Cotag (d) = Cotag (270º - A) = Tang A. remplazamos
Cotag 192º = Cotag (270º - 78º) = Tang 78º= 4,7046
3 CASO: REDUCCION DE ANGULOS DEL CUARTO CUADRANTE AL PRIMERO.
Parte 1: “Si nos dan un ángulo (d), que se encuentra ubicado en el cuarto cuadrante de un plano carte-
siano, entonces el ángulo dado (d) es igual, a 270º más un ángulo (A) que se encuentra en el primer
cuadrante”, es decir: d = 270º +A, entonces el ángulo del primer cuadrante será igual a:A = d – 270º
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se halla en el cuarto
cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está en el primer cuadrante, se
debe aplicar las siguientes ecuaciones:
Sen (d) = Sen (270º + A) = - Cos A
Cos (d) = Cos (270º + A) = Sen A
Tang (d) = tang (270º + A) = - Cotag A
Cotag (d) = Cotag (270º + A) = - Tang A
Parte 2: “Si nos dan un ángulo (d), que se encuentra ubicado en el cuarto cuadrante de un plano carte-
siano, entonces el ángulo dado (d) es igual a 360º menos el ángulo (A) del primer cuadrante”, es decir
d= 360º - A, entonces el ángulo del primer cuadrante será igual a: A = 360º- d

9. Luis Gonzalo Revelo Pabón 53
Dpto. de Matemáticas - Goretti
Por lo tanto, para encontrar las funciones trigonométricas de un ángulo dado (d), que se halla en el cuarto
cuadrante de un plano cartesiano, para convertirlo a un ángulo (A) que está en el primer cuadrante, se
debe aplicar las siguientes ecuaciones:
Sen (d) = Sen (360º - A) = - Sen A
Cos (d) = Cos (360º - A) = Cos A
Tang (d) = Tang (360º - A) = - Tang A
Cotag (d) = Cotag (360º - A) = - Cotag A.
Nota:
Tang (d) = = - Tag A
Cotag (d) = = - tag A
Ejemplos:
Determine las razones trigonométricas seno, coseno, tangente y cotangente, para los ángulos de a) 349º,
b) 295º.
a) Solución para el ángulo de 349º
Primera forma de resolverlo:
El ángulo dado es d= 349º pero d = 270º +A
349º = 270º +A, entonces A = 349º - 270º = 79º
Sen (d) = Sen (270º + A) =- Cos A remplazamos
Sen 349º = Sen (270º + 79º) = - Cos 79º = -0,1908
Cos (d) = Cos (270º + A) = Sen A remplazamos
Cos 349º = Cos (270º + 79º) = Sen 79º= 0,9816
Tang (d) = tang (270º + A) = - Cotag A remplazamos
Tang 349º = tang (270º + 79º) = - Cotag 79º = -0,1943
Cotag (d) = Cotag (270º + A) = - Tang A remplazamos
Cotag 349º = Cotag (270º + 79º) = - Tang 79º = -5,1445
Segunda forma de resolverlo
El ángulo dado es d= 349º pero d = 360º - A
349º = 360º - A, entonces A = 360º - 349º = 11º
Sen (d) = Sen (360º - A) = - Sen A remplazamos
Sen 349º = Sen (360º - 11º) = - Sen 11º= -0,1908

10. Luis Gonzalo Revelo Pabón 54
Dpto. de Matemáticas - Goretti
Cos (d) = Cos (360º - A) = Cos A remplazamos
Cos 349º = Cos (360º -11º) = Cos 11º= 0,9816
Tang (d) = Tang (360º - A) = - Tang A remplazamos
Tang 349º = Tang (360º - 11º) = - Tang 11º= -0,1943
Cotag (d) = Cotag (360º - A) = - Cotag A. remplazamos
Cotag 349º = Cotag (360º - 11º) = - Cotag 11º= -5,1445.
TALLER
I.- Encontrar el valor de cada una de las siguientes expresiones:
1) Sen 30º + tan 45º
2) Cos 45º + Cos 60º
3) Sen 30º Cos 60º + Cos 30º Sen 60º
4) Cos 30º Cos 60º - Sen 30º Sen 60º
5)
6)
√ √
Respuestas: 1) 3/2 2) 3) 1 4) 0 5) 6) 1.
II.- Expresar en dos formas diferentes, cada una de las siguientes funciones trigonométricas:
1) Sen 130º 2) Cos 155º 3) tang 162º 4) Cotag 135 5) Sen 110º
6) Sen 200º 7) Cos 210º 8) tang 255º 9) Cotag 274º 10) Cos 181º
11) Cos 275 12) Sen 345º 13) Tang 284º 14) Cotag 305º 15)Sen 300º.
III.- Encontrar los valores exactos del seno, del coseno, y de la tangente de los siguientes ángulos.
a) 120º b) 210º c) 315º d) 215º e) 133º
IV.- Encontrar el valor de las siguientes funciones trigonométricas: a) Sen 125º14´ b) Cos 169º 40´ c) tang
200º 23´ d) Sen 341º 52´
REDUCCION DE UN ANGULO MAYOR A 360º AL PRIMER CUADRANTE.
Cuando un ángulo dado (d) es mayor a 360º grados, entonces para reducirlo al primer cuadrante se efec-
túa los siguientes pasos:
1.- Se divide al ángulo dado (d) entre 360º grados, entonces el ángulo dado (d) será igual a:
.d = 360ºn + r donde:
.d: ángulo dado mayor a 360º
.r: residuo.
.n: número de ciclos o vueltas. Siendo n un número entero positivo, negativo o cero
2.- Las razones trigonométricas: Seno, Coseno, tangente, cotangente, secante y cosecante del ángulo
dado (d) que es mayor a 360º son iguales a las mismas relaciones trigométricas del residuo (r). Es decir:
Sen (d) = Sen (360ºn + r) = Sen (r).
Cos (d) = Cos (360ºn + r) = Cos (r)
Tang (d) = tang (360ºn + r) = tang (r).
3.- Sí las razones trigonométricas: Seno, Coseno, Tangente, Cotangente, Secante y Cosecante del RE-
SIDUO (r), es menor a 90º grados, entonces la conversión habrá concluido, pero si el RESIDUO (r), es
mayor a 90º grados y menor a 360º grados, entonces debemos aplicar cualquiera de los métodos apli-
cados en los casos anteriores de Reducción de Ángulos al Primer Cuadrante.
Ejemplos:
Sen 400 = Sen (360º (1) +40º) = Sen 40º = 0,6427

11. Luis Gonzalo Revelo Pabón 55
Dpto. de Matemáticas - Goretti
Cos 850º = Cos (360º (2) + 130º) = Cos 130º = - Cos 50º = -.0,6427
Tang 1000º = tang(360º (2) +280º) =- tang 280º = - tang 80º = -5,6712
Sen 1949º = Sen (360º (5) + 149º) = Sen 149º = Sen 31º = 0,5150
REDUCCION PARA ANGULOS NEGATIVOS
DEFINICION 1: dos ángulos son opuestos si la suma de las magnitudes de sus ángulos es igual a cero
grados (0º).
DEFINICION 2: dos ángulos son opuestos si tienen igual magnitud, y sentidos contrarios.
Por ejemplo -3 y +3; -120º y 120º son ángulos opuestos.)
Cuando el ángulo dado (d) es negativo se sigue los siguientes pasos:
1.- Si el ángulo negativo es menor o igual a - 360º, entonces al ángulo negativo se lo convierte a un
ángulo positivo, para ello se emplea las siguientes ecuaciones, llamadas ecuaciones de los ANGULOS
OPUESTOS.
Ahora, por definición –d y +d son ángulos opuestos, entonces se cumple que:
Sen (-d) = Sen (360º - (+d))
Cos (-d) = Cos (360º - (+d))
Tang (-d) = Tang (360º - (+d))
2.- Sí el ángulo negativo es mayor a – 360º, entonces al ángulo negativo se lo convierte a un ángulo posi-
tivo, empleando como argumento la siguiente expresión: (360ºn – (+d)), en cada una de las relaciones
trigonométricas, con la condición de que . Así:
Sen (-d) = Sen (360ºn - (+d))
Cos (-d) = Cos (360ºn - (+d))
Tang (-d) = Tang (360ºn - (+d))
3.- Una vez convertido el ángulo negativo a un ángulo positivo, se aplican los criterios de reducción de
ángulos que se encuentran en el segundo, tercer y cuarto cuadrante como en los casos anteriores.

12. Luis Gonzalo Revelo Pabón 56
Dpto. de Matemáticas - Goretti
Ejemplos:
Sen (-100) = Sen (360º - (+100º)) = Sen (260º) = Sen (180º + 80º) = - Sen 80º = - 0,9848
Cos (- 200) = Cos (360º - (+200º)) = Cos (160º) = Cos (180º - 20º) = - Cos 20º = - 0,9396
Sen ( -300) = Sen (360º - (+300º)) = Sen (60º) = 0,8660
Tang ( - 290) = Tang( 360º - (+290º) = tang 70º = 2,7474
Cos (- 680º) = Cos (360ºn – (+680º)) n = 2 vueltas
Cos (- 680º) = Cos (360º( 2) – (+680º))
= Cos (720º - 680º)
= Cos 40º = 0,7660
Sen (- 2011) = Sen (360ºn – 2011) n = 6 vueltas
Sen (- 2011) = Sen (360º(6) – 2011)
= Sen (149º)
= Sen (180º -149º)
= Sen 31º = 0,5150
Tang (-1975) = tan (360ºn -1975º) n = 6 vueltas
= tan (360º(6) -1975º)
= tan (185º)
= tang (180º +5º)
= tag 5º
TALLER
1.- Encontrar el valor de las siguientes funciones trigonométricas:
a) Sen 455º
b) Cos 659º
c) tang 1234º
d) Sen 2361º
e) Cos 4231º
2.- Encontrar el valor de las siguientes funciones trigonométricas
a) Sen ( -23º)
b) Cos ( -234º)
c) tang ( – 354º)
d) Sen ( – 2356º)
e) Cos (– 1234º)
f) Tang ( – 379º)
g) Sen ( – 1256º)
h) Cos ( – 435º)