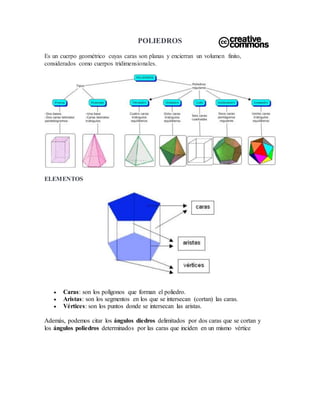
Poliedros
- 1. POLIEDROS Es un cuerpo geométrico cuyas caras son planas y encierran un volumen finito, considerados como cuerpos tridimensionales. ELEMENTOS Caras: son los polígonos que forman el poliedro. Aristas: son los segmentos en los que se intersecan (cortan) las caras. Vértices: son los puntos donde se intersecan las aristas. Además, podemos citar los ángulos diedros delimitados por dos caras que se cortan y los ángulos poliedros determinados por las caras que inciden en un mismo vértice
- 2. TEOREMAS El teorema de Euler para poliedros establece una relación entre los números de caras (C), aristas (A) y vértices (V) que se cumple para todo poliedro convexo. La relación es la siguiente: 1. C+V = A+2 2. 1/n = 1/A + 1/6 3. 1/r = 1/A + 1/6 4. n.C = 2A 5. r.V = 2A 6. 2A/r – A + 2A/n = 2 7. 1/n + 1/r = ½ + 1/A Donde: C = Número de caras V = Número de vértices A = Número de aristas n = Número de lados del polígono regular r = Número de aristas que convergen en los vértices EJEMPLO Supongamos que tenemos un prisma cuadrangular. Éste tiene seis caras, C=6, las dos bases y los cuatro paralelogramos de los laterales. También es conocido el número de vértices que tiene, V=8. ¿Cuántas aristas (A) tiene el prisma cuadrangular? C+V = A+2 A= C+V-2 A= 6+8-2 A=12
- 3. PRISMAS Un prisma es un poliedro que tienen dos caras paralelas e iguales llamadas bases y sus caras laterales son paralelogramos. ELEMENTOS Bases:Son las dos caras iguales y paralelas del prisma, una en la que se apoya y la otra su opuesta. Las bases son las que delimitan el prisma y sirven para poder calcular su altura. Caras laterales: Son las caras que comparten dos de sus lados con las bases. Un prisma tiene tantas caras laterales como lados tiene su base. La suma de sus áreas es la superficie lateral del prisma. Aristas: Son los lados de las bases y de las caras laterales. Vértices: Son los puntos en donde se encuentran cada par de aristas. Altura: Es la distancia entre las bases.
- 4. Diagonales: Son los segmentos que unen dos vértices no consecutivos del prisma. Se pueden trazar las diagonales de una cara o entre dos caras. TEOREMA Por el teorema de Euler, se puede saber el número de aristas (A) sabiendo el número de caras (C) y de vértices (V). A = C+V-2 Formulas Área= 2. Ab+Pb.h Volumen= Ab.h EJEMPLO Obtener el volumen del prisma rectangular
- 5. CILINDROS En geometría, un cilindro es una superficie de las denominadas cuádricas formada por el desplazamiento paralelo de una recta llamada generatriz a lo largo de una curva plana, denominada directriz del cilindro. ELEMENTOS Eje: lado AD, alrededor del cual gira el rectángulo.
- 6. Bases:son los círculos paralelos y congruentes que se generan al girar los lados AB y CD del rectángulo. Cada uno de estos lados es el radio de su círculo y también, el radio del cilindro. Altura: corresponde al mismo eje AD; es perpendicular a las bases y llega al centro de ellas. Esta es la razón por la que el cilindro es recto. Generatriz: es el lado BC, congruente con el lado AD, y que al girar forma la superficie lateral o manto del cilindro. TEOREMA Pitágoras EJEMPLO Un cilindro tiene por altura la misma longitud que la circunferencia de la base. Y la altura mide 125.66 cm. Calcular el área total y volumen: PIRAMIDE Una pirámide es un poliedro, que es un conjunto formado por un polígono (llamado base) y triángulos que tienen su base en cada lado poligonal; todos los triángulos tienen un vértice común llamado vértice de la pirámide. Los triángulos se llaman caras laterales. El lado común a dos caras laterales se llama arista, del mismo modo que cualquier lado de la base. El número total de las aristas es doble del número
- 7. de lados de la base. Estrictamente, el poliedro tiene vértices donde es el número de vértices de la base. ELEMENTOS Base: es el polígono cuyos puntos son los extremos de los segmentos que se unen con el punto exterior. Vértice de la pirámide: es el punto exterior al plano de la base. Arista lateral: es el segmento que une cada vértice del polígono con el vértice de la figura del espacio. Altura: es el segmento perpendicular del vértice de la pirámide al plano de la base. También lo es su medida. Cada lado de la base con el vértice de la pirámide al unirlos por sus extremos determina una región triangular, llamada cara lateral 1 Apotema: es un segmento perpendicular del vértice de la pirámide a un lado de la base. Área de la pirámide
- 8. El área de la pirámide se calcula mediante la suma del área de la base (Ab) y el área de los triángulos de las caras laterales (Al). A = Ab+Al Área de la pirámide regular La pirámide regular es aquella que tiene un polígono regular como base y es recta. Sea una pirámide regular con la base de N aristas. La fórmula del área de la pirámide regular es: A= N.L/2.(apb+ap) Volumen de la pirámide
- 9. El volumen de la pirámide es un tercio del área de la base de la pirámide (Ab) y su altura (h). V= 1/3. Ab.h EJEMPLO Calcula el área lateral, total y el volumen de una pirámide cuadrangular de 10 cm de arista básica y 12 cm de altura.
- 10. CONOS Un Cono se forma cuando una recta, generatriz, gira alrededor de otra, eje, con la que se corta en un punto. Es decir, cuando un triángulo rectángulo gira sobre uno de sus catetos (lados menores del triángulo) y determina un cuerpo geométrico, el cono. ELEMENTOS Base (B): es la cara plana inferior del cono, que en el caso del cono circular recto, es un círculo cuyo radio es uno de los catetos del triángulo generador. Altura (h): distancia del plano de la base al vértice de la pirámide. Vértice (V): punto donde confluyen las infinitas generatrices. Generatriz (g): Línea que al girar sobre el eje del cono engendra la superficie cónica de revolución. Superficie generatriz (Sg):en el cono recto de revolución, es el triángulo rectángulo que lo engendra al girar 360° sobre uno de sus catetos, que es el eje de rotación y, que es a su vez, la altura del cono. El otro cateto es el radio de la base. La hipotenusa la generatriz (g). Por el teorema de Pitágoras la generatriz del cono será igual a: Área lateral de un cono
- 11. Área de un cono Volumen de un cono EJEMPLO Calcula el área lateral de un cono cuya generatriz mide 6 cm y el radio de la base es de 2 cm. En este ejercicio solo nos piden que busquemos el área lateral. Buscamos la formula y sustituimos en ella por los valores de la generatriz, el radio y el Pi= π, que es siempre (3.14) Área lateral= π.r.g Al= (3.14) (12cm²) Al= 37.68 cm²
- 12. ESFERAS Una superficie esférica es la superficie engendrada por una circunferencia que gira sobre su diámetro. Una esfera es la región del espacio que se encuentra en el interior de una superficie esférica. ELEMENTOS Centro: Punto interior que equidista de cualquier punto de la superficie de la esfera, es el centro del círculo. Radio: Distancia del centro a un punto de la superficie de la esfera. Cuerda: Segmento que une dos puntos de la superficie esférica. Diámetro: Cuerda que pasa por el centro. Polos: Son los puntos del eje de giro que quedan sobre la superficie esférica. Si consideramos una semicircunferencia que gira sobre su diámetro, la superficie curva que se genera es la superficie esférica. Área El área de la esfera es igual a 4 multiplicado por π(pi), y el resultado se multiplica por el cuadrado del radio de la esfera A= 4 • π • r 2 Volumen
- 13. El volumen de la esfera es igual a 4 multiplicado por π (pi), el resultado se multiplica por el cubo del radio de la esfera y lo que resulta se divide entre 3 V = 4 • π • r 3/ 3 EJEMPLO Calcular el área y el volumen de una esfera inscrita en un cilindro de 2 m de altura.