El documento presenta tres oraciones sobre álgebra lineal: 1) Explica cómo calcular la pendiente de una recta y provee ejemplos. 2) Introduce el concepto de sistemas de ecuaciones lineales con dos incógnitas. 3) Describe propiedades fundamentales como la suma y multiplicación de ecuaciones que permiten resolver dichos sistemas.

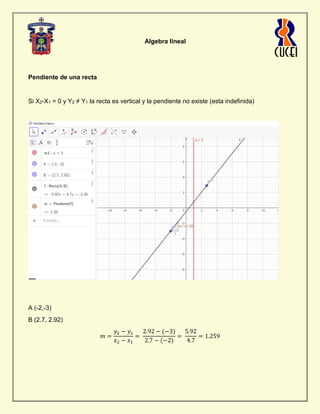
1. Algebra lineal
Pendiente de una recta
Si X2-X1 = 0 y Y2 ≠ Y1 la recta es vertical y la pendiente no existe (esta indefinida)
A (-2,-3)
B (2.7, 2.92)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1
=
2.92 − (−3)
2.7 − (−2)
=
5.92
4.7
= 1.259

2. A (-3,-3.3)
B (1.7, 2.62)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1
=
2.62 − (−3.3)
1.7 − (−3)
=
5.92
4.7
= 1.259

3. A (2.12,-4.2)
B (5.16, 1.56)
𝑚 =
𝑦2 − 𝑦1
𝑥2 − 𝑥1
=
1.56 − (−4.2)
5.16 − 2.12
=
5.76
3.04
= 1.89

4. Dos ecuaciones lineales con dos incógnitas
Considere el siguiente sistema de dos ecuaciones lineales con dos incógnitas x y y
𝑎11𝑥 + 𝑎12𝑦 = 𝑏1
𝑎21𝑥 + 𝑎22𝑦 = 𝑏2
Donde a12, a21, a22, b1 y b2 son números dados. Cada una de estas ecuaciones corresponde a
una línea recta. Cualquier par de números reales (x, y) que satisface el sistema (1.1.1) se
denomina solución. Las preguntas que surgen en forma natural son ¿Tiene este sistema varias
soluciones y, de ser así, cuantas? Se responderán estas preguntas después de ver algunos
ejemplos, en los cuales se usaran propiedades del algebra elemental.
La propiedad A establece que si se suman dos ecuaciones se obtiene una tercera ecuación
correcta.
La propiedad B establece que si se multiplican ambos lados de una ecuación por una constante
se obtiene una segunda ecuación valida. Los casos más interesantes de la propiedad B se
presentan cuando c diferente de 0, ya que aunque la ecuación 0-0 es correcta, no es muy útil.
Ejemplo 1.1.1 Sistema con una solución única
Considere el sistema
3𝑥 − 2𝑦 = 4
5𝑥 + 2𝑦 = 12
8𝑥 = 16
𝑥 = 2
Si se suman las dos ecuaciones se tiene por la propiedad A, la siguiente ecuación 8x = 16 (es
decir x = 2). Entonces, si se despeja de la segunda ecuación, 2y = 12 – 5x = 12 – 10 = 2,
entonces y = 1. Así, el par (2, 1) satisface el sistema (1.1.2) y la forma en que se encontró la
solución muestra que es el único par de números que lo hace. Es decir, el sistema (1.1.2)
tiene una solución única.
𝑥 = 2
5𝑥 + 2𝑦 = 12
2𝑦 = 12 − 5𝑥 = 12 − 5(2) = 12 − 10
2𝑦 = 2
𝑦 =
2
2
= 1
𝑦 = 1

5.  Instrucciones:
1. Lee cuidadosamente lo que se te pide en cada reactivo
2. Es importante que cada uno de los reactivos cuente con el proceso de solución.
Considere el siguiente sistema de dos ecuaciones lineales con dos incógnitas x y y:
𝑎11 𝑥 + 𝑎12 𝑦 = 𝑏1
𝑎21 𝑥 + 𝑎 22 𝑦 = 𝑏2
Donde a11, a12, a21, a22, b1 y b2 son números dados. Cada una de estas ecuaciones
corresponde a una línea recta. Cualquier par de números reales (x, y) que satisface el sistema.
 Sistema con una solución única
 Sistema con un número infinito de soluciones
 Sistema sin solución

6. 1. 𝑥 + 𝑦 = 3
𝑥 + 2𝑦 = −8
2. 2𝑥 − 3𝑦 = 3
−2𝑥 + 3𝑦 = −3
0 = 0
𝑥 + 𝑦 − 𝑦 = 3 − 𝑦 𝑥 = 3 − 𝑦
3 − 𝑦 + 2𝑦 = −8 𝑦 = −8 − 3 𝑦 = −11
𝑥 = 3 − (−11) = 14 𝑥 = 14
2𝑥 − 3𝑦 = 3 𝑥 =
3+3𝑦
2
−2𝑥 + 3𝑦 = −3 −2 (
3+3𝑦
2
) + 3𝑦 = −3
−2 (
3+3𝑦
2
) · 2 + 3𝑦(2) = −3(2)
−2(3 + 3𝑦) + 6𝑦 = −6 −6 − 6𝑦 + 6𝑦 = −6
− 6 = −6

7. 3. 4𝑥 + 5𝑦 = 0
−2𝑥 − 𝑦 = 3
4. −2𝑥 = 1
4𝑥 − 3𝑦 = 0
4𝑥 + 5𝑦 = 0 𝑥 = −
5𝑦
4
−2 (−
5𝑦
4
) − 𝑦 = 3 −2 (−
5𝑦
4
) · 4 − 𝑦(4) = 3(4)
−2(−5𝑦) − 4𝑦 = 12 10𝑦 − 4𝑦 = 12
6𝑦 = 12 𝑦 =
12
6
𝑦 = 2
𝑥 = −
5(2)
4
= −
10
4
= −
5
2
𝑥 = −
5
2
−2𝑥 = 1 𝑥 = −
1
2
4 (−
1
2
) − 3𝑦 = 0 4 (−
1
2
) · 2 − 3𝑦(2) = 0(2)
4(−1) − 6𝑦 = 0 − 4 − 6𝑦 = 0 − 6𝑦 = 4
𝑦 =
4
−6
𝑦 = −
2
3

8. 5. 7𝑥 + 3𝑦 = 0
−5𝑥 + 10𝑦 = 0
7𝑥 + 3𝑦 = 0 𝑥 = −
3𝑦
7
− 5 (−
3𝑦
7
) + 10𝑦 = 0 5 (
3𝑦
7
) + 10𝑦 = 0
15𝑦
7
+ 10𝑦 = 0
15𝑦
7
+
10𝑦(7)
7
= 0
15𝑦 + (10𝑦 · 7)
7
= 0
15𝑦 + 70𝑦
7
= 0
85𝑦
7
= 0
85𝑦 · 7
7
= 0(7)
85𝑦 = 0 𝑦 =
0
85
𝑦 = 0
𝑥 = −
3(0)
7
=
0
7
= 0 𝑥 = 0

9. 6. 3𝑥 − 7𝑦 = −5
4𝑥 − 3𝑦 = −2
3𝑥 − 7𝑦 = −5 𝑥 =
−5+7𝑦
3
4 (
−5+7𝑦
3
) · 3 − 3𝑦(3) = −2(3)
4(−5 + 7𝑦) + 9𝑦 = −6 − 20 + 28𝑦 + 9𝑦 = −6
19𝑦 = −6 + 20 𝑦 =
14
19
𝑥 =
−5 + 7(
14
19
)
3
𝑥 =
−5 +
98
19
3
𝑥 =
−
5(19)
19
+
98
19
3
𝑥 = −
−5(19) + 98
19
3
=
−95 + 98
19
3
=
−5(19) + 98
19
3
=
3
19
3
𝑥 =
3
19 · 3
=
3
57
𝑥 =
1
19

10. 7. 7𝑥 + 4𝑦 = 1
−7𝑥 − 4𝑦 = −3
7𝑥 + 4𝑦 = 1 𝑥 =
1−4𝑦
7
−7 (
1−4𝑦
7
) − 4𝑦 = −3 −
7(1−4𝑦)
7
− 4𝑦 = −3
−(1) − (−4𝑦) − 4𝑦 = −3
−1 + 4𝑦 + 4𝑦 = −3 −1 = −3 Falso ∴ el sistema no tiene solución
𝑆𝐼𝑁 𝑆𝑂𝐿𝑈𝐶𝐼Ó𝑁

11. 8. 7𝑥 + 4𝑦 = 0
−7𝑥 − 4𝑦 = 0
7𝑥 + 4𝑦 = 0 𝑥 = −
4𝑦
7
− 7 (−
4𝑦
7
) − 4𝑦 = 0 7 (
4𝑦
7
) − 4𝑦 = 0
4𝑦 − 4𝑦 = 0 0 = 0

12. 9. −13𝑥 + 3𝑦 = 7
5𝑥 + 22𝑦 = 9
5𝑥 + 22𝑦 = 16 𝑥 =
16−22𝑦
5
− 13 (
16−22𝑦
5
) · 5 + 3𝑦(5) = 7 · 5 −13(16 − 22𝑦 ) + 15𝑦 = 35
−208 + 286𝑦 + 15𝑦 = 35 301𝑦 = 35 + 208 301𝑦 = 243
𝑦 =
243
301
𝑥 =
16 − 22(
243
301
)
5
𝑥 =
16 −
5346
301
5
𝑥 =
−
4816 − 5346
301
5
𝑥 =
−
530
301
5
𝑥 = −
530
1505
𝑥 = −
106
301

13. 10.9𝑥 − 3𝑦 = −3
−2𝑥 + 4𝑦 = 1
9𝑥 − 3𝑦 = −3 𝑥 =
−3+3𝑦
9
=
3(−1+𝑦)
3·3
=
−1+𝑦
3
− 2 (
−1+𝑦
3
) + 4𝑦 = 1 − (
2(−1+𝑦)
3
) +
4𝑦(3)
3
= 1
2 − 2𝑦 + 12𝑦
3
= 1
2 + 10𝑦
3
= 1
(3)2 + 10𝑦
3
= 1(3)
10𝑦 = 3 − 2 10𝑦 = 1 𝑦 =
1
10
𝑥 =
−1 +
1
10
3
𝑥 =
−1 · 10
10
+
1
10
3
𝑥 =
−1 · 10 + 1
10
3
𝑥 =
−10 + 1
10
3
𝑥 =
−9
10
3
𝑥 =
−
9
10
3
𝑥 = −
3
10

14. 11.−2𝑥 + 3𝑦 = 3
2𝑥 − 3𝑦 = −3
−2𝑥 + 3𝑦 = 3 𝑥 = −
3+3𝑦
2
2𝑥 − 3𝑦 = −3 2 (−
3+3𝑦
2
) − 3𝑦 = −3
−
2(3 + 3𝑦)
2
− 3𝑦 = −3 − 3 + 3𝑦 − 3𝑦 = −3
− 3 = −3

15. 12. 𝑥 + 2𝑦 = 5
3𝑥 + 4𝑦 = 6
𝑥 + 2𝑦 = 5 𝑥 = 5 − 2𝑦
3𝑥 + 4𝑦 = 6 3(5 − 2𝑦) + 4𝑦 = 6 15 − 6𝑦 + 4𝑦 =
6
−6𝑦 + 4𝑦 = 6 − 15 − 2𝑦 = −9 𝑦 =
−9
−2
𝑦 =
9
2
𝑥 = 5 − 2 (
9
2
) 𝑥 = 5 −
2 · 9
1 · 2
𝑥 = 5 −
18
2
𝑥 = 5 −
9
1
𝑥 = 5 − 9 𝑥 = −4

16. 13. 𝑦 = 3
−2𝑥 + 4𝑦 = 8
𝑦 = 3
−2𝑥 + 4𝑦 = 8 −2𝑥 + 4(3) = 6 − 2𝑥 + 12 = 6
−2𝑥 = 6 − 12 − 2𝑥 = −4 𝑥 =
−4
−2
𝑥 =
2
1
𝑥 = 2

17. 14.7𝑥 + 2𝑦 = −9
2𝑦 = −6
2𝑦 = −6 𝑦 =
−6
2
𝑦 = −
6
2
𝑦 = −3
7𝑥 + 2𝑦 = −9 7𝑥 + 2(−3) = −9 7𝑥 − 6 = −9
7𝑥 = −9 + 6 7𝑥 = −3 𝑥 =
−3
7
𝑥 = −
3
7