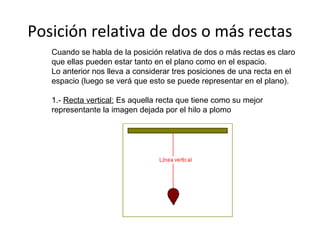
1. Posición relativa de dos o más rectas
Cuando se habla de la posición relativa de dos o más rectas es claro
que ellas pueden estar tanto en el plano como en el espacio.
Lo anterior nos lleva a considerar tres posiciones de una recta en el
espacio (luego se verá que esto se puede representar en el plano).
1.- Recta vertical: Es aquella recta que tiene como su mejor
representante la imagen dejada por el hilo a plomo

2. Posición relativa de dos o más rectas
2.- Recta horizontal: es aquella recta que tiene como su mejor
representante la imagen que deja la superficie de las aguas en
reposo, lo que en algunos textos este concepto está referido a la línea
que se observa en el horizonte.
NOTA: cuando el hilo a plomo se encuentra con las aguas en reposo se dice
que, el hilo a plomo ha caído PERPENDICULARMENTE sobre la
superficie de las aguas en reposo.

3. Posición relativa de dos o más rectas
3.- Línea oblicua : Es aquella línea recta que no es
vertical ni tampoco es horizontal, y su representación
está dada por:

4. Posición relativa de dos o más rectas
Dos o más rectas en el
plano pueden tener las
siguientes posiciones
Ser paralelas
No ser paralelas
se dice que dos o más
rectas son paralelas si ellas
no tienen ningún punto en
común, esto se muestra:
L
L’
L’’
Y se dice que la recta L es paralela a L’ y que la
recta L’ es paralela a L’’ y que la recta L
también es paralela a L’’. Esta afirmación se
denota por:

5. Posición relativa de dos o más rectas
No ser paralelas
Cuando ellas tienen
sólo un punto en
común
Su representación puede tomar dos formas:
L L’ L
L’
En este caso se
dice que las rectas
no son
perpendiculares En este caso se dice
que ellas son rectas
perpendiculares, lo que
se denota:

6. Rectas cortadas por una transversal o por una
secante
Se dice que una línea recta es una secante o una transversal
si ella intersecta a una figura geométrica cualquiera
Ya se dijo que dos rectas cualesquiera en el plano pueden ser o no
ser paralelas. Si ellas no son paralelas se intersectan en un punto,
cuya intersección siempre se denota por una letra mayúscula, en este
caso tomaremos la letra P, tal como se muestra en la figura:
L
L’
P

7. Rectas cortadas por una transversal o por
una secante
Es claro que una sola recta divide al plano en dos semiplanos, es
decir el plano queda dividido en tres subconjuntos, a saber, los dos
semiplanos y la recta propiamente tal, de tal manera que la
intersección dos a dos es vacía y la unión de ellos tres es el plano, ver
figura:
Recta L
SEMIPLANO 2
SEMIPLANO 1

8. Rectas cortadas por una transversal o
por una secante
Cuando dos rectas L y L’ se intersectan en un punto se dice que
ellas dividen al plano en cuatro subconjuntos, llamados cuadrantes
(aunque este nombre es usado frecuentemente cuando las rectas
son perpendiculares), de tal forma que los cinco subconjunto que
así aparecen, la intersección dos a dos es vacía y la unión es el
plano.
L
L’
P Cuadrante 1
Cuadrante 2
Cuadrante 3
Cuadrante 4

9. Rectas cortadas por una transversal o por
una secante
Aunque no sabemos la definición de ángulo, utilizaremos la
noción intuitiva que podríamos tener, es así que al observar las
dos rectas que se intersectan en un punto nos encontramos
con que ellas generan aparentemente cuatro ángulos,
llamados ángulos opuestos por el vértice
P
L
L’
1
2
3
4
Los ángulos 1 y 3 , 2 y 4 se llaman ángulos opuestos por el
vértice. Este nombre nace del hecho de que los lados de los
ángulo 1 y 3 , 2 y 4 son rayos que están sobre L y L’

10. Rectas cortadas por una transversal o por
una secante
Consideremos dos rectas L y L’ cortadas por una secante L’’, tal como
Lo muestra la figura:
L
L’
L’’
1 2
34
5 6
78
En este caso se han formado cuatro pares
de ángulos opuestos por el vértice, a saber:
1 y 3 ; 2 y 4 ; 5 y 7 ; 6 y 8

11. Rectas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Estos ocho ángulos que determinan estas tres rectas, existen grupos
de ellos que reciben un nombre especial:
Ángulos internos, externos, alternos internos, alternos externos y
ángulos correspondientes.

12. Rectas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Ángulos internos: son aquellos ángulos comprendidos entre las
rectas L y L’, ellos son: 3 , 4 , 5 y 6
Ángulos externos: son aquellos que están fuera de las rectas
L y L’’ , ellos son : 1 , 2 , 7 y 8

13. Rectas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Ángulos alternos internos: son aquellos ángulos que están entre
las rectas L y L’ pero a distintos lados de la recta L’’, ellos son los
ángulos 3 y 5 , y también los ángulos 4 y 6.
Ángulos alternos externos: son aquellos ángulos que están fuera de las
rectas L y L’ pero a distintos lados de la recta L’’, ellos son los ángulos 1 y
7, y también los ángulos 2 y 8.

14. Rectas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Ángulos correspondientes: son dos ángulos tales que están al mismo
lado de la secante L’’ , uno es interno, el otro externo, pero no
adyacentes. Estos pares de ángulos son: 1 y 5 ; 4 y 8 ; 2 y 6 ; 3 y 7

15. Rectas paralelas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Las rectas L y L’ son paralelas y L’’ es una secante cualquiera,
entonces, los siguientes pares de ángulos son congruentes, es decir
tienen la misma medida:
3 y 5 ; 4 y 6 son ángulos alternos internos
2 y 8 ; 1 y 7 son ángulos alternos externos
4 y 8 ; 2 y 6 son ángulos correspondientes
1 y 5 ; 3 y 7 son ángulos correspondientes

16. Rectas paralelas cortadas por una transversal
o por una secante
L
L’
L’’
1 2
34
5 6
78
Uno de los conceptos que más ha dado problemas en el campo de la
Geometría es justamente el de rectas paralelas.
Esto ha sido posible simplificarlo al usar el concepto de congruencia y
medida del ángulo, es así que dos rectas pueden definirse como
rectas paralelas, de la siguiente manera:

17. Rectas paralelas cortadas por una transversal o
por una secante
L
L’
L’’
1 2
34
5 6
78
Se dice que dos rectas L y L’ son paralelas cuando y
sólo cuando los ángulos correspondiente 3 y 7 son
congruentes, como así también los ángulos 2 y 6 son
congruentes

18. Rectas paralelas cortadas por una transversal
o por una secante
L
L’
L’’
1 2
34
5 6
78
También se dice que dos rectas son paralelas cuando y
sólo cuando los ángulos 3 y 6 son suplementarios
Lo mismo si se consideran los pares de ángulos: 4 y 5 ; 1 y 8 ; 2 y 7.