1. RESUMO DE FÓRMULAS PARA GEOMETRÍA ANALÍTICA B: 1ª ÁREA
Prof. Elismar R. Oliveira
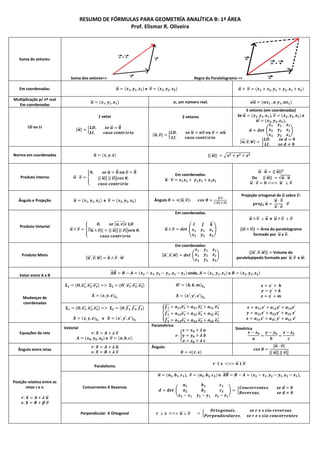
Soma de vetores:
Soma dos vetores=> Regra do Paralelogramo =>
Em coordenadas: 𝒖 = (𝒙 𝟏 , 𝒚 𝟏 , 𝒛 𝟏 ) e 𝒗 = (𝒙 𝟐 , 𝒚 𝟐 , 𝒛 𝟐 ) 𝒖 + 𝒗 = (𝒙 𝟏 + 𝒙 𝟐 , 𝒚 𝟏 + 𝒚 𝟐 , 𝒛 𝟏 + 𝒛 𝟐 )
Multiplicação p/ nº real
𝒖 = (𝒙 𝟏 , 𝒚 𝟏 , 𝒛 𝟏 ) 𝜶, um número real. 𝜶𝒖 = (𝜶𝒙 𝟏 , 𝜶 𝒚 𝟏 , 𝜶𝒛 𝟏 )
Em coordenadas
3 vetores (em coordenadas)
1 vetor 2 vetores Se 𝒖 = (𝒙 𝟏 , 𝒚 𝟏 , 𝒛 𝟏 ), 𝒗 = (𝒙 𝟐 , 𝒚 𝟐 , 𝒛 𝟐 ) e
𝒘 = (𝒙 𝟑 , 𝒚 𝟑 , 𝒛 𝟑 ),
𝒙𝟏 𝒚𝟏 𝒛𝟏
LD ou LI
{𝒖} = 𝑳𝑫, 𝒔𝒆 𝒖 = 𝟎
𝒅 = 𝒅𝒆𝒕 𝒙 𝟐 𝒚 𝟐 𝒛 𝟐
𝑳𝑰, 𝒄𝒂𝒔𝒐 𝒄𝒐𝒏𝒕𝒓á𝒓𝒊𝒐 𝑳𝑫, 𝒔𝒆 𝒖 = 𝜶𝒗 𝒐𝒖 𝒗 = 𝜶𝒖 𝒙𝟑 𝒚𝟑 𝒛𝟑
{𝒖, 𝒗} =
𝑳𝑰, 𝒄𝒂𝒔𝒐 𝒄𝒐𝒏𝒕𝒓á𝒓𝒊𝒐 𝑳𝑫, 𝒔𝒆 𝒅 = 𝟎
{𝒖, 𝒗, 𝒘} =
𝑳𝑰, 𝒔𝒆 𝒅 ≠ 𝟎
Norma em coordenadas 𝒖 = (𝒙, 𝒚, 𝒛) | 𝒖| = 𝒙𝟐+ 𝒚𝟐+ 𝒛𝟐
𝟎, 𝒔𝒆 𝒖 = 𝟎 𝒐𝒖 𝒗 = 𝟎 𝒖⋅ 𝒖=| 𝒖 𝟐
Em coordenadas:
Produto interno 𝒖⋅ 𝒗= | 𝒖 | 𝒗 𝒄𝒐𝒔 𝜽, Ou | 𝒖 | = 𝒖 ⋅ 𝒖
𝒖⋅ 𝒗 = 𝒙𝟏 𝒙𝟐+ 𝒚𝟏 𝒚𝟐+ 𝒛𝟏 𝒛𝟐
𝒄𝒂𝒔𝒐 𝒄𝒐𝒏𝒕𝒓á𝒓𝒊𝒐 𝒖 ⋅ 𝒗 = 𝟎 <=> 𝒖 ⊥ 𝒗
Projeção ortogonal de 𝒖 sobre 𝒗:
𝒖⋅𝒗
Ângulo e Projeção 𝒖 = 𝒙 𝟏 , 𝒚 𝟏 , 𝒛 𝟏 e 𝒗 = (𝒙 𝟐 , 𝒚 𝟐 , 𝒛 𝟐 ) Ângulo 𝜽 = ∢(𝒖, 𝒗): 𝒄𝒐𝒔 𝜽 = 𝒖⋅ 𝒗
| 𝒖 | 𝒗 𝒑𝒓𝒐𝒋 𝒗 𝒖 = 𝒗
𝒗⋅ 𝒗
Em coordenadas:
𝒖∧ 𝒗 ⊥ 𝒖 e 𝒖∧ 𝒗 ⊥ 𝒗
𝟎, 𝒔𝒆 {𝒖, 𝒗}é 𝑳𝑫 𝒊 𝒋 𝒌
Produto Vetorial
𝒖 ∧ 𝒗 = || 𝒖 ∧ 𝒗|| = | 𝒖 | 𝒗 𝒔𝒆𝒏 𝜽, 𝒖 ∧ 𝒗 = 𝒅𝒆𝒕 𝒙𝟏 𝒚𝟏 𝒛𝟏 ||𝒖 ∧ 𝒗|| = Área do paralelogramo
𝒄𝒂𝒔𝒐 𝒄𝒐𝒏𝒕𝒓á𝒓𝒊𝒐 𝒙𝟐 𝒚𝟐 𝒛𝟐 formado por 𝒖 e 𝒗.
Em coordenadas:
𝒙𝟏 𝒚𝟏 𝒛𝟏
| 𝒖 , 𝒗, 𝒘 | = Volume do
Produto Misto 𝒖 , 𝒗, 𝒘 = 𝒅𝒆𝒕 𝒙 𝟐 𝒚 𝟐 𝒛𝟐
𝒖 , 𝒗, 𝒘 = 𝒖 ∧ 𝒗 ⋅ 𝒘 𝒙𝟑 𝒚𝟑 𝒛𝟑 paralelepípedo formado por 𝒖, 𝒗 e 𝒘.
𝑨𝑩 = 𝑩 − 𝑨 = 𝒙 𝟐 − 𝒙 𝟏 , 𝒚 𝟐 − 𝒚 𝟏 , 𝒛 𝟐 − 𝒛 𝟏 onde, 𝑨 = 𝒙 𝟏 , 𝒚 𝟏 , 𝒛 𝟏 e 𝑩 = 𝒙 𝟐 , 𝒚 𝟐 , 𝒛 𝟐
Vetor entre A e B
𝚺 𝟏 = {𝑶, 𝒆 𝟏 , 𝒆 𝟐 , 𝒆 𝟑 } => 𝚺 𝟐 = {𝑶′, 𝒆 𝟏 , 𝒆 𝟐 , 𝒆 𝟑 } 𝑶′ = 𝒉, 𝒌, 𝒎 𝚺𝟏 𝒙 = 𝒙′ + 𝒉
𝒚 = 𝒚′ + 𝒌
Mudanças de 𝑿 = 𝒙, 𝒚, 𝒛 𝚺𝟏 𝑿 = 𝒙′, 𝒚′, 𝒛′ 𝚺𝟐 𝒛 = 𝒛′ + 𝒎
coordenadas
𝚺 𝟏 = {𝑶, 𝒆 𝟏 , 𝒆 𝟐 , 𝒆 𝟑 } => 𝚺 𝟐 = {𝑶, 𝒇 𝟏 , 𝒇 𝟐 , 𝒇 𝟑 } 𝒇 𝟏 = 𝒂 𝟏𝟏 𝒆 𝟏 + 𝒂 𝟐𝟏 𝒆 𝟐 + 𝒂 𝟑𝟏 𝒆 𝟑 𝒙 = 𝒂 𝟏𝟏 𝒙′ + 𝒂 𝟏𝟐 𝒚′ + 𝒂 𝟏𝟑 𝒛′
𝒇 𝟐 = 𝒂 𝟏𝟐 𝒆 𝟏 + 𝒂 𝟐𝟐 𝒆 𝟐 + 𝒂 𝟑𝟐 𝒆 𝟑 𝒚 = 𝒂 𝟐𝟏 𝒙′ + 𝒂 𝟐𝟐 𝒚′ + 𝒂 𝟐𝟑 𝒛′
𝑿 = 𝒙, 𝒚, 𝒛 𝚺𝟏 e 𝑿 = 𝒙′, 𝒚′, 𝒛′ 𝚺𝟐 𝒇 𝟑 = 𝒂 𝟏𝟑 𝒆 𝟏 + 𝒂 𝟐𝟑 𝒆 𝟐 + 𝒂 𝟑𝟑 𝒆 𝟑 𝒛 = 𝒂 𝟑𝟏 𝒙′ + 𝒂 𝟑𝟐 𝒚′ + 𝒂 𝟑𝟑 𝒛′
Paramétrica
Vetorial Simétrica
𝒙 = 𝒙𝟎+ 𝝀 𝒂
Equações da reta 𝒓: 𝑿 = 𝑨 + 𝝀 𝒗 𝒙− 𝒙𝟎 𝒚− 𝒚𝟎 𝒛− 𝒛𝟎
𝒓: 𝒚 = 𝒚 𝟎 + 𝝀 𝒃 = =
𝑨 = (𝒙 𝟎 , 𝒚 𝟎 , 𝒛 𝟎 ) e 𝒗 = 𝒂, 𝒃, 𝒄 . 𝒂 𝒃 𝒄
𝒛 = 𝒛𝟎+ 𝝀 𝒄
𝒓: 𝑿 = 𝑨 + 𝝀 𝒖 Ângulo: |𝒖 ⋅ 𝒗|
Ângulo entre retas 𝒄𝒐𝒔 𝜽 =
𝒔: 𝑿 = 𝑩 + 𝝀 𝒗 𝜽 = ∢(𝒓, 𝒔) | 𝒖 | 𝒗
𝒓 ∥ 𝒔 <=> 𝒖 ∥ 𝒗
Paralelismo
𝒖 = (𝒂 𝟏 , 𝒃 𝟏 , 𝒄 𝟏 ), 𝒗 = (𝒂 𝟐 , 𝒃 𝟐 , 𝒄 𝟐 ) e 𝑨𝑩 = 𝑩 − 𝑨 = 𝒙 𝟐 − 𝒙 𝟏 , 𝒚 𝟐 − 𝒚 𝟏 , 𝒛 𝟐 − 𝒛 𝟏 ,
Posição relativa entre as
𝒂𝟏 𝒃𝟏 𝒄𝟏
retas r e s: Concorrentes X Reversas 𝑪𝒐𝒏𝒄𝒐𝒓𝒓𝒆𝒏𝒕𝒆𝒔, 𝒔𝒆 𝒅 = 𝟎
𝒅 = 𝒅𝒆𝒕 𝒂𝟐 𝒃𝟐 𝒄𝟐 =
𝑹𝒆𝒗𝒆𝒓𝒔𝒂𝒔, 𝒔𝒆 𝒅 ≠ 𝟎
𝒙𝟐− 𝒙𝟏 𝒚𝟐− 𝒚𝟏 𝒛𝟐− 𝒛𝟏
𝒓: 𝑿 = 𝑨 + 𝝀 𝒖
𝒔: 𝑿 = 𝑩 + 𝜷 𝒗
𝑶𝒓𝒕𝒐𝒈𝒐𝒏𝒂𝒊𝒔, 𝒔𝒆 𝒓 𝒆 𝒔 𝒔ã𝒐 𝒓𝒆𝒗𝒆𝒓𝒔𝒂𝒔
Perpendicular X Ortogonal 𝒓 ⊥ 𝒔 <=> 𝒖 ⊥ 𝒗 =
𝑷𝒆𝒓𝒑𝒆𝒏𝒅𝒊𝒄𝒖𝒍𝒂𝒓𝒆𝒔, 𝒔𝒆 𝒓 𝒆 𝒔 𝒔ã𝒐 𝒄𝒐𝒏𝒄𝒐𝒓𝒓𝒆𝒏𝒕𝒆𝒔