1. El documento habla sobre curvas planas y funciones vectoriales. Define conceptos como curva suave, cerrada, simple y cómo queda parametrizada una curva plana en el espacio. También explica qué es una función vectorial y su relación con curvas espaciales. 2. Describe cómo calcular la velocidad, aceleración y vector tangente de una función vectorial, así como las reglas para derivar diferentes funciones vectoriales. 3. Explica cómo encontrar la velocidad, rapidez y aceleración de una partícula que se desplaza

1. 1. Curvas planas:
1.1. Defina curva plana
MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
Si f y g son funciones continuas de t en un intervalo I, entonces a las ecuaciones
se les llama ecuaciones parametricas; y
puntos (x, y) que se obtiene cuando t varia sobre el intervalo I, se le llama la grafica de las
ecuaciones parametricas. A las ecuaciones parametricas y a la grafica, juntas, es lo que se llama
una curva plana, que se denota con C.
1.2. ¿Qué significa que una curva sea suave?
Una curva C representada por
son continuas en I y no son simultáneamente 0, excepto posiblemente en los puntos terminales
la curva C se dice que es suave a trozos si es suave en todo sub
1.3. ¿Cuándo una curva es cerrada? ¿Cuándo una curva es simple?
Una curva C dada por r(t) para
las integrales de línea, se puede concluir que si
entonces la integral de línea sobre toda curva cerrada es 0.
Una curva C dada por
es decir

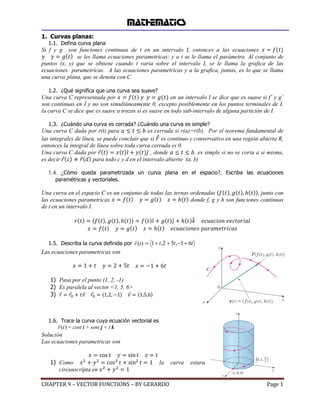
2. para todo c y d en el intervalo abierto (a, b)
1.4. ¿Cómo queda parametrizada un curva plana en el espacio?.
paramétricas y vectoriales.
Una curva en el espacio C es un conjunto de todas las ternas ordenadas
las ecuaciones parametricas
de t en un intervalo I.
1.5. Describa la curva definida por
Las ecuaciones parametricas son
1) Pasa por el punto (1, 2, -1)
2) Es paralela al vector 1, 5, 6
3)
1.6. Trace la curva cuya ecuación vectorial es
r (t) = cost i + sent j + t k
Solución
Las ecuaciones parametricas son
1) Como
circunscripta en
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
a t se le llama el parámetro. Al conjunto de
enota en un intervalo I se dice que es suave si f’ y g’
de I.
a sub-intervalo de alguna partición de I.
es cerrada si r(a)=r(b). Por el teorema fundamental de
!
es continuo y conservativo en una región abierta R,
# $# , donde , es simple si no se corta a si
Escriba
misma,
las ecuaciones
, junto con
% donde f, g y h son funciones continuas
# $# '(

3. )

4. *+,(

5. +
*-
% (

6. )

7. *+,(./
0(
*

8. .
r (t) = 1+ t,2 + 5t,−1+ 6t
% 1
1
23 %
23 la curva estara
Page 1
(

9. +
*-

10. MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
2) Como z=t (positivo) la curva se mueve hacia arriba
3) El movimiento es anti-horario a partir del plano XY
4) La curva es llama hélix (helicoide)
1.7. Utilice una computadora para trazar las siguientes curvas:
)
θ θ
a x sen y
= − =
= =
θ
) 2cos3
b x y
) 2cot
θ
c x y
= =
3
)
θ
d x y
( 1
)
2
3
+
=
θ
e x t y t z
)
=
= = =
CHAPTER 9 – VECTOR FUNCTIONS
1 cos ( )
cicloide
3
−
3 ( )
sen θ
hipocicloide
2
2 ( )
sen brujadeAgnesi
3
θ
θ
( )
t t cúbicaalabeada
– BY GERARDO
foliodeDescartes
2 2
1
3
3
2
− ≤ ≤
+
θ
θ
Page 2

11. 2. Funciones vectoriales
MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
2.1. ¿Qué es una función vectorial?
Definición:
Una función de la forma
vectorial?. Dé ejemplos.
# $# (,(-/-,+
# $# '
(,(-(./

12. *+
Es una función Vectorial, donde las funciones componentes f, g y h son funciones del parámetro t.
Algunas veces, las funciones vectoriales se denotan como
Ejemplos
(,(-/-,+
(,(-(./

13. *+
2.2. ¿Cuál es la relación entre funciones vectoriales y curvas espaciales?
Hay una relación muy cercana entre funciones vectoriales continuas y curvas espaciales, las
funciones componentes de las funciones vectoriales f, g y h en un intervalo I,
conjunto de puntos C en el espacio (x, y, z) donde las funciones
hacer variar t a través del intervalo I, componen la curva espacial.
2.3. Defina f t L
lim ( ) en términos
t a
=
→
El 425678 9
:;
significa que el vector
En términos de y =
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
están compuesto por el
ε ,δ . ¿qué representa gráficamente?
9
tiende al vector :;
al
cuando t tiende a a.
Page 3

14. Sii
? @ A= ? @BCD
:DC E
Siempre que
@ E B B E
Si
@ E B B E = 7 CD
MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
El 425678 9
:;
425
678
9
:;
esta definición equivale a decir que la
longitud y la dirección del vector
longitud y la dirección del vector L
0
m2.4. Calcule el lir ( t
) t→
, donde r
425
67
9 F425
67
sent
2.5. ¿Cómo determina si una función vectorial es continua en
De acuerdo con la definición de continuidad para las funciones vectoriales que dice que una función
vectorial 9
existe cuando 7 y
y solo si cada una de sus funciones componentes es continua en t=a.
Es decir que satisface las 3 condiciones siguientes
1) A9
2) A425
678
9
3) A425
678
9
9
2.6. Defina derivada de una función vectorial y dé su interpretación
La derivada de una función vectorial se define como
G 425
H7@
H
H
Para todo t para el cual existe el límite. Si
para todo c en un intervalo abierto I, entonces
derivable en el intervalo I. La derivabilidad de funciones
vectoriales puede extenderse a intervalos cerrados
considerando límites unilaterales.
Como interpretación geométrica, tenemos que la derivada
de la función vectorial G es un vector tangen
curva dada por f(t) y que apunta en la dirección de
valores crecientes de t
2.7. ¿Qué es una curva suave?¿Cómo se encuentra el vector tangente a una curva suave en un
punto? ¿Cómo se encuentra la recta tangente? ¿Y el vector tangente unitario?
Curva suave:
La parametrización de la curva representada por la función vectorial
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
=
CD :DC E
9
se aproxima a la
( ) k
t
t t i t e j t = + + ⋅ + 3 − ( ) 1
IJ # F425
67
(K6J $# L425
67
23
M'
#'
t=a?
425678 9
9
; una función vectorial es continua en t=a si
geométrica.
G

15. existe
es
tangente a la
# $# '
Page 4

16. MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
Es suave o regular en un intervalo abierto I, si f’, g’ y h’ son continuas en I y
el intervalo I (excepto quizás en cualquier punto e
@ para todo t en
Para hallar los vectores velocidad y aceleración en un instante dado t, considérese un punto
NO HP H que se aproxima al punto
# $# , a medida que
aproxima a la dirección del movimiento en el instante t.
425
H
H
) se
Si este límite existe, se define como el vector velocidad o el vector tangente a la curva en el punto P
Sea C una curva suave en el intervalo abierto I, representada por
en t, se define como
QR
La recta tangente a una curva (trayectoria)
punto y es paralela al vector tangente unitario. Usando la forma punto
una recta (usando los números directores y las coordenadas del pu
paramétrica de la recta tangente.
2.8. Si u (t) y v (t) son funciones vectoriales que se pueden derivar,
función de valor real, escriba las reglas para derivar las siguientes funciones vectoriales.
a ) u ( t ) + v ( t ) b ) c ⋅
u ( t
)
d u t v t e u t v t
) ( ) ⋅ ( ) ) ( ) ×
( )
CHAPTER 9 – VECTOR FUNCTIONS
c f t ⋅ u t
) ( ) ( )
f u f t
– BY GERARDO
S
extremo de I.
TO Pa lo largo de la curva C dada por
H 7 @ , la dirección del vector RTRRRNR (denotado por
H
R
R H
R
H
R
R H
R
H
H
H7@
H
R
H 425
H7@
R H
R
H
. El vector unitario tangente T(t)
QR
S
U
SU
S
@
ta a una curva en un punto es la recta que pasa por ese
punto-dirección de la ecuación de
punto), obtenemos la ecuación
c es un escalar, y
) ( ( ))
Page 5
, f es una

17. MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
V)R
V [ )RS S
V )R[

18. W )RS
V W )R[ GW )R W )RS
V W [ )RGW )RW S
V [ )RG )R S
V [ GW )RS
V

19. W )
V
V)R
V)R
V)R
2.9. ¿Qué relación existe entre f
(t) y f ' (t) ?
Si es una función vectorial diferenciable en un intervalo I, y
intervalo, entonces los vectores
3. Aplicaciones físicas
3.1. ¿Cómo encuentre la velocidad, la rapidez, y la aceleración de una partícula que se desplaza a
lo largo de una curva espacial?
T+.*

20. *+,
X(-+

21. *
Y

22. (-(

23. *+,
Z/*(% U
3.2. El vector posición de un objeto que se desplaza en un plano está dado por
( ) 0 3 2 r t = t i + t j t ≥ .Encuentre su velocidad, su rapidez y su aceleración cuando
ilustre geométricamente
La velocidad, la aceleración y la rapidez
X(-+

24. *
Y

25. (-(

26. *+,
Z/*(% U
Para t = 1
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
CC es constante para todo t del
y S son ortogonales.
# $# %'
G G# G$# G'
GS GG# GS$# GS'
U U
GU ]VG[ VG[ V%G[
en un tiempo t son:
+

27. *
G ^# $#
GS 1# $#
U U
GU ]V^[ V[ ]_` a
t=1 e
Page 6

28. MMMMAAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
G ^# $#
GS 1# $# UU U
GU ]_`
3.3. ¿Cómo se conoce la posición
a k^
de una partícula si conocemos la aceleración? ¿Qué condiciones
se deben conocer para calcular la posición de la partícula?
Las integrales vectoriales se utilizan para encontrar el vector posición cuando se conocen los
vectores velocidad o aceleración
3.4. Una partícula inicia en r (0)
) = 1,0,0 con velocidad inicial v (0) = i − j + k . Su aceleración es
a(t) = 4ti + 6tj + k . Determine su velocidad y posición en el tiempo
Como la aceleración proviene de la derivada primera de la velocidad,
b
'
Para encontrar el valor de la constante del vector C, usamos el valor de la velocidad inicial que esta
definida como @ # $#, como
# ^$#
Como la velocidad es igual a la derivada primera de la posición, tenemos entonces que
b bc # ^
Para t=0, tenemos que d
@
e
3.5. Si una curva en R3 tiene aceleración cero, ¿podría decirse que la curva es una línea recta?
4. Aplicaciones geométricas
4.1. Defina vector tangente unitario, vector normal unitario y vector Binormal
Sea C una curva suave representada por
se define como
El vector tangente unitario T (t) indica la dirección de la curva
El vector normal principal o Unitario se define con lo siguiente:
CHAPTER 9 – VECTOR FUNCTIONS
– BY GERARDO
t.
tenemos entonces que
bOa# 1$#'
P # ^$# '
f
@ f; entonces f # $#'
'
# $#'
# ^ $#
^ $# '
g e
^
Ih # I
*
e
^
Ih # I $# i
j'
Binormal.
en un intervalo abierto I. El vector tangente unitario T (t)
QR
G
U
GU
.*
G
@
itario Page 7
'
$# i
j'
d

29. MAMMMAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
Sea C una curva suave representada por
en un intervalo abierto I. Si QR
G
@ el vector normal
principal en t se define como
lRR
G
CQRGC
QR
En cualquier punto de la curva, un vector normal unitario es ortogonal al vector tangente unitario.
Existe un tercer vector unitario que es perpendicular tanto a QR como a lRR es el vector Binormal mR que
se define como
mR QR lRR
como lR
Tanto QR
R y el vector Binormal mR
, son perpendiculares entre si, siguen la regla de la mano
derecha y se mueven a lo largo de la trayectoria. Juntos forman el triedo de Frenet.
4.2. Longitud de arco
4.2.a. Sea C la curva suave definida por la función vectorial continua r (t) = f (t), g(t) con
a ≤ t ≤ b . Considere además que la curva C es recorrida exactamente una vez cuando t
va del extremo a al extremo b. Deduzca la fórmula de la longitud de arco.
Como la longitud de arco de una curva dada por en el intervalo V n[ es
o b ] VG[
@
b p L
M
@
Entonces podemos escribir
b p L
M
@
b p L
q
q
M
@
bpL
q q
q
M
q
Sacamos raíz cuadrada y
o bpL
M
L
M
b]VG[ VG[
Definición:
Si C es una curva suave dada por
# $# %'
en un intervalo [a, b], entonces la
longitud de arco de C en el intervalo es
o b]VG[ VG[ V%G[
bU
RSU
4.2.b. Hallar la longitud de arco de la hélice circular con ecuación vectorial
r (t) = cos ti + sentj + tk desde el punto (1,0,0) hasta (1,0,2π)
La derivada primera de
es igual a:
S .(,*#

30. +.r#'
U
SU ].(,

31. +. k
El arco desde (1, 0, 0) hasta (1, 0, 2π) se describe para el intervalo del parámetro @ s
CHAPTER 9 – VECTOR FUNCTIONS – BY GERARDO Page 8

32. MAMMMAAATTTTHHHHEEEEMMMMAAAATTTTIIIICCCCSSSS
o bU
RSU
s
b ]
@
]s
4.2.c. Defina función longitud de arco
Sea C una curva suave dada por
definida en el intervalo cerrado [a, b]. Para , la
función longitud de arco está dada por
o bU
RS)U)
b]VG)[ VG)[ V%G)[
)
A la longitud de arco S se le llama parámetro longitud de arco
CHAPTER 9 – VECTOR FUNCTIONS – BY GERARDO Page 9