Trigonometria
•Télécharger en tant que PPT, PDF•
0 j'aime•172 vues
PPT sobre las razones trigonométricas
Signaler
Partager
Signaler
Partager
Recommandé
Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE) at the 2nd Baltic Maritime Spatial Planning Forum in Riga, Latvia on 23-24 November 2016 (the final conference of the Baltic SCOPE collaboration).
Speakers:
** Michael Kull and Andrea Morf, Baltic SCOPE lessons learned, Senior Research Fellows at Nordregio (Nordic Centre for Spatial Development)
** Riku Varjopuro, Baltic SCOPE monitoring & evaluation framework, Head of unit at the Finnish Environment Institute, Environmental Policy Centre, Interactive Governance Unit
** Anni Konsap,Advisor of the Planning Department at the Estonian Ministry of Finance
** Jan Schmidtbauer Crona, Senior Analyst at Swedish Agency of Marine and Water Management
** Wesley Flannery, Lecturer in the School of Planning, Architecture and Civil Engineering (SPACE) and Institute of Environmental and Spatial Planning (ISEP) at Queen’s University, Belfast
Video and other presentations - www.balticscope.eu
www.vasab.orgObstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...

Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...Pan Baltic Scope / Baltic SCOPE
Contenu connexe
Tendances
Tendances (15)
Pontificia universidad católica del ecuador sede ibarra

Pontificia universidad católica del ecuador sede ibarra
En vedette
Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE) at the 2nd Baltic Maritime Spatial Planning Forum in Riga, Latvia on 23-24 November 2016 (the final conference of the Baltic SCOPE collaboration).
Speakers:
** Michael Kull and Andrea Morf, Baltic SCOPE lessons learned, Senior Research Fellows at Nordregio (Nordic Centre for Spatial Development)
** Riku Varjopuro, Baltic SCOPE monitoring & evaluation framework, Head of unit at the Finnish Environment Institute, Environmental Policy Centre, Interactive Governance Unit
** Anni Konsap,Advisor of the Planning Department at the Estonian Ministry of Finance
** Jan Schmidtbauer Crona, Senior Analyst at Swedish Agency of Marine and Water Management
** Wesley Flannery, Lecturer in the School of Planning, Architecture and Civil Engineering (SPACE) and Institute of Environmental and Spatial Planning (ISEP) at Queen’s University, Belfast
Video and other presentations - www.balticscope.eu
www.vasab.orgObstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...

Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...Pan Baltic Scope / Baltic SCOPE
En vedette (19)
An Introduction to Fish Conservation Zone Assessments

An Introduction to Fish Conservation Zone Assessments
Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...

Obstacles and enablers in transboundary planning collaboration (Baltic SCOPE)...
Similaire à Trigonometria
Similaire à Trigonometria (20)
C:\documents and settings\user1\escritorio\geometriasegblok1

C:\documents and settings\user1\escritorio\geometriasegblok1
Dernier
Centros Multigrados Procedimientos para la planificación en los Centros Educativos tipo V ( multi...

Procedimientos para la planificación en los Centros Educativos tipo V ( multi...Katherine Concepcion Gonzalez
Dernier (20)
🦄💫4° SEM32 WORD PLANEACIÓN PROYECTOS DARUKEL 23-24.docx

🦄💫4° SEM32 WORD PLANEACIÓN PROYECTOS DARUKEL 23-24.docx
PLAN LECTOR 2024 integrado nivel inicial-miercoles 10.pptx

PLAN LECTOR 2024 integrado nivel inicial-miercoles 10.pptx
Prueba de evaluación Geografía e Historia Comunidad de Madrid 4ºESO

Prueba de evaluación Geografía e Historia Comunidad de Madrid 4ºESO
Desarrollo y Aplicación de la Administración por Valores

Desarrollo y Aplicación de la Administración por Valores
Procedimientos para la planificación en los Centros Educativos tipo V ( multi...

Procedimientos para la planificación en los Centros Educativos tipo V ( multi...
Plan-de-la-Patria-2019-2025- TERCER PLAN SOCIALISTA DE LA NACIÓN.pdf

Plan-de-la-Patria-2019-2025- TERCER PLAN SOCIALISTA DE LA NACIÓN.pdf
Código Civil de la República Bolivariana de Venezuela

Código Civil de la República Bolivariana de Venezuela
Louis Jean François Lagrenée. Erotismo y sensualidad. El erotismo en la Hist...

Louis Jean François Lagrenée. Erotismo y sensualidad. El erotismo en la Hist...
Prueba de evaluación Geografía e Historia Comunidad de Madrid 2º de la ESO

Prueba de evaluación Geografía e Historia Comunidad de Madrid 2º de la ESO
UNIDAD DIDACTICA nivel inicial EL SUPERMERCADO.docx

UNIDAD DIDACTICA nivel inicial EL SUPERMERCADO.docx
La Sostenibilidad Corporativa. Administración Ambiental

La Sostenibilidad Corporativa. Administración Ambiental
Ensayo Paes competencia matematicas 2 Preuniversitario

Ensayo Paes competencia matematicas 2 Preuniversitario
Trigonometria
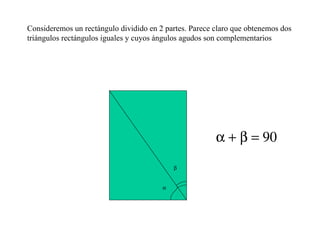
- 1. Consideremos un rectángulo dividido en 2 partes. Parece claro que obtenemos dos triángulos rectángulos iguales y cuyos ángulos agudos son complementarios
- 2. Si separamos y giramos los triángulos de modo que los veamos para medir ángulos, nos damos cuenta de que el cateto opuesto a es el mismo que el cateto contiguo a
- 4. Consideremos ahora el caso de un ángulo mayor que 90º y su suplementario El ángulo define un seno y un coseno sobre la circunferencia goniométrica sen cos Pero fijémonos en la otra parte del ángulo (el suplementario). Superpongamos un triángulo para verlo mejor Tras girar el triángulo lo hemos colocado para medir correctamente su seno y su coseno. Como los lados no ha cambiado durante el giro, vemos que los valores coinciden con los del ángulo salvo por el signo del coseno (que está en distinto cuadrante
- 6. Consideremos ahora un triángulo rectángulo sobre la circunferencia goniométrica. Este triángulo definirá unas razones trigonométricas. cos sen Si giramos el triángulo hasta que formen dos ángulos opuestos por el vértice, obtenemos una construcción en la que los senos y los cosenos de los ángulos sólo serán distintos en signo cos sen
- 7. Como los ángulos y se diferencian en 180 º podemos escribir cos sen cos sen sen (180 + sen cos (180 + cos Las razones de ángulos que se diferencian en 180º tienen sus signos opuestos
- 8. cos sen cos sen Consideremos ahora un triángulo sobre la circunferencia goniométrica al cual vamos a aplicar una simetría respecto del eje horizontal. Es claro que las nuevas razones trigonométricas que definimos tendrán el mismo valor que las originales pero con el signo del seno opuesto. Por lo tanto Las razones trigonométricas de ángulos cuya suma es el ángulo completo sólo se diferencian en el signo del seno sen (360 - sen cos (360 - cos