Universidad Tecnológica de Panamá Centro Regional de Chiriquí
CAPÍTULO 2
ESTÁTICA DE PARTÍCULAS
2. 1 Definición de Fuerza
La fuerza es un vector por lo que podemos aplicar los métodos para operaciones de vectores conocidos.
2.2 Métodos para Suma de Vectores
a. Métodos
Gráficos
Los métodos gráficos requieren trazar los vectores a escala y utilizar regla y transportador para indicar
dirección y módulo. El método del Paralelogramo se emplea para sumar sólo dos vectores y el método del
polígono (o poligonal) para sumar dos o más vectores.
Método del Paralelogramo: Consiste en colocar los vectores de forma que coincidan los puntos de
aplicación de los dos vector y formar un paralelogramo con la proyección de estos vectores en los lados
opuestos. El vector suma ( Resultante R ) se obtendrá de la diagonal del paralelogramo que se ha formado.
Ing. Cynthia Samudio Mecánica1
Una fuerza representa la acción de un cuerpo sobre otro y, generalmente, está caracterizada por su punto
de aplicación, su magnitud y su dirección.
Clasificación de los
métodos para
sumar vectores
Métodos Gráficos
Métodos Analíticos
Método del Paralelogramo
Método del Polígono
Método de Componentes
Rectangulares
Método del Triángulo
Módulo
Figura 1. Representación de un vector Fuerza

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
Método del Polígono. Consiste en colocar los vectores uno a continuación del otro y así sucesivamente
hasta que todos los vectores estén presentes. El vector suma (Resultante) se obtiene trazando el vector que va
del origen del primero al extremo del último vector.
b. Métodos Analíticos
Los métodos analíticos son el método de componentes para 2 o más vectores y el método del triángulo (una
variación del método poligonal donde se requiere emplear métodos trigonométricos para resolver las
incógnitas) para dos vectores.
Método del Triángulo
Se aplica el método del polígono (un vector a continuación del otro) y luego se trabaja con le triángulo que se
forma al trazar la resultante.
Ing. Cynthia Samudio Mecánica2
Como se observa en la figura 1.
Los vectores A y B se colocan de
forma que coinciden sus puntos
de aplicación.
Figura 3. Método del Paralelogramo
Figura 3. Método del Polígono
Figura 4. Método del Triángulo

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
Si el triángulo es rectángulo:
Se pueden aplicar las funciones trigonométricas y el teorema de Pitágoras para determinar la resultante y el
ángulo que nos indica su dirección.
Si el triángulo es oblicuo (Un triángulo oblicuo es cualquier triángulo que no sea recto)
Para poder obtener la Resultante y su dirección debe obtenerle por medio de la ley de cosenos y la ley de los
senos enunciadas a continuación.
Ley de los Cosenos : te permite encontrar cualquier lado de un triángulo, si conoces los otros dos y el
ángulo opuesto al lado que quieres determinar.
Ley de los Senos
En cualquier triángulo se verifica que las longitudes de los lados son proporcionales a los senos de los
ángulos opuestos. Expresado en función del triángulo de la figura
Ing. Cynthia Samudio Mecánica3
Funciones Trigonométricas
Sen A= lado opuesto/hipotenusa = a/c
Cos A = lado adyacente/hipotenusa= b/c
Tan A= lado opuesto/lado adyacente=a/B
Teorema de Pitágoras
R2
= A2
+ B2
Figura 5. Triángulo Rectángulo
a2
= b2
+ c2
- 2bc cos α
b2
= a2
+ c2
- 2ac cos β
c2
= a2
+ b2
- 2ab cos γ
Figura 6. Triángulo Oblicuo

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
Método de los Componentes
Cualquier fuerza que actúa sobre una partícula se puede descomponer en dos o más componentes, esto es,
puede ser reemplazada por dos o más fuerzas que originen el mismo efecto sobre la partícula.
Pasos para Aplicar el Método de las Componentes
1-Dibuje todos los vectores a partir del origen en un sistema coordenado
2.-Descomponga todos los vectores en sus componentes "X" y "Y". (Nota: Recuerde tomar en cuenta la
dirección negativa o positiva de los componentes)
3.-Encuentre la componente "X" de la resultante sumando los componentes "X" de todos los vectores.
Rx= Ax+Bx+Cx+.....
4.-Encuentre la componente "Y" de la resultante sumando los componentes "Y" de los vectores.
Ry= Ay+By+Cy+......
5.-Obtenga la magnitud y dirección de la resultante a partir de dos vectores perpendiculares, aplicando el
teorema de Pitágoras y la función trigonométrica tangente.
Ing. Cynthia Samudio Mecánica4
x
y
Fy
Fx
Se dice que una fuerza se ha
descompuesto en dos componentes
rectangulares si sus componentes Fx
y Fy son perpendiculares entre sí y
están dirigidos a los largo de los ejes
coordenados
Figura 7. Triángulo Oblicuo.
Figura 8. Componentes Fx y Fy del vector F.
F

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
En la Figura 9 se observa la coexistencia de los vectores A, B y C. El vector resultante se obtiene a través del
Método de los Componentes; observe la manera en que se obtienen las proyecciones de cada vector: se
descomponen rectangularmente
Empleando Vectores Unitarios
Otra forma de sumar vectores utilizando las componentes rectangulares es usar los vectores unitarios para
representar la dirección de las componentes en sus ejes x, y y z.
Para poder representar cada vector en este sistema de coordenadas cartesianas, haremos uso de tres vectores
unitarios. Estos vectores unitarios, son unidimensionales, esto es, tienen módulo 1, son perpendiculares entre
sí y corresponderán a cada uno de los ejes del sistema de referencia.
Se usan los símbolos i,j, y k para representar los componentes en x, y y z respectivamente.
Ing. Cynthia Samudio Mecánica5
Figura 9. Descomposición de vectores

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
Los vectores puede escribirse así:
F= Fxi + Fyj + Fzk
Donde Fx, Fy y Fz son los componentes de un vector fuerza.
Para sumar dos o más, se suman las componentes en x, y y z. Por
ejemplo
R=(Ax +Bx)i+(Ay+By)j+(Az+Bz)k
2.3 Operaciones con Vectores. Producto Punto. Producto Cruz.
a. Producto Punto o Escalar
Dado dos vectores A y B, se define el producto escalar de ellos al número real dado por la ecuación:
αcosbaba =⋅
siendo ∝ el ángulo que los relaciona.. El producto punto se representa por un punto ( · ) y su resultado es un
número (escalar).
Teniendo en cuenta que el producto escalar de los vectores :
i · i = 1; j· j = 1; k · k = 1
Y cualquier otro producto es igual a cero el resultado de multiplicar escalarmente a por b es:
a · b = ax· bx + ay · by+ az · bz
En el cuadro podemos apreciar el resultado de aplicar el producto punto a los vectores unitarios
. i j k
i 1 0 0
j 0 1 0
k 0 0 1
El producto escalar se aplica para determinar.
a. ángulo entre dos vectores.
b. La proyección de un vector sobre otro.
Ing. Cynthia Samudio Mecánica6
Figura 10. Vectores Unitarios

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
c. La perpendicularidad entre vectores (Si el resultado del producto punto es 0, los vectores son
perpendiculares)
Producto Cruz o Producto Vectorial
El producto cruz de dos vectores (A y B en la figura) contenidos en un mismo plano es igual a un vector
perpendicular al mismo. El producto cruz se representa por una exe (X) y su resultado es un vector.La
dirección de ese vector se establece utilizando la regla de la mano derecha. Dicha regla dice que los dedos de
la mano derecha giran desde A hasta B siguiendo el camino más corto, y el pulgar indica la dirección del C.
De forma más sencilla podemos aplicar el siguiente procedimiento.
La dirección de la flecha indica el sentido positivo del producto cruz si
multiplicamos i X j el resultado será k, si multiplicamos kX i el resultados será j.
Por el contrario si nos movemos en sentido contrario al indicado entonces la
respuesta será negativa. j X i = -k y k X j = -i
Es importante recalcar que no se puede calcular el producto cruz de dos vectores con un ángulo de 0º entre sí,
porque la respuesta será 0 decir i x i =0, j x j = 0 y k x k =0
El siguiente cuadro presenta un resumen del producto vectorial para vectores unitarios-
Ing. Cynthia Samudio Mecánica7
Figura 11. Producto Cruz
j
k i
+

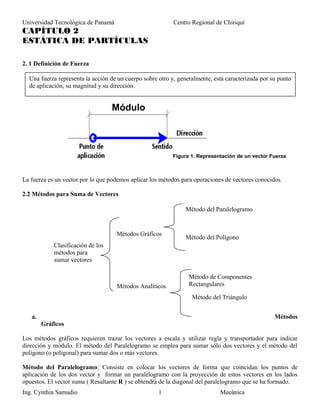
Universidad Tecnológica de Panamá Centro Regional de Chiriquí
X i j k
i 0 k -j
j -k 0 i
k j -i 0
2.4 Componentes de una fuerza en el espacio tridimensional
a. Empleando los cosenos directores
Una fuerza en el espacio tridimensional se puede descomponer en componentes rectangulares Fx, Fy y Fz.
Denotando por xθ , yθ y zθ , los ángulos que F forma, respectivamente con los ejes x, y y z (figura )., se
tiene entonces que.
xx FF θcos=
Los cosenos de xθ , yθ y zθ , se conocen como los cosenos directores de la fuerza F. Expresando la Fuerza
en función de los vectores unitarios
Ing. Cynthia Samudio Mecánica8
yy FF θcos= zz FF θcos=
kFjFiFF zyx ++=
Figura 12. Cosenos directores

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
También se puede expresar en función de los cosenos directores de forma que
Lo cual demuestra que F es el producto de su magnitud F y el vector unitario
Como la magnitud de λ es igual a la unidad, se debe cumplir que
Cuando las componentes rectangulares Fx, Fy y Fz de una fuerza F son conocidas, la magnitud F de la fuerza
se encuentra escribiendo
Y los cosenos directores de F se obtienen a partir de las ecuaciones ()
F
F
F
F
F
F z
z
y
y
x
x === θθθ coscoscos
b. Conocido la magnitud de la Fuerza y los ángulos yθ y Φ
En caso de que la fuerza este expresada en función del ángulo yθ y del ángulo Φ (ángulo que se forma entre
el eje x y el plano que contiene la fuerza F (figura ). Entonces empleando el ángulo yθ podemos encontrar
Fy y la componente horizontal Fh. Con Fh y el ángulo Φ encontramos Fx y Fz aplicando funciones
trigonométricas.
Las componentes escalares son:
Fy = F cos yθ
Fh= F sen yθ
Fx = Fh cos Ф
Fz = Fh sen Ф
Sustituyendo en (3) y (4) el valor de Fh
Fy = F cos yθ
Fx = Fh cos Ф =F sen yθ cos Ф
Fz = Fh sen Ф= F sen yθ sen Ф
Ing. Cynthia Samudio Mecánica9
)coscos(cos kjiFF zyx θθθ ++=
kji zyx θθθλ coscoscos ++=
1coscoscos 222
=++ zyx θθθ
222
zyx FFFF ++=
x
z
y
F
B
A
C
O
Ф
Θ
y
Fy
Fh
Fx
Fz

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
c. Conocida la magnitud de la Fuerza y dos puntos a lo largo de su línea de acción
Sean los puntos M y N a lo largo de la línea de acción de la fuerza F para obtener sus componentes
rectangulares. Primero, se expresa el vector MN .
2.3 Equilibrio de una Partícula
Es decir que si al sumar los vectores obtenemos como resultado que la resultante sea igual a cero, se dice que
el cuerpo está en equilibrio.
∑ == 0FR
0=∑ xF 0=∑Fy
Expresadas en vectores unitarios:
( ) 0)( =+= ∑∑ jFyiFxR
º
Ing. Cynthia Samudio Mecánica10
Cuando la resultante de todas las fuerzas que actúan sobre una partícula es
igual a cero, la partícula está en equilibrio.

Universidad Tecnológica de Panamá Centro Regional de Chiriquí
CLAVES PARA RESOLVER PROBLEMAS DE EQUILIBRIO DE UNA PARTICULA
Debe dibujar un diagrama de cuerpo libre claro y preciso para resolver cualquier problema de equilibrio.
Recuerde tomar adecuadamente la dirección de la fuerza según sea el elemento del problema.
Ing. Cynthia Samudio Mecánica11