Retail sale Time Series

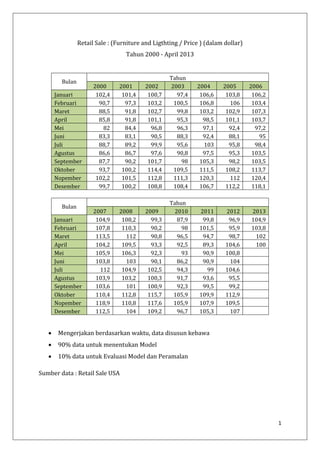
1
Retail Sale : (Furniture and Ligthting / Price ) (dalam dollar)
Tahun 2000 - April 2013
Bulan
Tahun
2000 2001 2002 2003 2004 2005 2006
Januari 102,4 101,4 100,7 97,4 106,6 103,8 106,2
Februari 90,7 97,3 103,2 100,5 106,8 106 103,4
Maret 88,5 91,8 102,7 99,8 103,2 102,9 107,3
April 85,8 91,8 101,1 95,3 98,5 101,1 103,7
Mei 82 84,4 96,8 96,3 97,1 92,4 97,2
Juni 83,3 83,1 90,5 88,3 92,4 88,1 95
Juli 88,7 89,2 99,9 95,6 103 95,8 98,4
Agustus 86,6 86,7 97,6 90,8 97,5 95,3 103,5
September 87,7 90,2 101,7 98 105,3 98,2 103,5
Oktober 93,7 100,2 114,4 109,5 111,5 108,2 113,7
Nopember 102,2 101,5 112,8 111,3 120,3 112 120,4
Desember 99,7 100,2 108,8 108,4 106,7 112,2 118,1
Bulan
Tahun
2007 2008 2009 2010 2011 2012 2013
Januari 104,9 108,2 99,3 87,9 99,8 96,9 104,9
Februari 107,8 110,3 90,2 98 101,5 95,9 103,8
Maret 113,5 112 90,8 96,5 94,7 98,7 102
April 104,2 109,5 93,3 92,5 89,3 104,6 100
Mei 105,9 106,3 92,3 93 90,9 100,8
Juni 103,8 103 90,1 86,2 90,9 104
Juli 112 104,9 102,5 94,3 99 104,6
Agustus 103,9 103,2 100,3 91,7 93,6 95,5
September 103,6 101 100,9 92,3 99,5 99,2
Oktober 110,4 112,8 115,7 105,9 109,9 112,9
Nopember 118,9 110,8 117,6 105,9 107,9 109,5
Desember 112,5 104 109,2 96,7 105,3 107
 Mengerjakan berdasarkan waktu, data disusun kebawa
 90% data untuk menentukan Model
 10% data untuk Evaluasi Model dan Peramalan
Sumber data : Retail Sale USA

2
1) Gambarkan Data berdasarkan waktunya
Berdasarkan Plot diatas, dapat disimpulkan bahwa data tidak stasioner sacara
rata-rata dan variansi. Maka perlu dilakukan Transformasi dan Differensing.
2) a. Lakukan Transformasi Box-Cox
Dapat dilihat bahwa Rouded Value adalah 0,50. Maka Transformasi yang
digunakan adalah ln 𝑍𝑡
140126112988470564228141
120
110
100
90
80
Index
C2
Time Series Plot of C2
5,02,50,0-2,5-5,0
4,6
4,5
4,4
4,3
4,2
Lambda
StDev
Lower CL Upper CL
Limit
Estimate 0,05
Lower CL -1,57
Upper CL 1,91
Rounded Value 0,00
(using 95,0% confidence)
Lambda
Box-Cox Plot of C2

3
b. Gambarkan data setelah di Transformasi
Karena dari gambar tersebut dapat dilihat bahwa masih tetap tidak stasioner
secara mean dan varians. Maka langkah selanjutnya adalah melakukan
differensing.
3) Lakukan Differensing dengan Ordo 1
Plot C4 menunjukkan data yang di differensing 1kali, terlihat bahwa data sudah
cukup stasioner. Untuk itu kita dapat melakukan langkah selanjutnya
140126112988470564228141
4,8
4,7
4,6
4,5
4,4
Index
C3
140126112988470564228141
0,15
0,10
0,05
0,00
-0,05
-0,10
-0,15
-0,20
-0,25
Index
C4

4
4) Uji tambahan Dickey Fuller
Untuk melihat apakah data telah stasioner atau tidak, dapat dilakukan dengan cara
lain, yaitu melalui Eviews, dengan uji Dickey Fuller
 Data awal
Null Hypothesis: SER01 has a unit root
Exogenous: Constant
Lag Length: 12 (Automatic based on SIC, MAXLAG=13)
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -1.993609 0.2894
Test critical values: 1% level -3.481217
5% level -2.883753
10% level -2.578694
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(SER01)
Method: Least Squares
Date: 06/24/13 Time: 18:44
Sample (adjusted): 14 143
Included observations: 130 after adjustments
Variable Coefficient Std. Error t-Statistic Prob.
SER01(-1) -0.170115 0.085330 -1.993609 0.0485
D(SER01(-1)) -0.163775 0.110994 -1.475529 0.1428
D(SER01(-2)) -0.154182 0.110083 -1.400596 0.1640
D(SER01(-3)) -0.090563 0.106143 -0.853218 0.3953
D(SER01(-4)) -0.144777 0.101917 -1.420533 0.1581
D(SER01(-5)) -0.146298 0.097884 -1.494616 0.1377
D(SER01(-6)) -0.283717 0.096028 -2.954528 0.0038
D(SER01(-7)) -0.194586 0.093153 -2.088893 0.0389
D(SER01(-8)) -0.205338 0.091153 -2.252668 0.0262
D(SER01(-9)) -0.178674 0.089713 -1.991630 0.0488
D(SER01(-10)) -0.302353 0.088684 -3.409323 0.0009
D(SER01(-11)) -0.060224 0.089666 -0.671649 0.5031
D(SER01(-12)) 0.370274 0.086042 4.303415 0.0000
C 17.40466 8.643782 2.013547 0.0464
R-squared 0.513832 Mean dependent var 0.061538
Adjusted R-squared 0.459348 S.D. dependent var 6.230276
S.E. of regression 4.581062 Akaike info criterion 5.983179
Sum squared resid 2434.391 Schwarz criterion 6.291991
Log likelihood -374.9066 F-statistic 9.430833
Durbin-Watson stat 2.111776 Prob(F-statistic) 0.000000

5
Nilai Probabilitas adalah 0,2849 artinya lebih besar dari 0,05 maka data tidak
stasioner dan dapat dilakukan differensing
 Dengan 1kali differensing
Null Hypothesis: D(SER01) has a unit root
Exogenous: Constant
Lag Length: 11 (Automatic based on SIC, MAXLAG=13)
t-Statistic Prob.*
Augmented Dickey-Fuller test statistic -4.616004 0.0002
Test critical values: 1% level -3.481217
5% level -2.883753
10% level -2.578694
*MacKinnon (1996) one-sided p-values.
Augmented Dickey-Fuller Test Equation
Dependent Variable: D(SER01,2)
Method: Least Squares
Date: 06/24/13 Time: 18:47
Sample (adjusted): 14 143
Included observations: 130 after adjustments
Variable Coefficient Std. Error t-Statistic Prob.
D(SER01(-1)) -3.372824 0.730681 -4.616004 0.0000
D(SER01(-1),2) 2.066808 0.679534 3.041509 0.0029
D(SER01(-2),2) 1.783721 0.618424 2.884301 0.0047
D(SER01(-3),2) 1.577577 0.558512 2.824608 0.0056
D(SER01(-4),2) 1.330523 0.498584 2.668602 0.0087
D(SER01(-5),2) 1.096251 0.439329 2.495285 0.0140
D(SER01(-6),2) 0.736335 0.378900 1.943349 0.0544
D(SER01(-7),2) 0.482208 0.321631 1.499258 0.1365
D(SER01(-8),2) 0.231578 0.264061 0.876988 0.3823
D(SER01(-9),2) 0.020597 0.206539 0.099722 0.9207
D(SER01(-10),2) -0.303023 0.146375 -2.070182 0.0406
D(SER01(-11),2) -0.369868 0.087128 -4.245090 0.0000
C 0.191150 0.408819 0.467566 0.6410
R-squared 0.758538 Mean dependent var 0.011538
Adjusted R-squared 0.733773 S.D. dependent var 8.990655
S.E. of regression 4.638928 Akaike info criterion 6.001483
Sum squared resid 2517.800 Schwarz criterion 6.288237

6
Log likelihood -377.0964 F-statistic 30.62902
Durbin-Watson stat 2.096270 Prob(F-statistic) 0.000000
Nilai Probabilitas adalah 0,0002 artinya nilai lebih kecil dari 0,05 maka data
sudah stasioner. Maka dapat dilakukan langkah selajutnya.
5) Lakukan Identifikasi ACF dan PACF
Plot C4 menunjukan ACF yang berpola Eksponensial dan seasonal di lag 12. Dan
Plot C4 menunjukkan PACF yang berpola Cut-Off .
1009080706050403020101
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation
Autocorrelation Function for C4
(with 5% significance limits for the autocorrelations)
1009080706050403020101
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
PartialAutocorrelation
Partial Autocorrelation Function for C4
(with 5% significance limits for the partial autocorrelations)

7
 Oleh karena data diatas merupakan Data Seasonal, maka data tidak bisa
langsung di Estimasi. Dan harus dilakukan Differensing sebanyak seasonalnya
dan hasilnya merupakan Zt.
6) Plot Data Zt yang merupakan hasil differensing sebanyak Seasonal
Plot Zt menunjukkan plot data yang sudah didifferensing sebanyak 12 kali. Plot ini
untuk menghilangkan seasonalnya.
7) Memunculkan ACF dan PACF
Berdasarkan Plot diatas terlihat bahwa ACF berpola Cut-Off dan PACF berpola Cut
di lag ke-1. Karena ACF dan PACF Cut-Off maka model yang digunakan AR atau MA
dengan 1kali differensing.
140126112988470564228141
0,3
0,2
0,1
0,0
-0,1
-0,2
Index
C5
Zt
1009080706050403020101
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation
Autocorrelation Function for C5
1009080706050403020101
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
PartialAutocorrelation
Partial Autocorrelation Function for C5
(with 5% significance limits for the partial autocorrelations)

8
8) Estimasi Parameter
Karena ACF dan PACF berpola Cut-Off maka Model yang digunakan Model ARI atau
IMA. Dan Model yang memungkinkan adalah:
 Zt  (1,1,0)(1,1,0)12
Estimates at each iteration
Iteration SSE Parameters
0 1,33822 0,100 0,100 0,082
1 0,46058 -0,050 -0,031 0,026
2 0,35298 -0,124 -0,181 0,013
3 0,30287 -0,211 -0,331 0,004
4 0,28749 -0,308 -0,470 -0,001
5 0,28623 -0,330 -0,541 -0,000
6 0,28603 -0,345 -0,520 -0,000
7 0,28603 -0,345 -0,519 -0,000
8 0,28603 -0,345 -0,519 -0,000
Relative change in each estimate less than 0,0010
Final Estimates of Parameters
Type Coef SE Coef T P
AR 1 -0,3448 0,0840 -4,11 0,000
SAR 12 -0,5186 0,0896 -5,79 0,000
Constant -0,000095 0,004104 -0,02 0,982
Differencing: 1 regular, 1 seasonal of order 12
Number of observations: Original series 144, after differencing 131
Residuals: SS = 0,282225 (backforecasts excluded)
MS = 0,002205 DF = 128
Modified Box-Pierce (Ljung-Box) Chi-Square statistic
Lag 12 24 36 48
Chi-Square 14,7 35,3 47,5 54,4
DF 9 21 33 45
P-Value 0,099 0,026 0,049 0,158
Uji Residual dan Normalitas
3330272421181512963
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation
ACF of Residuals for C3

9
 Zt  (1,1,0)(0,1,1)12
0 1,68505 0,100 0,100 0,091
1 0,52401 -0,050 0,179 0,032
2 0,32562 -0,143 0,329 0,010
3 0,26988 -0,209 0,479 0,003
4 0,24499 -0,256 0,629 0,000
5 0,22882 -0,291 0,779 -0,000
6 0,22546 -0,299 0,831 -0,000
7 0,22526 -0,296 0,841 -0,000
8 0,22524 -0,294 0,843 -0,000
9 0,22524 -0,294 0,844 -0,000
AR 1 -0,2943 0,0838 -3,51 0,001
SMA 12 0,8443 0,0726 11,63 0,000
Constant -0,0001885 0,0007732 -0,24 0,808
MS = 0,001522 DF = 128
Lag 12 24 36 48
Chi-Square 14,6 25,7 35,8 43,6
DF 9 21 33 45
P-Value 0,103 0,220 0,340 0,530
0,20,10,0-0,1-0,2
99,9
99
95
90
80
70
60
50
40
30
20
10
5
1
0,1
RESI1
Percent
Mean 0,00009038
StDev 0,04659
N 131
KS 0,050
P-Value >0,150
Probability Plot of RESI1
Normal

10
 Zt  (0,1,1)(0,1,1)12
0 2,31261 0,100 0,100 0,101
1 0,43685 0,250 0,232 -0,019
2 0,29675 0,299 0,382 -0,006
3 0,26228 0,342 0,532 -0,002
4 0,24636 0,393 0,662 0,000
5 0,24605 0,388 0,683 -0,000
Unable to reduce sum of squares any further
MA 1 0,3879 0,0812 4,78 0,000
SMA 12 0,6828 0,0690 9,90 0,000
3330272421181512963
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation
0,100,050,00-0,05-0,10-0,15-0,20
99,9
99
95
90
80
70
60
50
40
30
20
10
5
1
0,1
RESI2
Percent
Mean 0,0007468
StDev 0,03870
N 131
KS 0,067
P-Value >0,150
Normal

11
Constant -0,0000273 0,0008538 -0,03 0,975
MS = 0,001885 DF = 128
Lag 12 24 36 48
Chi-Square 10,1 19,6 28,1 34,2
DF 9 21 33 45
P-Value 0,344 0,549 0,708 0,879
3330272421181512963
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation
0,150,100,050,00-0,05-0,10-0,15-0,20
99,9
99
95
90
80
70
60
50
40
30
20
10
5
1
0,1
RESI3
Percent
Mean 0,001442
StDev 0,04305
N 131
KS 0,062
P-Value >0,150
Normal

12
 Zt  (0,1,1)(1,1,0)12
0 1,74163 0,100 0,100 0,091
1 0,39437 -0,050 0,203 0,016
2 0,32648 -0,200 0,248 0,008
3 0,29102 -0,350 0,310 0,002
4 0,28096 -0,480 0,382 -0,000
5 0,28004 -0,501 0,405 -0,000
6 0,27999 -0,510 0,410 -0,000
7 0,27999 -0,511 0,412 -0,000
8 0,27999 -0,512 0,413 -0,000
9 0,27999 -0,512 0,413 -0,000
SAR 12 -0,5116 0,0881 -5,81 0,000
MA 1 0,4127 0,0804 5,13 0,000
Constant -0,000230 0,002385 -0,10 0,923
MS = 0,002157 DF = 128
Lag 12 24 36 48
Chi-Square 13,8 36,6 46,1 55,0
DF 9 21 33 45
P-Value 0,129 0,019 0,064 0,147
Uji ACF Residual dan Normalitas
3330272421181512963
1,0
0,8
0,6
0,4
0,2
0,0
-0,2
-0,4
-0,6
-0,8
-1,0
Lag
Autocorrelation

13
Tabel :
Model Signifikansi Residual Acak Normal Nilai MS
(1,1,0)(1,1,0)^12 Ya Tidak Ya 0,002205
(1,1,0)(0,1,1)^12 Ya Ya Ya 0,001522
(0,1,1)(0,1,1)^12 Ya Ya Ya 0,001885
(0,1,1)(1,1,0)^12 Ya Tidak Ya 0,002157
Note : Nilai Signifikansi diperoloeh dari nilai P pada minitab, jika P < 0,05 maka data Signifikan.
Data Residual acak = Jika pada Plot Residual ACF tidak ada lag yang keluar dari garis merah.
Data Normal = Jika nilai P-Value > 0.05
Kita pilih Model yang memiliki nilai MS terkecil. Jadi model yang paling baik
digunakan adalah Model (1,1,0)(0,1,1)^12, dengan:
AR 1 : -0,2943
SMA 12 : 0,8443
Constant : -0,0001885
Maka didapat persamaan untuk model SARIMA (𝟏, 𝟏, 𝟎)(𝟎, 𝟏, 𝟏) 𝟏𝟐
𝒀𝒕 = 𝒀𝒕−𝟏 − 𝒀𝒕−𝟏𝟐 + 𝒀𝒕−𝟏𝟑 + 𝒂𝒕 − 𝟎, 𝟖𝟒𝟒𝟑𝒂𝒕−𝟏𝟐
0,20,10,0-0,1-0,2
99,9
99
95
90
80
70
60
50
40
30
20
10
5
1
0,1
RESI4
Percent
Mean 0,0001590
StDev 0,04608
N 131
KS 0,056
P-Value >0,150
Normal

14
9) Evaluasi Model dengan nilai MAPE
No At Forecast Ft (Exp At) |Ft-At| |(Ft-At)/At|
1 96,9 4,586024551 98,1036479 1,203647888 0,01242155
2 95,9 4,59562086 99,0496124 3,149612363 0,03284267
3 98,7 4,582057378 97,7152247 0,984775318 0,00997746
4 104,6 4,548477039 94,4883965 10,11160346 0,09666925
5 100,8 4,529554197 92,7172183 8,082781723 0,08018633
6 104 4,493906223 89,4702549 14,52974507 0,13970909
7 104,6 4,573010209 96,8351656 7,764834395 0,0742336
8 95,5 4,542686616 93,9428498 1,557150216 0,01630524
9 99,2 4,565594752 96,1197445 3,080255546 0,03105096
10 112,9 4,66993646 106,690963 6,209036902 0,0549959
11 109,5 4,687949496 108,630205 0,869795428 0,00794334
12 107 4,637919897 103,329189 3,670811498 0,03430665
13 104,9 4,574488237 96,9783965 7,921603513 0,07551576
14 103,8 4,58173067 97,6833056 6,116694431 0,05892769
15 102 4,568671447 96,415931 5,584069033 0,05474577
16 100 4,53475417 93,200601 6,799398993 0,06799399
Jumlah 0,84782525
𝑴𝑨𝑷𝑬 =
𝟏𝟎𝟎
𝑵
∑ |
𝑭𝒕 − 𝑨𝒕
𝑨𝒕
|
𝒏
𝒕=𝟏
=
𝟏𝟎𝟎
𝟏𝟔
∙ 𝟎, 𝟖𝟒𝟕𝟖𝟐𝟓𝟐𝟓𝟐𝟓 = 𝟓, 𝟐𝟗𝟖𝟗𝟎𝟕𝟕𝟗
∴ 𝑴𝑨𝑷𝑬 = 𝟓. 𝟐𝟗 %
10) Lakukan Peramalan
No At Forecast Ft
1 96,9 4,515742 91,44539
2 95,9 4,479932 88,22865
3 98,7 4,558895 95,47792
4 104,6 4,528424 92,61252
5 100,8 4,551187 94,74482
6 104 4,655383 105,1495
7 104,6 4,673251 107,0451
8 95,5 4,623075 101,8066
9 99,2 4,559498 95,5355
10 112,9 4,566595 96,21591
11 109,5 4,55339 94,95374
12 107 4,519327 91,77381
13 104,9 4,500169 90,03235

15
14 103,8 4,464213 86,85267
15 102 4,543031 93,97518
16 100 4,512414 91,14161
Ft merupakan hasil peramalan, yang didapat dengan rumus 𝑒𝑥𝑝𝑜𝑛𝑒𝑛 masing-
masing nilai Forecatsnya. Terlihat bahwa akan terjadi naik turun terhadap Price of
Furniture and Lighting. Dan nilai Peramalannya tidak berbeda jauh dari nilai asli,
maka model yang digunakan memang baik.

Retail sale Time Series

Recommandé

Recommandé

Contenu connexe

En vedette

En vedette (9)

Retail sale Time Series