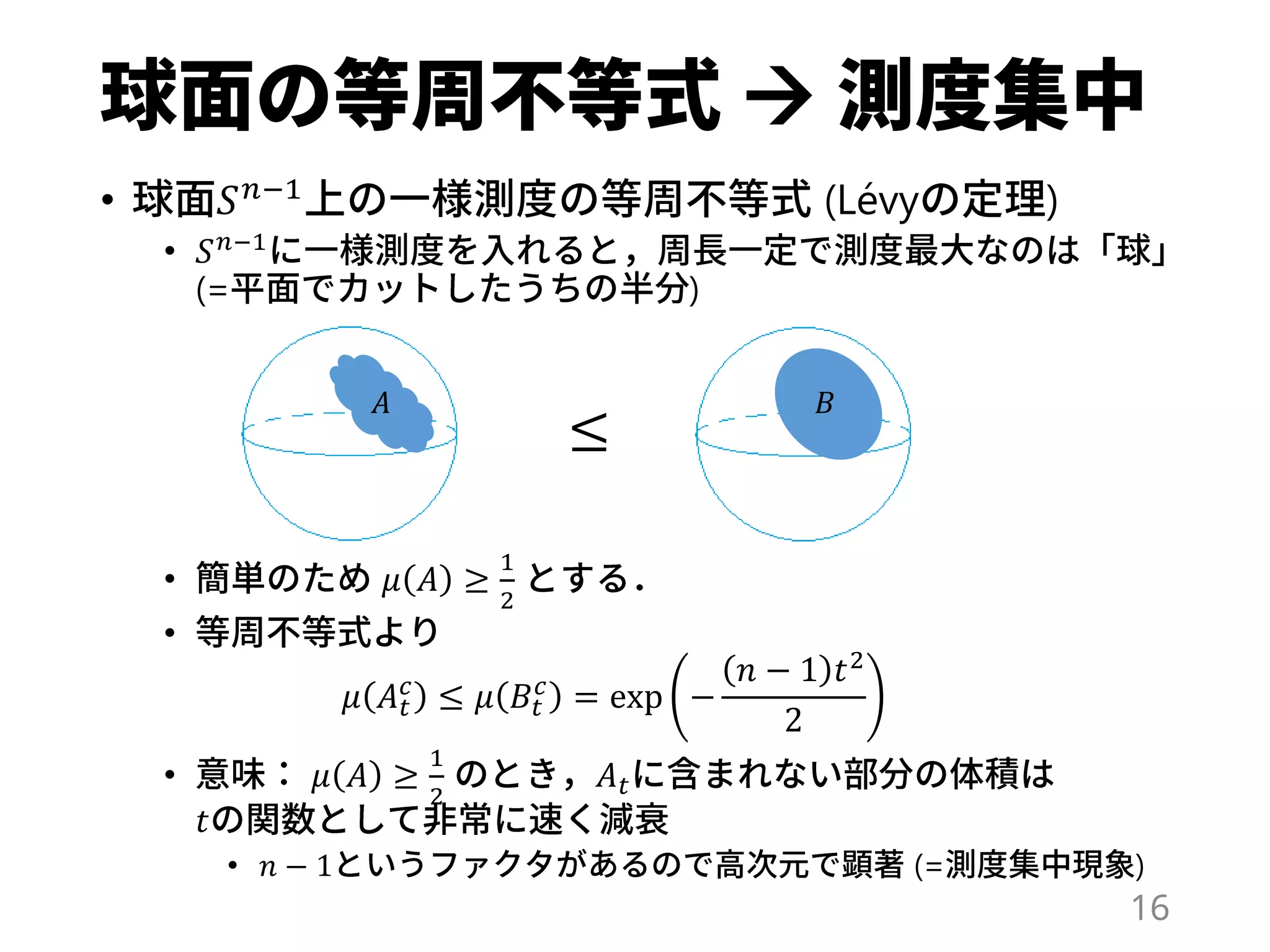
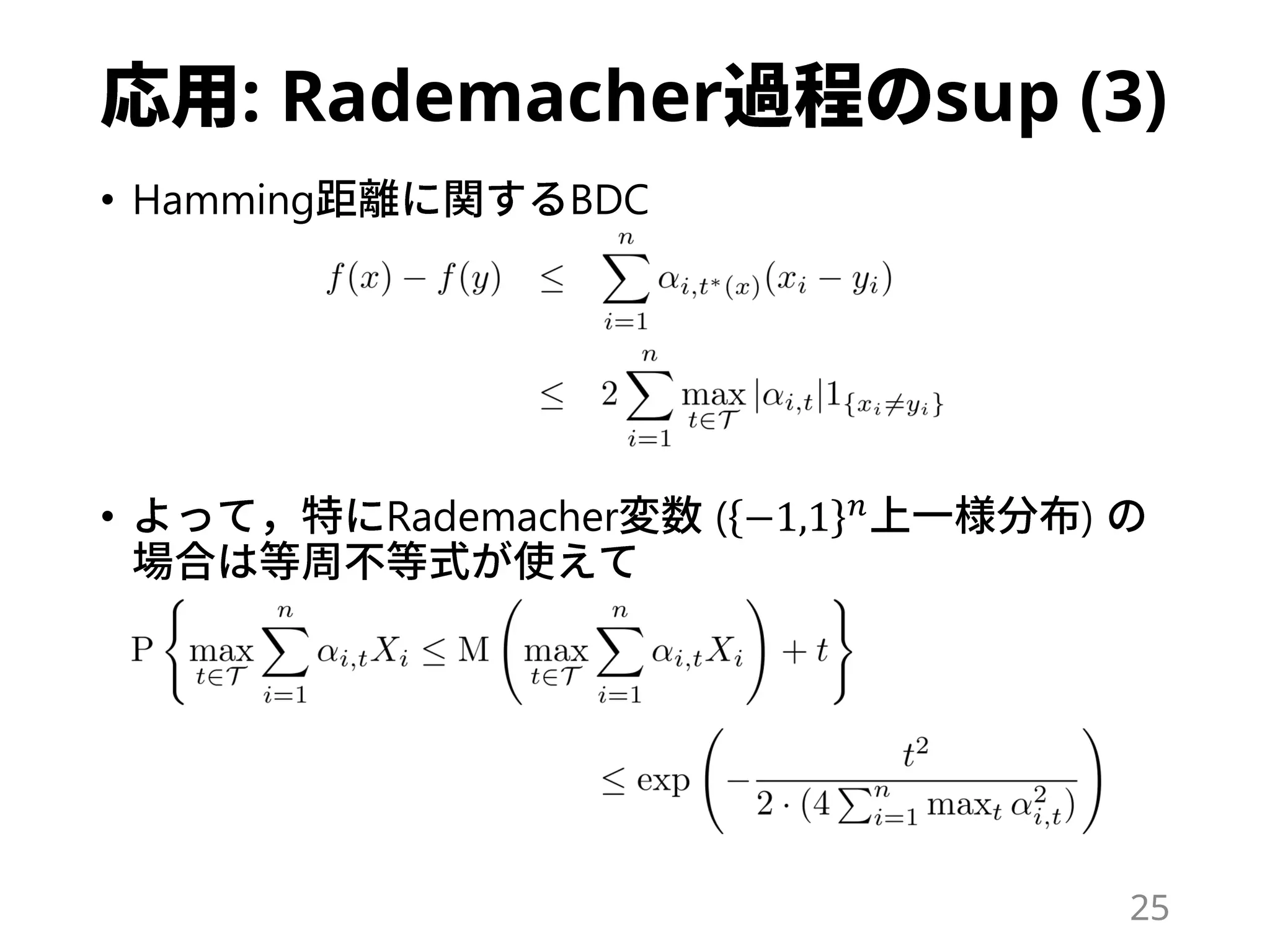
Ce document traite des inégalités de concentration et de la théorie de l'indépendance, en se référant à des résultats et des méthodes statistiques fondamentales telles que les bornes de Chernoff et Hoeffding. Il explore également des concepts avancés et des techniques relatives aux inégalités de distance bornée dans le cadre de l'analyse statistique. Diverses références bibliographiques sont citées, illustrant les applications des inégalités de concentration dans des contextes variés.

1. (ver.1.0)
M1
2015/1/29
1

2. • Q.
• A.
• ( )
• Markov
• Chebyshev
•
• Chernoff bound / Hoeffding / Azuma / Bernstein, etc…
2

3. • S. Boucheron, G. Lugosi and P. Massart:
Concentration Inequalities: A Nonasymptotic Theory of
Independence.
Oxford Univ. Pr., 2013.
• / /
• “theory of independence”
• (cf: Talagrand (1996))
3

4. 1. Introduction ( )
2. – 9. &
• Chernoff bound / Hoeffding / Bernstein
• (Efron-Stein / Poincaré)
• (Han / Pinsker / Ent. / Birge)
• Sobolev
•
•
•
10. – 15. advanced (?)
• 11. – 13. sup
4

5. 5

6. •
• (concentration inequality)
•
• / / / /
/ / / etc…
• Twitter bio
• Talagrand (1995)
•
Chernoff
• Q. (smoothness condition)
6

7. : 1
• 1.1
• 1.2
• 1.3
• 1.4
7

8. • 𝑋1, … , 𝑋 𝑛
• 2 ( )
• =
• =
• Markov
8

9. Hoeffding
• 𝑌: [𝑎, 𝑏]
 𝑉𝑎𝑟 𝑌 ≤
𝑏−𝑎 2
4
• “exponential change” ( lem2.2)
 𝜓 𝑌−𝐸𝑌 𝜆 ≤
𝜆2 𝑏−𝑎 2
8
• Hoeffding
• 𝑋1, … , 𝑋 𝑛 : [𝑎𝑖, 𝑏𝑖]
• 𝑍 = 𝑖 𝑋𝑖
𝜓 𝑍−𝐸𝑍 𝜆 =
𝑖
𝜓 𝑋 𝑖−𝐸𝑋 𝑖
(𝜆) ≤
𝜆2 𝑣
2
• where 𝑣 ≔ 𝑖
𝑏 𝑖−𝑎 𝑖
2
4
= cumulant
 𝑍 sub-Gaussian
9

10. (BDC)
• smoothness condition
• (bdd. difference condition)
• 𝑥𝑖
• Hamming 𝑑 𝑐 𝑥, 𝑦 = 𝑖 𝑐𝑖1 𝑥 𝑖≠𝑦 𝑖
1-Lipschitz
• : BDC
10

11. • 𝑓: BDC
• 𝑍 = 𝑓(𝑋1, … , 𝑋 𝑛)
• 𝑍
• Δ𝑖 ≔ 𝐸 𝑍 𝑋1, … , 𝑋𝑖 − 𝐸[𝑍|𝑋1, … 𝑋𝑖−1 ]
• 𝑍 − 𝐸𝑍 = 𝑖 Δ𝑖
• BDC ⇔ Δ𝑖 𝑐𝑖
• Hoeffding ineq.
𝜓 𝑍−𝐸𝑍 𝜆 ≤
𝜆2
2
⋅
1
4
𝑐𝑖
2
• bounded distance inequality / McDiarmid
11

12. McDiarmid: (1)
sup sup
•
• 0 < 𝛿 < 1
•
• 𝑃: (※ )
• 𝑃𝑛: ( 𝑃 i.i.d.
• P E
• 
12

13. McDiarmid: (1)
•
• BDC
• McDiamid
• ( )= 𝛿
13

14. : 1
• 1.1
• 1.2
• 1.3
• 1.4
14

15. • (isoperimetry)
•
• 𝑛- (Lebesgue 𝜆)
• 𝐴 ⊂ ℝ 𝑛
: ( )
• 𝐴 𝑡 ≔ {𝑥 ∈ ℝ 𝑛 ; 𝑑 𝑥, 𝐴 < 𝑡} 𝐴 𝑡-blowup ( )
• 𝐴 𝑛- 𝐵
𝐴
𝑡
∀𝑡 > 0, 𝜆 𝐴 𝑡 ≥ 𝜆(𝐵𝑡)
15

16. 
• 𝑆 𝑛−1 (Lévy )
• 𝑆 𝑛−1
(= )
• 𝜇 𝐴 ≥
1
2
•
𝜇 𝐴 𝑡
𝑐
≤ 𝜇 𝐵𝑡
𝑐
= exp −
𝑛 − 1 𝑡2
2
• 𝜇 𝐴 ≥
1
2
𝐴 𝑡
𝑡
• 𝑛 − 1 (= )
≤
𝐴 𝐵
16

17. Lipschitz (1)
•
Lipschitz median
•
•
• 1-Lipshitz w.r.t. 𝑑
• ( )
( )
• : median
17
𝑀𝑓(𝑋)
1
2
1
2

18. Lipschitz (2)
• 𝐴 𝑑 𝑡
• 𝐴
• 𝑥 ∈ 𝐴 𝑡 𝑓 𝑥 < 𝑀𝑓 𝑋 + 𝑡
• 𝑑 𝑥, 𝑦 < 𝑡 𝑦 ∈ 𝐴
𝑓 1-Lipshitz
𝑓 𝑥 − 𝑀𝑓 𝑋 ≤ 𝑓 𝑥 − 𝑓 𝑦 ≤ 𝑑 𝑥, 𝑦 < 𝑡
18

19. Lipschitz (3)
•
• median 𝐴 ≥
1
2
• ( )
•
• 𝛼(𝑡) median
• 𝑆 𝑛−1
: sup
•  Lipshitz
19
( )

20. Gauss
• Gauss (Gauss 𝛾 )
• Borell (1975), Tsirelson, Ibragimov & Sudakov (1976)
• ( Sec10.4)
• Gauss 𝐻 extremal set
•  ( ) 𝛼(𝑡) explicit
• 𝑃 𝐴 ≥
1
2
20
 (GP)

21. (1)
• ( )
•
• Hamming
• 𝛼 = (𝛼1, … , 𝛼 𝑛)
• 𝑑 𝛼 Lipshitz = BDC
• 𝑑 𝛼(𝑥, 𝐴) McDiarmid ( Sec. 7.4)
21

22. (2)
• Hamming ( )
• 𝑑 𝛼 1-Lipshitz 𝑓
22

23. : Rademacher sup (1)
• Rademacher complexity
• 𝜎𝑖 1/2 ±1 (Rademacher )
• 𝑅 𝑛 Rademacher
sup
23

24. : Rademacher sup (2)
•
• :
• (i.e. Rademacher )
•
•
• 𝑥 {𝑎𝑖,𝑡}
𝑥
24

25. : Rademacher sup (3)
• Hamming BDC
• Rademacher ( −1,1 𝑛 )
25

26. Talagrand (1)
• Hamming ( )
• Talagrand (Sec. 7.4)
•
• 𝑃 𝑋 ∈ 𝐴 ≥
1
2
𝑣 > 0
26

27. Talagrand (2)
• Rademacher BDC ( )
• =Lipshitz w.r.t Hamming
•
27
𝑥

28. Talagrand (3)
•
•
• 𝑣 = sup 𝑥 𝛼 𝑥 2
2
• Talagrand
28
※ 𝑥

29. : 1
• 1.1
• 1.2
• 1.3
• 1.4
29

30. Efron-Stein
• 𝑋 = (𝑋1, … , 𝑋 𝑛)
• 𝑋(𝑖)
= (𝑋1, … , 𝑋𝑖−1, 𝑋𝑖+1, … , 𝑋 𝑛)
• Efron-Stein (Sec. 3.1)
• [Efron & Stein 1981] 𝑓
• [Steele 1986] 𝑓
• ( : r.v. + Jensen)
30

31. Φ-entropy
• Φ Φ-entropy
• Φ-entropy
(Chap. 14)
• 1 Φ 𝑥 = 𝑥2
 Efron-Stein!
• 2 Φ 𝑥 = 𝑥 log 𝑥
31

32. Sobolev
• ≤
Sobolev
• Gaussian log-Sobolev (Chap. 5)
• : Gauss Sobolev
• log-Sobolev (Chap. 6)
• Gaussian Sobolev
• Gaussian vector
•
32

33. Sobolev  (1)
Herbst
• Sobolev
• log-Sobolev: ≤ *
• 𝑓: ℝ 𝑛
→ ℝ 1-Lipshitz
• ∇𝑓(𝑋) ≤ 1
• 𝑔 𝑥 = exp
𝜆𝑓 𝑥
2
(𝜆 > 0)
33
≤ 1

34. Sobolev  (2)
• 𝑔(𝑥) Sobolev
• 𝑓 𝑋 − 𝐸𝑓(𝑋)
34
(log-Sobolev)

35. Sobolev  (3)
•
•
•
35
( log-Sobolev)

36. median vs.
• Gauss Lipshitz
•
 median
• ( Sobolev)

36

37. : 1
• 1.1
• 1.2
• 1.3
• 1.4
37

38. (1)
※ )
• 𝑃, 𝑄:
• 𝑃 𝑄 𝜋
𝑃 𝑄
•
• (Wasserstein )
38

39. (2)
( )
•
• 𝑋~𝑃 𝑇 𝑌 = 𝑇(𝑋) 𝑄
𝑇
• 𝑥 y = 𝑇(𝑥) 𝑐(𝑥, 𝑇 𝑥 )
• 𝑐 𝑥, 𝑦 = 𝑑(𝑥, 𝑦) ( )
• ≒ 𝑇
• 𝑇
• : 1 2
• 
well-defined
• [Villani08, Chap. 4]
39

40. Talagrand
• KL-divergence 𝐷(𝑄||𝑃)
• 𝑄 𝑃
( ∞)
• Talagrand [Talagrand (1996d)]
• 𝑃 Gauss 𝑄 𝑃
40

41.  (1)
• 𝑓: ℝ 𝑛 → ℝ 1-Lipshitz w.r.t. Euclid
• 𝑍 = 𝑓(𝑋)
• 𝑋~𝑃 (Gauss )
• Jensen coupling 𝜋
•
41

42.  (2)
• (Sec. 4.9)
• ( : 𝜆𝑎 − 𝑎2 = 𝜆𝑎 − 𝑎2 −
𝜆
2
2
+
𝜆
2
2
= − 𝑎 +
𝜆
2
2
+
𝜆
2
2
)
•
• ※ log-Sobolev
42

43. v.s.
• Marton (1996a, b)
•  McDiamid,
• v.s.
•
•
• sup
• (𝑃 𝑍 < 𝐸𝑍 − 𝑡 )
•
• sup
43

44. • /
• P. Massart: Concentration Inequalities and Model Selection. Springer,
2003.
• M. Ledoux: The Concentration of Measure Phenomenon. AMS, 2001.
• :
(pdf)
• M. Ledoux
• Concentration of measure and logarithmic Sobolev inequalities
http://www.math.duke.edu/~rtd/CPSS2007/Berlin.pdf
• Isoperimetry and Gaussian analysis
http://www.math.univ-toulouse.fr/~ledoux/Flour.pdf
• G. Lugosi
• Concentration-of-measure inequalities (@MLSS03/05)
http://www.econ.upf.edu/~lugosi/anu.pdf
• S. Boucheron
• Concentration inequalities with machine learning applications ( )
www.proba.jussieu.fr/pageperso/boucheron/SLIDES/tuebingen.pdf
44