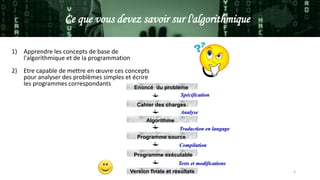
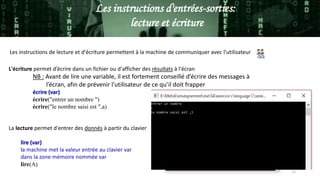
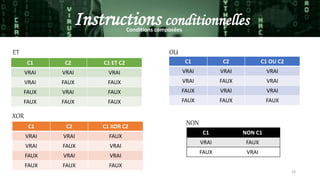
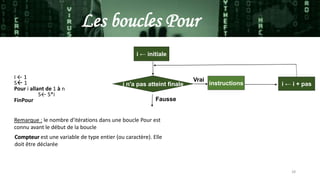
Ce document traite des concepts fondamentaux de l'algorithmique et de la programmation, y compris la définition d'un algorithme, les notions de variables et d'instructions d'affectation. Il explique également les différents types d'instructions, telles que les opérateurs, les boucles, les conditions et les tableaux, ainsi que des exemples pratiques d'algorithmes. L'objectif est de fournir une base solide pour analyser des problèmes simples et écrire des programmes correspondants.

1. 1
Algorithmique
Département de Mathématiques et
d’Informatique
Presented by: Mehdi Abid

2. Le terme algorithme vient du nom du mathématicien arabe
Al-Khawarizmi (820 après J.C.)
Un algorithme est une description complète et détaillée des actions à
effectuer et de leur séquencement pour arriver à un résultat donné.
Algorithme = suite d’actions que devra effectuer un automate pour arriver à partir
d’un état initial, en un temps fini, à un résultat.
2
Définition

3. 1) Apprendre les concepts de base de
l'algorithmique et de la programmation
2) Etre capable de mettre en œuvre ces concepts
pour analyser des problèmes simples et écrire
les programmes correspondants
Ce que vous devez savoir sur l'algorithmique
Enoncé du problème
Cahier des charges
Algorithme
Programme source
Programme exécutable
Version finale et résultats 3
Spécification
Analyse
Traduction en langage
Compilation
Tests et modifications

4. 4
Notion de variable
3+4=
3+4 = 7
Problème : Effectuer le calcule de 3+4
Chez un humain Chez une Machine
(Téléphone – Ordinateur – calculatrice…)
A ← 3
B ← 4
C ← A+B
on stocke la valeur 3 dans une variable A
Et 4 dans une variable B
On affiche la valeur de la variable C
???7

5. 5
Notion de variable
Dans les langages de programmation une variable sert à stocker la valeur d’une donnée
Une variable désigne en fait un emplacement mémoire dont le contenu peut changer au cours d’un
programme (d’où le nom variable)
Règle : Les variables doivent être déclarées avant d’être utilisées, elle doivent être caractérisées par :
• un nom (Identificateur)
• un type (entier, réel, caractère, chaîne de caractères, …)
Identificateur : A,B, Totale ,Prix_TTC, Prix_HT, Test, ch1……..
Type : entier, réel, booléen, chaîne de caractères
Variables A, B, C: Entier
Début
A ← 3
B ← 7
C ← A + B
Fin
Notion de variable

6. 6
L’instruction d’affectation
A ← 3
L’affectation consiste à attribuer une valeur à une variable
(ça consiste en fait à remplir où à modifier le contenu d'une zone mémoire)
En pseudo-code, l'affectation se note avec le signe ←
Var← e: attribue la valeur de e à la variable Var
• e peut être une valeur, une autre variable ou une expression
• Var et e doivent être de même type ou de types compatibles
• l’affectation ne modifie que ce qui est à gauche de la flèche (var)
Ex valides: A ←3 B ←4 C ←A+B
x ←10,5 Test ←FAUX LP ← "ESE"
LF←LP x ←4 x ←C
Question : Quelle est la valeur de x ?
la valeur de LF ?
Affectation

7. 7
Donnez les valeurs des variables A, B et C après exécution des instructions suivantes ?
Variables A, B, C: Entier
Début
A ← 2
B ← 4
A ← B
B ← A+5
C ← A + B
C ← B – A
Fin
Exercice
Instructions A B C
A ← 2
B ← 4
A ← B
B ← A+5
C ← A + B
C ← B – A
2
2
5
44
4 9
94
4 9
4
13

8. 8
Donnez les valeurs des variables A et B après exécution des instructions suivantes ?
Variables A, B : Entier
Début
A ← 1
B ← 2
A ← B
B ← A
Fin
Exercice
Les deux dernières instructions permettent-elles d’échanger les
valeurs de A et B ?
Instructions A B
A ← 1
B ← 2
A ← B
B ← A
1
1 2
2 2
2 2

9. 9
Ecrire un algorithme permettant d’échanger les valeurs de deux
variables A et B
Variables A, B,C : Entier
Début
A ← 1
B ← 2
C ← A
A ← B
B  C
Fin
Exercice

10. 10
Expressions et opérateurs
Les opérateurs dépendent du type de l'opération, ils peuvent être :
des opérateurs arithmétiques: +, -, *, /, % (modulo), ^ (puissance)
des opérateurs logiques: NON, OU, ET
des opérateurs relationnels: ==, , <, >, <=, >=
des opérateurs sur les chaînes: & (concaténation)
Une expression est évaluée de gauche à droite mais en tenant compte de priorités
Priorité des opérateurs
Pour les opérateurs arithmétiques donnés ci-dessus, l'ordre de priorité est le suivant
^ : (puissance)
* , / (multiplication, division)
% (modulo)
+ , - (addition, soustraction) exemple: 2 + 3 * 7 vaut 23
En cas de besoin (ou de doute), on utilise les parenthèses pour indiquer les opérations à effectuer en
priorité exemple: (2 + 3) * 7 vaut 35

11. 11
Les instructions d'entrées-sorties:
lecture et écriture
Les instructions de lecture et d'écriture permettent à la machine de communiquer avec l'utilisateur
L'écriture permet d’écrire dans un fichier ou d'afficher des résultats à l'écran
NB : Avant de lire une variable, il est fortement conseillé d’écrire des messages à
l’écran, afin de prévenir l’utilisateur de ce qu’il doit frapper
écrire (var)
écrire("entrer un nombre ")
écrire("le nombre saisi est ",a)
La lecture permet d'entrer des donnés à partir du clavier
lire (var)
la machine met la valeur entrée au clavier var
dans la zone mémoire nommée var
lire(A)

12. Les instructions d'entrées-sorties:
lecture et écriture
Exemple : Ecrire un algorithme qui demande un nombre entier à l'utilisateur, puis qui calcule et affiche le double de ce nombre
Algorithme Calcul_double
variables A, B : entier
Début
écrire("entrer le nombre ")
lire(A)
B ← 2*A
écrire("le double de est :", B)
écrire("le double de ", A, "est :", B)
Fin
12

13. Algorithme AffichageNomComplet
variables Nom, Prenom, Nom_Complet : chaîne de caractères
Début
écrire("entrez votre nom")
lire(Nom)
écrire("entrez votre prénom")
lire(Prenom)
Nom_Complet ← Nom & Prenom
écrire("Votre nom complet est : ", Nom_Complet)
Fin
Ecrire un algorithme qui vous demande de saisir votre nom puis votre prénom et qui affiche ensuite votre nom complet
Exercice
Exercice
13

14. 14
Ecrire un algorithme permettant de saisir un nombre entier au clavier et d’afficher le carré
d'un nombre saisie par un utilisateur
Variables a, Entier
Début
écrire("entrer un nombre ")
lire(a)
b ← a^2 oubien b a*a
écrire("le carée du nombre saisie est :", b) ou bien écrire("le carré de ", a, "est :", b)
Fin
Exercice

15. 15
Instructions conditionnelles
Les instructions conditionnelles servent à n'exécuter une instruction ou une séquence d'instructions que
si une condition est vérifiée
On utilisera la forme suivante
Si (condition) alors
instruction ou suite d'instructions1
Finsi
Sinon
instruction ou suite d'instructions2
La partie Sinon n'est pas obligatoire,
quand elle n'existe pas et que la condition
est fausse, aucun traitement n'est réalisé

16. 16
Instructions conditionnelles
Exemple : Ecrire un algorithme qui demande de saisir un nombre à l'utilisateur, puis qui calcule et affiche le triple de sa valeur si
le nombre est positif, sinon il affichera son double.
Algorithme Calcul
variables A, R : entier
Début
écrire("entrer le nombre ")
lire(A)
Si (A>=0)
R  3*A
sinon
R  2*A
finsi
Si (A>=0)
R  3*A
écrire("le Résultat est :", R)
sinon
R  2*A
écrire("le Résultat est :", R)
finsi
Fin
écrire("le Résultat est :", R)
Fin

17. 17
Ecrire un algorithme qui demande un nombre entier à l'utilisateur, puis qui teste et affiche s'il est divisible par 3
Algorithme Divsible_par3
Variable n : entier
Début
Ecrire " Entrez un entier : "
Lire (n)
Si (n%3=0) alors
Ecrire (n," est divisible par 3")
Sinon
Ecrire (n," n'est pas divisible par 3")
Finsi
Fin
Instructions conditionnelles

18. 18
Instructions conditionnellesConditions composées
• Une condition composée est une condition formée de plusieurs conditions
simples reliées par des opérateurs logiques:
ET, OU, OU exclusif (XOR) et NON
• Exemples :
• x compris entre 2 et 6 : (x > 2) ET (x < 6)
• n divisible par 3 ou par 2 : (n%3=0) OU (n%2=0)
• deux valeurs et deux seulement sont identiques parmi a, b et c :
(a=b) XOR (a=c) XOR (b=c)
• L'évaluation d'une condition composée se fait selon des règles présentées
généralement dans ce qu'on appelle tables de vérité

19. 19
Instructions conditionnellesConditions composées
C1 C2 C1 ET C2
VRAI VRAI VRAI
VRAI FAUX FAUX
FAUX VRAI FAUX
FAUX FAUX FAUX
C1 C2 C1 OU C2
VRAI VRAI VRAI
VRAI FAUX VRAI
FAUX VRAI VRAI
FAUX FAUX FAUX
C1 C2 C1 XOR C2
VRAI VRAI FAUX
VRAI FAUX VRAI
FAUX VRAI VRAI
FAUX FAUX FAUX
C1 NON C1
VRAI FAUX
FAUX VRAI
ET OU
XOR
NON

20. 20
Instructions conditionnellesTests imbriqués
Les tests peuvent avoir un degré quelconque d'imbrications
Si (condition1) alors
Sinon
Finsi
Si (condition2) alors
instructionsA
Sinon
instructionsB
Finsi
Si (condition3) alors
instructionsC
Finsi

21. 21
Instructions conditionnellesTests imbriqués
Exemple : savoir si un nombre est nul, négatif ou bien positif
Variable n : entier
Début
Ecrire ("entrez un nombre : ")
Lire (n) Si (n < 0) alors
Ecrire ("Ce nombre est négatif")
Finsi
Si (n = 0) alors
Ecrire ("Ce nombre est nul")
Finsi
Si (n > 0) alors
Ecrire ("Ce nombre est positif")
Finsi
Si (n < 0) alors
Ecrire ("Ce nombre est négatif")
Sinon
Si (n = 0) alors
Ecrire ("Ce nombre est nul")
Sinon
Ecrire ("Ce nombre est positif")
Finsi
Finsi
Fin

22. 22
Instructions conditionnelles
Le prix de photocopies dans un centre de copie varie selon le nombre demandé: 0,5 DH la copie pour un nombre de
copies inférieur à 10, 0,4DH pour un nombre compris entre 10 et 20 et 0,3DH au-delà.
Ecrivez un algorithme qui demande à l’utilisateur le nombre de photocopies effectuées, qui calcule et affiche le prix
à payer
Exercice

23. 23
Instructions conditionnelles
Variables Nb_copies : entier
prix : réel
Début
Ecrire (« Saisir le nombre de photocopies : ")
Lire (Nb_copies)
Si (Nb_opies < 10) Alors
prix ← Nb_opies *0.5
Sinon Si (Nb_opies < 20) Alors
prix ← Nb_opies *0.4
Sinon
prix ← Nb_opies *0.3
Finsi
Finsi
Ecrire (“Le prix à payer est : ”, prix)
Fin

24. 24
Instructions itératives: les boucles
• Les boucles servent à répéter l'exécution d'un groupe d'instructions un certain nombre de fois
• On distingue 2 sortes de boucles en langages de programmation :
• Les boucles tant que : on y répète des instructions tant qu'une certaine condition est réalisée
• Les boucles pour ou avec compteur : on y répète des instructions en faisant évoluer un compteur
(variable particulière) entre une valeur initiale et une valeur finale

25. 25
Les boucles Tant que
TantQue (condition)
instructions
FinTantQue
condition instructions
Fausse
Vrai
La condition (dite condition de contrôle de la boucle) est évaluée avant chaque itération
Si la condition est vraie, on exécute instructions (corps de la boucle), puis, on retourne tester la
condition. Si elle est encore vraie, on répète l'exécution, …
Si la condition est fausse, on sort de la boucle et on exécute l'instruction qui est après FinTantQue

26. 26
Les boucles Tant que
Le nombre d'itérations dans une boucle TantQue n'est pas connu au moment d'entrée dans la boucle. Il dépend
de l'évolution de la valeur de condition
Une des instructions du corps de la boucle doit absolument changer la valeur de condition de vrai à faux (après
un certain nombre d'itérations), sinon le programme tourne indéfiniment
 Attention aux boucles infinies
Exemple de boucle infinie :
i ← 2
TantQue (i > 0)
i ← i+1
FinTantQue

27. 27
Les boucles Tant que
Un algorithme qui détermine le premier nombre entier N tel que la somme de 1 à N ( la somme ne doit as
dépassé la valeur 100)
Variables som, i : entier
Debut
i ← 0
som← 0
TantQue (som <=100)
i ← i+1
som ← som+i
FinTantQue
Ecrire (" La valeur cherchée est N= ", i)
Fin
Exercice

28. 28
Les boucles Pour
i n'a pas atteint finale i ← i + pas
Fausse
Vrai
i ← initiale
instructions
Remarque : le nombre d'itérations dans une boucle Pour est
connu avant le début de la boucle
Compteur est une variable de type entier (ou caractère). Elle
doit être déclarée
I ← 1
S 1
Pour i allant de 1 à n
S← S*i
FinPour

29. 29
Les boucles Pour
Calcul de x à la puissance n où x est un réel non nul et n un entier positif
Exercice
Variables x, puiss : réel
n, i : entier
Debut
Ecrire (" Entrez la valeur de x ")
Lire (x)
Ecrire (" Entrez la valeur de n ")
Lire (n)
puiss ← 1
Pour i allant de 1 à n
puiss← puiss*x
( i  i +1 )
FinPour
Ecrire (x, " à la puissance ", n, " est égal à ", puiss)
Fin
=> Pour (i=1,i<=n,i++)

30. 30
Les tableaux
Un tableau est un ensemble d'éléments de même type désignés par un identificateur unique
Une variable entière nommée indice permet d'indiquer la position d'un élément donné au sein du tableau et de
déterminer sa valeur
La déclaration d'un tableau s'effectue en précisant le type de ses éléments et sa dimension (le nombre de ses
éléments)
Exemple
variable tableau A[20] : réel
On peut définir des tableaux de tous types : tableaux d'entiers, de réels, de caractères, de booléens, de chaînes de
caractères, …

31. 31
Les tableaux
L'accès à un élément du tableau se fait au moyen de l'indice. Par exemple, A[i] donne la valeur de l'élément i du
tableau A
Selon les langages, le premier indice du tableau est soit 0, soit 1. Le plus souvent c'est 0 (c'est ce qu'on va adopter
en pseudo-code). Dans ce cas, A[i] désigne l'élément i+1 du tableau A

32. 32
Les tableaux
Saisie
variable i: entier
tableau A[30] : réel
Pour (i=0, i<n, i++)
écrire ("Saisie de l'élément ", i + 1)
lire (T[i] )
FinPour
affichage
Pour (i=0, i<n, i++)
écrire ("T[",i, "] =", T[i]) ou écrire (T[i])
FinPour
ou Pour (i=0, i<=n-1, i++)

33. 33
Les tableaux
Calculer la somme des éléments dans un tableau de taille n
variable i,n,s: entier
tableau A[1…100] : réel
Ecrire (‘entrer le nombre d’éléments du tableau :’) ;
Lire(N)
Pour (i=0, i<n, i++)
écrire ("Saisie de l'élément ", i + 1)
lire (T[i] )
FinPour
s  0
Pour (i=0, i<n, i++)
s=s+ A[I];
FinPour
écrire (« la somme des élement du tableau est ", s)