Les arbres de décision sont des structures de données utilisées pour la classification en divisant les données en sous-groupes plus purs en fonction des attributs. Les algorithmes tels que CART et C5.0 sont utilisés pour construire ces arbres, qui se basent sur le gain d'information pour choisir les attributs à chaque nœud. Toutefois, des défis existent, notamment la gestion des attributs numériques, l'optimisation contre le surapprentissage et la transformation des arbres en règles de classification.

1. FDD et Arbres de Décision
Christelle Scharff
IFI
Juin 2004

2. Généralités

3. 3
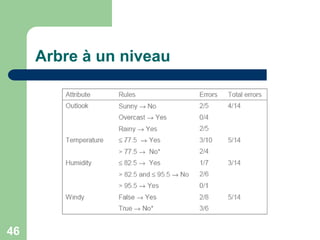
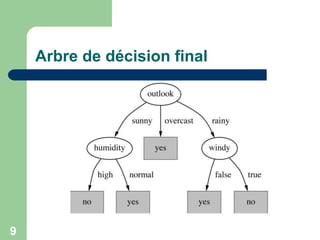
Arbres de décision
 Une structure de données utilisée comme modèle pour la
classification [Quinlan]
 Méthode récursive basée sur diviser-pour-régner pour créer des
sous-groupes (plus) purs (un sous-groupe est pur lorsque tous les
éléments du sous-groupe appartiennent à la même classe)
 Construction du plus petit arbre de décision possible
 Nœud = Test sur un attribut
 Une branche pour chaque valeur d’un attribut
 Les feuilles désignent la classe de l’objet à classer
 Taux d’erreur: La proportion des instances qui n’appartiennent pas
à la classe majoritaire de la branche
 Problèmes: Choix de l’attribut, terminaison

4. 4
Algorithmes
 Les deux algorithmes les plus connus et les plus
utilisés (l'un ou l'autre ou les deux sont présents dans
les environnements de fouille de données) sont CART
(Classification And Regression Trees [BFOS84]) et C5
(version la plus récente après ID3 et C4.5 [Qui93]).
 [BFOS84] L. Breiman, J. H. Friedman, R. A. Olshen,
and C. J. Stone. Classification and regression trees.
Technical report, Wadsworth International, Monterey,
CA, 1984.
 [Qui93] J. R. Quinlan. C4.5: Programs for Machine
Learning. Morgan Kaufmann, San Mateo, CA, 1993.

5. 5
Découpages
IRIS
Les décisions
correspondent à des
découpages des
données en
rectangles

6. 6 I.H. Witten and E. Frank, “Data Mining”, Morgan Kaufmann Pub., 2000.
Météo et match de foot
Attribut but
2 classes: yes et
no
Prédire si un
match de foot va
avoir lieu ou non
Température est
un nominal

7. 7
2 classes: yes et no
Température est un numérique
Météo et match de foot
I.H. Witten and E. Frank, “Data Mining”, Morgan Kaufmann Pub., 2000.

8. 8
Quel attribut faut-il sélectionner?
Classe:
NO
Classe
:YES Classe
: YES

9. 9
Arbre de décision final

10. Arbres de décision et règles de
classification

11. 11
Transformations
 Arbre de décision  Règles (Évident)
– Les arbres de décision représentent une collection
d’implications
 Règles  Arbre de décision (Non évident)
 Optimisations toujours possibles

12. 12
Arbre de décision  Règles
 Attribution d’un prêt suivant la moyenne des soldes
courants (MS), l’age et la possession d’autres comptes
If MS > 5000 then Pret = Yes
If MS <= 5000 and age <= 25 then
Pret = No
If MS <= 5000 and age > 25 and
autres_comptes = Yes then Pret = Yes
If MS <= 5000 and age > 25 and
autres_comptes = No then Pret = No
true
true
false
false
false
true

13. 13
Représentation d’une expression
par un arbre de décision
 Certaines fonctions ne sont pas facilement
représentées par des arbres de décision
 Exemple:
– La fonction paire définie par: le résultat est vrai si le nombre
d’attributs est pair
 Toute formule de la logique propositionnelle peut être
représentée par un arbre de décision
– La logique propositionnelle est construite à partir de:
 Variables propositionnelles
 D’opérateurs logiques: and, or, not,  (implication), 
(équivalence)

14. 14
Règles  Arbre de décision
 Exemple:
if X and Y then A
if X and W and V then B
if Y and V then A
Peuvent être représentées par un arbre de décision.
De plus, Les règles peuvent être combinées en:
if Y and (X or V) then A
if X and W and V then B
Et on obtient un autre arbre de décision de ces 2
règles.

15. 15
Le ou exclusif (XOR)

16. 16
Un arbre de décision pour deux
règles simples
If a and b then x
If c and d then x
Il y a une
duplication d’un
sous-arbre dans
l’arbre

17. 17
Un autre arbre avec duplication

18. Algorithme

19. 19
Pour quels types de données?
 On se restreint d’abord aux données
nominales seulement
 Extension aux numériques:
– Il est possible de traiter les numériques en les
transformant en nominaux (ou ordinaux) par
discrétisation

20. 20
Algorithme
 On considère un nœud
 On sélectionne un attribut pour ce nœud
 On crée une branche pour chaque valeur de
cet attribut
 Pour chaque branche, on regarde la pureté de
la classe obtenue
 On décide si on termine la branche ou non
 Si on ne termine pas le processus est répété

21. 21
Algorithme
algorithm LearnDecisionTree(examples, attributes, default) returns a décision tree
inputs: examples, a set of examples
attributes, a set of attributes
default, default value for goal attribute
if examples is empty then return leaf labeled by default
else if all examples have same value for goal attribute // pure class
then return leaf labeled by value
else
bestatt = ChooseAttribute(attributes, examples) // to be defined
tree = a new décision tree with root test bestatt
for each value vi of bestatt do
examplesi = {éléments of examples with best = vi}
subtree = LearnDecisionTree(examplesi, attributes – bestatt,
MajorityValue(examples))
add a branch to tree with label vi and subtree subtree
return tree
MajorityValue: classe
majoritaire

22. 22
Analyse de l’algorithme
 m : le nombre d’attributs
 n : le nombre d’exemples/instances
 Hypothèse: La hauteur de l’arbre est O(log n)
 A chaque niveau de l’arbre, n instances sont
considérées (best = vi) (pire des cas)
– O(n log n) pour un attribut dans l’arbre complet
 Coût total: O(m n log n) car tous les attributs
sont considérés (pire des cas)

23. 23
Combien d’arbres de décision?
 Considérons m attributs booléens (ne contenant pas le
but)
 Nous pouvons construire un arbre de décision pour
chaque fonction booléenne avec m attributs
 Il y a 2m façons de donner des valeurs aux attributs
 Le nombre de fonctions est le nombre de sous-
ensembles dans un ensemble à m éléments
 Donc, il y a 22m
arbres de décision possibles.
 Comment sélectionner le meilleur?

24. 24
Théorie de l’information
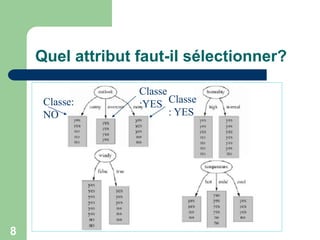
 Besoin d’une méthode pour bien choisir l’attribut
[Shannon & Weaver, 1949]
 Mesure de l’information en bits (pas dans le sens
ordinaire de bit – 0 ou 1)
– L’information peut être un décimal
 A chaque étape,à chaque point de choix dans l’arbre,
on va calculer le gain d’information
– L’attribut avec le plus grand gain d’information est sélectionné
 Méthode ID3 pour la construction de l’arbre de
décision

25. 25
Terminaison
 Tous les attributs ont été considérés
 Il n’est plus possible d’obtenir de gain
d’information
 Les feuilles contiennent un nombre prédéfini
d’éléments majoritaires
 Le maximum de pureté a été atteint
– Toutes les instances sont dans la même
classe
 L’arbre a atteint une hauteur maximum

26. 26 I.H. Witten and E. Frank, “Data Mining”, Morgan Kaufmann Pub., 2000.
Exemple: Météo et match de foot
Attribut but
2 classes: yes et
no
Température est
un nominal
On veut pouvoir
décider/prédire si
un match de foot
va avoir lieu ou
pas suivant la
météo

27. 27
Exercice
 Calculer:
– P(play = “yes”)
– P(play = “no”)
– P(play = “no” | overcast = “sunny”)
– P(play = “yes” | overcast = “sunny”)
– P(overcast = “sunny” and humidity = “high”)

28. 28
Information = Entropie
 
2
2
1
1
2
1 log
log
2
log
1
)
,
( p
p
p
p
p
p
Entropy 


pi est la probabilité de la classe i
pi = # d’occurrences de i / total # d’occurrences
Cette formule est généralisable

29. 29
Entropie pour 3 probabilités
 
))
,
(
)
((
)
,
(
)
,
,
(
log
log
log
2
log
1
)
,
,
(
3
2
3
3
2
2
3
2
3
2
1
3
2
1
3
3
2
2
1
1
3
2
1


























p
p
p
p
p
p
Entropy
p
p
p
p
p
Entropy
p
p
p
Entropy
p
p
p
p
p
p
p
p
p
Entropy
Propriété de l’entropie

30. 30
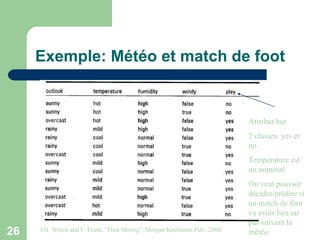
Première étape: Information Outlook
 
bits
Info
Info
Entropy
Info
Entropy
Info
971
.
0
])
3
,
2
([
)
6
.
0
log(
6
.
0
)
4
.
0
log(
4
.
0
2
log
1
])
3
,
2
([
)
6
.
0
,
4
.
0
(
])
3
,
2
([
5
3
,
5
2
])
3
,
2
([












bits
Info
bits
Info
971
.
0
])
2
,
3
([
0
.
0
])
0
,
4
([


Similarly:
Outlook =
“Sunny”
Outlook =
“Overcast”
Outlook =
“Rainy”

31. 31
outlook
yes
yes
no
no
no
yes
yes
yes
yes
yes
yes
yes
no
no
sunny overcast rainy
info([2,3]) info([4,0]) info([3,2])
0.971 0.0 0.971

32. 32
Information pour l’arbre
])
2
,
3
([
14
5
])
0
,
4
([
14
4
])
3
,
2
([
14
5
])
2
,
3
[
],
0
,
4
[
],
3
,
2
([ Info
Info
Info
Info 


La valeur de l’information pour l’arbre après
branchement est la somme pondérée des informations
de l’attribut de branchement.
Le poids est la fraction des instances dans chaque
branche.
Info([2,3],[4,0],[3,2]) = 0.693
Information pour l’arbre complet après le choix de
Outlook:

33. 33
Information sans utiliser l’arbre
bits
Info
Entropy
Info
940
.
0
])
5
,
9
([
14
5
,
14
9
])
5
,
9
([








Outlook

34. 34
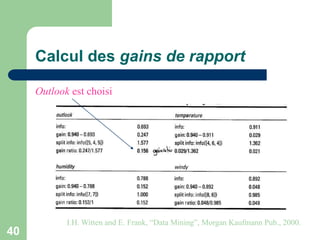
Gain d’information pour Outlook
bits
outlook
gain
outlook
gain
Info
Info
outlook
gain
247
.
0
)
(
693
.
0
940
.
0
)
(
])
2
,
3
[
],
0
,
4
[
],
3
,
2
([
])
5
,
9
([
)
(





De même:
bits
windy
gain
bits
humidity
gain
bits
e
temperatur
gain
048
.
0
)
(
152
.
0
)
(
029
.
0
)
(



Outlook est
choisi

35. 35
Étape suivante
 Sélection d’un deuxième attribut
 On peut examiner:
– Température, Humidity ou Windy pour Outlook =
“sunny”
– Gain(“Température”) = 0.571 bits
– Gain(“Humidity”) = 0.971 bits
– Gain(“Windy”) = 0.020 bits
 Et on continue…
Humidity est choisi

36. 36
Choix du deuxième attribut

37. 37
Arbre de décision final

38. 38
Problèmes lies au calcul du gain
 Les attributs qui ont de nombreuses valeurs possibles
sont privilégiés
– Exemple: Les attributs clés
 Pour corriger ce problème, on utilise une autre mesure
le rapport de gain (gain ratio)
– Calcul de l’information de branchement dans l’arbre en
utilisant:
Original Gain / Information de branchement
– Choisir l’attribut avec le plus grand rapport de gain

39. 39
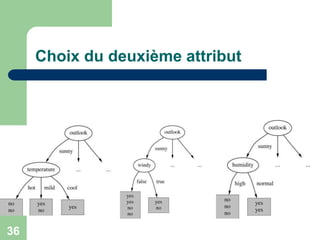
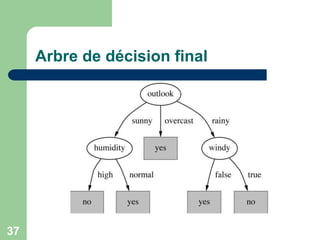
Information de branchement
577
.
1
])
5
,
4
,
5
([
14
5
,
14
4
,
14
5
])
5
,
4
,
5
([








Info
Entropy
Info
Première étape:

40. 40
Calcul des gains de rapport
I.H. Witten and E. Frank, “Data Mining”, Morgan Kaufmann Pub., 2000.
Outlook est choisi

41. 41
Évaluer les arbres de décision
 2 types d’évaluation
– Les performances d’un modèle
– Les performances de la technique de FDD
 Quelle mesure utiliser?
– Taille du modèle
– Nombre d’erreurs

42. 42
Extensions de l’algorithme
 Comment traiter:
– Les attributs numériques
– Les valeurs manquantes
 Comment simplifier le modèle pour éviter les
bruits?
 Comment tolérer les bruits?
 Comment interpréter les arbres de décision?

43. 43
Comment traiter les attributs
numériques?
 Les attributs numériques sont transformés en ordinaux
/ nominaux. Ce processus est appelé discrétisation
 Les valeurs des attributs sont divisées en intervalles
– Les valeurs des attributs sont triées
– Des séparations sont placées pour créer des intervalles /
classes pur/e/s
– On détermine les valeurs des attributs qui impliquent un
changement de classes
 Ce processus est très sensible au bruit
 Le nombre de classes doit être contrôlé
– Solution: On spécifie un nombre minimum d’éléments par
intervalle
– On combine les intervalles qui définissent la même classe

44. 44
Exemple: Les températures
 Étape 1: Tri et création des intervalles
64 | 65 | 68 69 70 | 71 72 | 72 75 75 | 80 | 81 83 | 85
Y | N | Y Y Y | N N | Y Y Y | N | Y Y | N
 Étape 2: Les anomalies sont traitées
64 | 65 | 68 69 70 | 71 72 72 | 75 75 | 80 | 81 83 | 85
Y | N | Y Y Y | N N Y | Y Y | N | Y Y | N
8 intervalles
 Étape 3: Un minimum de 3 éléments (de la même classe) par intervalle
64 65 68 69 70 | 71 72 72 75 75 | 80 81 83 85
Y N Y Y Y | N N Y Y Y | N Y Y N
3 intervalles
 Étape 4: Combiner les intervalles
64 65 68 69 70 71 72 72 75 75 | 80 81 83 85
Y N Y Y Y N N Y Y Y | N Y Y N
2 intervalles
 Étape 5: Changement de classe pour une température de 77.5 ((75 + 80) / 2)

45. 45
Exercice
 Faire de même pour les humidités suivantes:
65 70 70 70 75 80 80 85 86 90 90 91 95 96
Y N Y Y Y Y Y N Y N Y N N Y

46. 46
Arbre à un niveau

47. 47
Les valeurs manquantes
 Ignorer les instances avec des valeurs manquantes
– Solution trop générale, et les valeurs manquantes peuvent ne
pas être importantes
 Ignorer les attributs avec des valeurs manquantes
– Peut-être pas faisable
 Traiter les valeurs manquantes comme des valeurs
spéciales
– Les valeurs manquantes ont un sens particulier
 Estimer les valeurs manquantes
– Donner la valeur de l’attribut la plus répandue à l’attribut
considéré
– Imputation de données en utilisant diverses méthodes
 Exemple : régression.

48. 48
Surapprentissage (Overfitting)
 Adaptation et généralisation du modèle
 Résultats sur l’ensemble d’entraînement et sur
l’ensemble test

49. 49
Simplification de l’arbre de
décision
 Pour lutter contre l’overtiffing on peut simplifier
l’arbre
 Simplification avant
– Simplifier étape par étape pendant la construction
de l’arbre de décision
 Simplification arrière
– Simplification d’un arbre de décision existant

50. 50
Interprétation des arbres de
décision
 Une description adaptée et lisible par tout le
monde
En général, les personnes astigmates doivent avoir
une prescription de lentilles de contacte dures.

51. 51
La méthode
 Apprentissage supervisé
 Le résultat est lisible
– Outils de navigation dans l’arbre
 Les valeurs manquantes peuvent être traitées
 Tous les types d’attributs peuvent être pris en compte
 Elle peut être utilisée comme près traitement
 La classification d’un exemple est très efficace
 Moins efficace pour un nombre important de classes
 Elle n’est pas incrémentale

52. 52
Références
 http://www.grappa.univ-lille3.fr/polys/fouille/
 I. H. Witten, and E. Frank. Data Mining :
Practical Machine Learning Tools and
Techniques with Java Implementations.
Morgan Kaufmann.