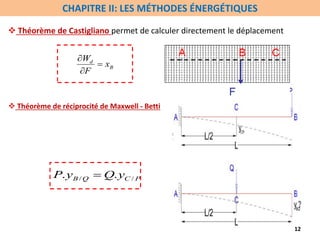
Le cours de résistance des matériaux 2 aborde des concepts avancés tels que la flexion des poutres à l'aide de fonctions de singularités, les méthodes énergétiques et l'instabilité de flambement. Les étudiants doivent maîtriser des théorèmes essentiels comme ceux de Castigliano et Clapeyron, et appliquer ces connaissances à des exercices pratiques. Ce cursus s'appuie sur des bases solides acquises dans le cours de résistance des matériaux 1.

1. Cours de :
Résistance Des Matériaux 2 (R.D.M 2)
Pr Abderrahim BOULANOUAR
2021-2022
Université Abdelmalek Essaadi
Ecole Nationale des Sciences
Appliquées- Al Hoceima
Filière: Génie Civil 1-S2

2. CHAPITRE I: LA FLEXION DES POUTRES EN UTILISANT LES
FONCTIONS DE SINGULARITÉS
CHAPITRE II: LES MÉTHODES ÉNERGÉTIQUES
CHAPITRE III: INSTABILITÉ DE FLAMBEMENT
PLAN
2

3. 3
Cette matière constitue une suite à la Résistance de
matériaux enseignée en premier semestre, on abordera la
flexion des poutres en utilisant les fonctions de singularités,
les méthodes énergétiques et l’ Instabilité de Flambement.

4. 4
Connaissances préalables recommandées
Résistance des matériaux 1, Mathématique

5.  Etudier la flexion en utilisant la méthode de singularité.
 Développer les formules d’énergie de déformation qui
s’appliquent aux cas particuliers étudiés en RDM; la tension et
la flexion.
 Etudier ensuite le théorème de réciprocité, lequel
permettra entre autre d’aborder le théorème de Castigliano.
 Poursuivre l’étude d’une forme d’instabilité, à savoir le
flambement
5
OBJECTIFS

6.  Rappel de la «Méthode de la double intégration».
 Méthode des fonctions de singularités.
 Caractéristiques des fonctions de singularités
 Diagrammes de T et de M par fonctions de singularités
 L’expression de la flèche de la poutre en tout point
6
CHAPITRE I: LA FLEXION DES POUTRES EN UTILISANT LES FONCTIONS
DE SINGULARITÉS

7. La fonction de singularité est définie:
Cette fonction obéit à la loi d'intégration
Pour n 0

Pour n 0
( )
n
n
f x x a
 
0
si x a
si x a
 

 


7
CHAPITRE I: LA FLEXION DES POUTRES EN UTILISANT LES FONCTIONS
DE SINGULARITÉS
1
1
0
1
0
n
x
n
x
n n
x a
y a dy pour n
n
y a dy x a pour n





  

  


 
0
n
x a si x a
si x a
  

 



8. 8

9.  d
dx



( )
q x
.
T q dx
 
.
M T dx
 
2
2
. .
d
E I M
dx


9
Déterminer l'expression de
la pente
On calcul la flèche

10.  Energie de déformation
 Théorèmes pour les structures avec un
comportement élastique linéaire:
 Théorème de Clapeyron
 Théorème de Castigliano
Théorème de réciprocité de Maxwell-Betti
 Principe du travail virtuel
10
CHAPITRE II: LES MÉTHODES ÉNERGÉTIQUES

11. 1 1
.
2 2
ext
W F x C
 
dx
I
M
2
1
dx
I
M
E
2
1
dx
S
T
2
1
dx
S
N
E
2
1
W
0
2
x
z
2
z
2
y
2
d 


 





effort normal + effort tranchant + moment fléchissant + moment de torsion
 Théorème de Clapeyron permet de calculer le travail des forces extérieurs
Energie de déformation totale:
11
CHAPITRE II: LES MÉTHODES ÉNERGÉTIQUES

12. / /
. .
B Q C P
P y Q y

 Théorème de Castigliano permet de calculer directement le déplacement
d
B
W
x
F



12
CHAPITRE II: LES MÉTHODES ÉNERGÉTIQUES
 Théorème de réciprocité de Maxwell - Betti

13.  Définir le flambage
 Equation vérifiée par la flèche
 Elancement, Rayon de giration
 Charge critique de flambage :
 Rotule-rotule soumise à une charge
excentrée
 Flambement d’une colonne avec différents
conditions aux limites
13
CHAPITRE III: INSTABILITÉ DE FLAMBEMENT

14. Le flambement est une sollicitation composée de compression et
de flexion. C’est un phénomène rapidement destructif
 CHARGE CRITIQUE D’EULER L la longueur libre
de flambement
2
2
. .
cr
E I
F
L


I
S
 
L



14
CHAPITRE III: INSTABILITÉ DE FLAMBEMENT
 ÉLANCEMENT
 RAYON DE GIRATION DE LA SECTION

15.  Se familiariser avec le logiciel RDM6 qui permettre de faire comme son
nom l’indique de la Résistance Des Matériaux.
 Bien maitriser les étapes qui mènent à d’étude des différents essais.
 Savoir exploiter les connaissances théoriques acquises du cours RDM1
et RDM2.
TP -1 : TRACTION-COMPRESSION
TP -2 : FLEXION SIMPLE
TP -3 -FLAMBEMENT
15
TRAVAUX PRATIQUES
OBJECTIFS :

16. CHAPITRE I: LA FLEXION DES POUTRES EN UTILISANT LES
FONCTIONS DE SINGULARITÉS
CHAPITRE II: LES MÉTHODES ÉNERGÉTIQUES
CHAPITRE III: INSTABILITÉ DE FLAMBEMENT
16
TRAVAUX DIRIGÉS

17. 17
CHAPITRE I: LA FLEXION DES POUTRES
EN UTILISANT LES FONCTIONS DE
SINGULARITÉS

18. Déterminer:
1. Les actions de contact en A et en D
2. Les efforts tranchants T.
3. Les moments de flexion
4. L’expression de la pente et celle de la flèche.
5. La flèche de la poutre au point C.
On donne la poutre représentée par la figure ci-dessous.
18
Rappel de la «Méthode de double intégration»

19. Les conditions aux limites de la poutre: Le calcul des constantes
 En A : x = 0 et yA = 0
 En B : x = 0 et yB = 0
 En C : x = L / 2 et y’C = 0
(y’ est l'équation de la tangente au
point C)
Poutre reposant sur
deux appuis avec charge
concentrée au milieu
Poutre encastrée supportant une charge
concentrée à une extrémité
 En B :
x = L et yB = 0
x = L et y’B = 0
19