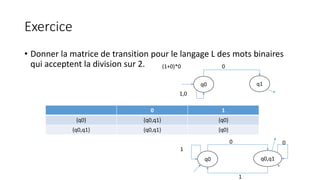
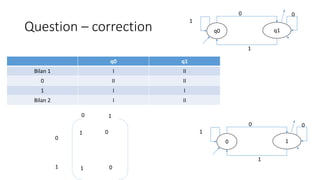
Le document traite de la minimisation des automates finis déterministes et de la construction d'un analyseur lexical pour des langages binaires. Il décrit les étapes pour obtenir des automates minimaux et fournit des exemples d'implémentation avec des matrices de transition. Enfin, il propose des exercices pour créer des automates qui reconnaissent certains mot binaires et la structure de code associée.

1. Explication
1-12-2020

2. Rappel
• La minimisation d’un automate fini déterministe
• La minimisation consiste à retrouver l’automate le plus simple qui
reconnait un langage.
• L’analyse lexicale  la reconnaissance des unités lexicales.
• 1) retrouver l’expression régulière de L sur V.
• 2) A partir du e(L) retrouver l’AFN qui engendre L.
• 3) A partir d’un AFN retrouver un AFDM ( AFDM il faut passer par
ADF)

3. Correction exercice I - AFDM
A B C
Bilan 1 I I II
a I II II
b I I II
Bilan 2 I III II
Le nombre de classe est égale au nombre des états  l’automate est déjà minimal

4. Correction exercice II –
Minimisation
qo q1 q2 q3
Bilan 1 II I II I
a I II I II
b I II I II
Bilan 2 II I II I
Bilan I  Bilan 2 !
II I
a,b
a,b
(a+b)*

5. Matrice de transition
• Retrouver l’analyseur lexical du langage binaire des mots qui commencent
par 1.
• 1) e(L) : 1.(1+0)*
• 2) AFN
• 3) AFDM
• L’automate est déjà minimal
q0 q1
1
1,0
q0 Q1
Bilan 1 I II
1 II II
0 Ensemble vide II
Bilan 2 I II

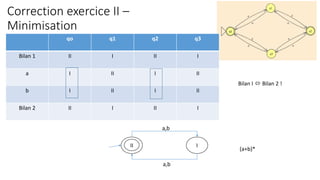
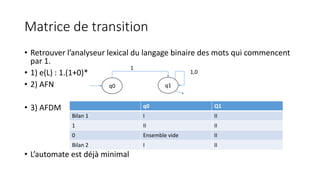
6. Implémentation de l’analyseur lexical
• 4) matrice de transition
q0 q1
1
1,0
0 1
q0
q1
L’état initial
o/ q1
q1 q1
1000
M[q0][1]=q1
M[q1][0]=q1
M[q1][0]=q1
M[q1][0]=q1
Q1 un état final  le
mot est reconnu.

7. Implémentation de l’analyseur lexical
• 4) matrice de transition
0 1
1
1,0
0 1
0
1
L’état initial
-1 1
1 1
1000
M[0][1]=1
M[1][0]=1
M[1][0]=1
M[1][0]=1
1 un état final  le
mot est reconnu.
Toujours l’ensemble vide on le remplace par -1

8. Exercice
• Donner la matrice de transition pour le langage L des mots binaires
qui acceptent la division sur 2. (1+0)*0
q0 q1
0
1,0
0 1
{q0} {q0,q1} {q0}
{q0,q1} {q0,q1} {q0}
q0 q0,q1
0
1
0
1

9. Question – correction q0 q1
0
1
0
1
q0 q1
Bilan 1 I II
0 II II
1 I I
Bilan 2 I II
0 1
0
1
0
1
0 1
1 0
1 0
0
1

10. Structure de code pour l’analyseur lexicale
• 1) fonction de saisie de matrice
• 2) fonction de saisie de mot ( un tableau)
• 3) fonction trace qui permet de retrouver la trace d’un mot
• 4) fonction reconnaissance qui teste est ce que la trace est un état
final ou non.