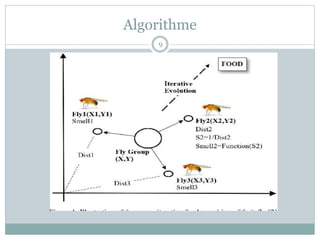
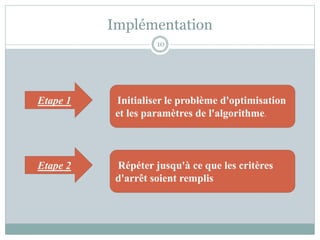
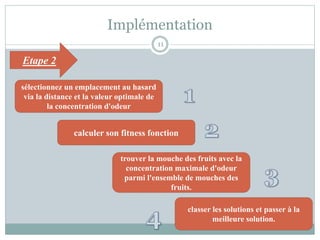
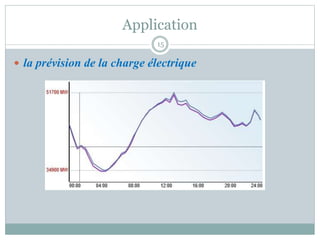
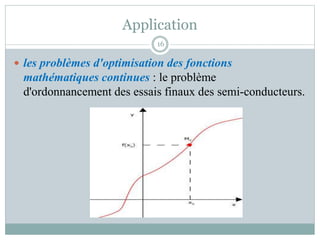
Le document présente l'algorithme d'optimisation des mouches des fruits (FOA), une méthode bio-inspirée développée récemment pour résoudre des problèmes d'optimisation en science et en ingénierie. Il détaille le comportement biologique des mouches des fruits, leur processus de recherche de nourriture et les étapes de l'algorithme FOA, qui incluent l'initialisation, la construction du chemin, le calcul de la fonction de fitness et le mouvement vers l'odeur maximale. L'algorithme est appliqué à divers problèmes d'optimisation, notamment le problème du sac à dos et la prévision de la charge électrique, tout en soulignant sa simplicité et son efficacité.

1. 1
Sujet de l’exposé:

2. Introduction
 Les problèmes d'optimisation sont largement utilisés
en science et en ingénierie . Au cours des dernières
décennies, un certain nombre d'optimisations méta-
heuristiques ont été développées.
 Parmi ces nouvelles méthodes on trouve:
L'algorithme d'optimisation des mouches des
fruits (FOA) , qui est un algorithme bio-inspiré
nouvellement développé.cet algorithme est inspiré
par le comportement de recherche de mouche des
fruits
2

3. Comportement biologique
 Les mouches des fruits
sont de petites mouches
 leurs sens olfactifs
peuvent percevoir des
odeurs extrêmement
faibles de nourriture
flottante dans l'air,
3
En utilisant ces caractéristiques , la
mouche des fruits peut exploiter un
large champ de sources de
nourriture.
Elles peuvent même sentir une
source de nourriture avec
précision jusqu'à 40 kilomètres
de distance
De plus, un seul œil de la
mouche des fruits est composé de
760 yeux unitaires.

4. Processus de recherche
 premièrement, elle vole au hasard à la recherche d'un
endroit avec une odeur particulière .
 Ensuite, l’ échange des informations avec ses
partenaires afin de les comparer et de déterminer
l'emplacement optimal.
 finalement, Après qu'une mouche découvre un
emplacement favorable, elle détermine la forme de
l'emplacement via la dégustation (gout absent ou
piquant).
4

5. Algorithme
 Initialisation : Définir la taille de la population du
groupe de mouches, la condition de fin d'itération et
l’emplacement initial au hasard du centre d’échantillon.
Xi = X_axis + RandomValue ; Yi = Y_axis +
RandomValue
le terme «Random Value » est un vecteur aléatoire qui a
été échantillonné à partir d'une distribution uniforme.
5

6. Algorithme
 - Phase de construction du chemin: la distance et la
valeur de concentration de l'odeur pour chaque mouche
peut être définie via :
Disti= Si =
 Disti est la distance entre le ième individu et
l'emplacement de la nourriture, et Si est la valeur de
decision de concentration d'odeur qui est l'inverse de la
distance.
6

7. Algorithme
 Phase de calcul de la fonction fitness.
Smelli = Function (Si) ; [bestSmell, bestIndex]= max
Smelli ;
Smelli est la concentration d’odeur pour chaque mouche .
Tandis que bestSmell et bestIndex correspondent au
position actuelle de max smell (la valeur de la
concentration maximale d’odeur ).
7

8. Algorithme
 4- Phase de mouvement: la mouche des fruits conserve
la meilleure valeur de concentration et utilisera sa capacite
visuelle pour voler vers cet endroit via :
Smellbest =bestSmell

Remplacer l'emplacement du centre par l'emplacement de
l'odeur maximale.X_axis = X (bestIndex)Y_axis = Y(
bestIndex)
8

9. Algorithme
9

10. Implémentation
10
Etape 1 Initialiser le problème d'optimisation
et les paramètres de l'algorithme.
Etape 2 Répéter jusqu'à ce que les critères
d'arrêt soient remplis

11. Implémentation
11
Etape 2
sélectionnez un emplacement au hasard
via la distance et la valeur optimale de
la concentration d'odeur
calculer son fitness fonction
classer les solutions et passer à la
meilleure solution.
trouver la mouche des fruits avec la
concentration maximale d'odeur
parmi l'ensemble de mouches des
fruits.

12. Implémentation
12
Etape 3
Poster le processus et visualiser ( afficher) les
résultats.

13. Application
 le service logistique des enchères sur Internet
13

14. Application
 l'optimisation du problème multidimensionnel du sac à dos
C’ est un problème d'optimisation combinatoire. Il modélise une
situation analogue au remplissage d'un sac à dos, ne pouvant
supporter plus d'un certain poids, avec tout ou partie d'un
ensemble donné d'objets ayant chacun un poids et une valeur.
14

15. Application
 la prévision de la charge électrique
15

16. Application
 les problèmes d'optimisation des fonctions
mathématiques continues : le problème
d'ordonnancement des essais finaux des semi-conducteurs.
16

17.  De nos jours, un certain nombre d'approches
algorithmiques basées sur le comportement de recherche
de nourriture des animaux ont été développées et
appliquées à divers problèmes d'optimisation
combinatoire.
 Cependant , la FFOA est un nouveau membre. Deux
caractéristiques des mouches à fruits (l'osphrèse et la
vision) sont les éléments constitutifs de la FFOA.
 Les principaux avantages de la FFOA sont la simplicité
du processus de calcul, la facilité de compréhension et
la facilité de mise en œuvre
Conclusion
17

18. 18

19. 19

20. 20

21. 21

22. 22