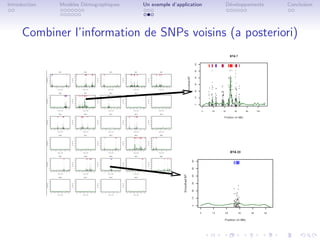
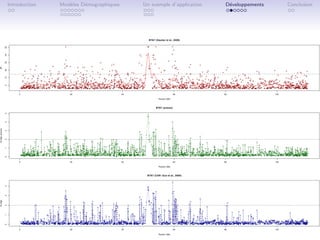
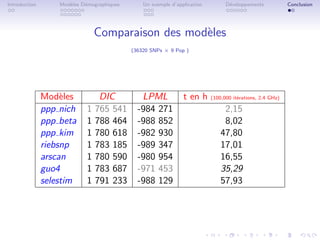
Le document aborde l'utilisation de modèles démographiques et hiérarchiques bayésiens pour étudier la variabilité génétique et la recherche de signatures de sélection à partir de données SNP. Il présente les différents facteurs influençant l'évolution des fréquences alléliques et décrit des méthodes pour modéliser et identifier des loci outliers. Des simulations et comparaisons de modèles sont également discutées, soulignant l'évolution de la différenciation génétique entre populations.

1. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Mod`les hi´rarchiques bay´siens de diff´renciation
e e e e
g´n´tique et recherche de signatures de s´lection
e e e
applications ` des jeux de donn´es SNP haut-d´bit
a e e
Mathieu Gautier
UMR INRA/CIRAD/IRD/SupAgro CBGP
29 Juin 2011

2. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Recherche de signatures de s´lection
e
Forces ´volutives gouvernant l’´volution des fr´quences
e e e
all´liques
e
ˆ Mutation (et recombinaison ` l’´chelle haplotypique)
a e : source de la variabilit´
e
ˆ D´rive g´n´tique : introduit la stochasticit´ (Taille finie des populations)
e e e e
ˆ Migration en terme de flux de g`nes
e
ˆ S´lection
e
Influence diff´rente ` l’´chelle du g´nome
e a e e (Cavalli-Sforza, 1966)
ˆ Facteurs d´mographiques (d´rive, flux de g`ne) ⇒ effet global
e e e
ˆ Selection (mutation et recombinaison) ⇒ effet local

3. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Diff´rentes approches
e
Principe G´n´ral
e e
ˆ D´finition d’un estimateur de la variabilit´ g´n´tique intra/inter
e e e e
population (e.g. FST , EHH)
ˆ Recherche d’outliers (relativement ` l’attendu neutre)
a
ˆ Distribution th´orique (Lewontin et Krakauer, 1973, Bonhomme et al., 2010)
e
ˆ Distribution simul´e (Bowcock et al., 1991, Beaumont & Nichols, 1996)
e
ˆ Distribution empirique (Akey et al., 2002)
Mod`lisation Hi´rarchique (Bay´sienne)
e e e
ˆ Efficace pour distinguer les effets locus des effets population-sp´cifique
e
sur la variabilit´ g´n´tique
e e e
ˆ La distribution (fr´quences all´liques)
e e est connue (ou approchable) pour diff´rents
e
mod`les
e (d´mographiques)
e

4. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
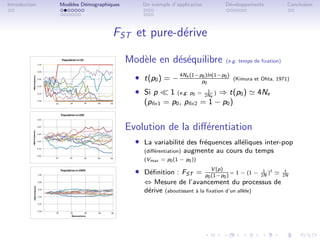
FST et pure-d´rive
e
Mod`le (d´mographique) de Wright/Fisher
e e
ˆ Les populations ont ´volu´ pendant t g´n´rations
e e e e (non chevauchantes) en
complet isolement depuis une population ancestrale commune
ˆ Illustration dans le cas de taille de population constante (N)
Evolution des fr´quences all´liques
e e
ˆ P(Xt+1 = j|Xt = i) = j
2N
ψij (1 − ψi )2N−j
o` ψi =
u i ,E[Xt+1 |Xt = xt ] = xt et V[Xt+1 |Xt = xt ] = 2Nxt (1 − xt )
2N
ˆ E[Xt ] ≡ E[E[Xt |Xt−1 ]] = E[Xt−1 ] = ... = x0 = 2Np0 ⇒ E[pt = Xt
2N
] = p0
ˆ V[pt ] = p0 (1 − p0 )[1 − (1 − 1/2N)t ]

5. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
FST et pure-d´rive
e
Mod`le en d´s´quilibre
e ee (e.g. temps de fixation)
ˆ t(p0 ) = − 4Ne (1−pp0
0 )ln(1−p0 )
(Kimura et Ohta, 1971)
ˆ Si p 1 (e.g. p0 = 2Ne ) ⇒ t(p0 )
1 4Ne
(pfix1 = p0 , pfix2 = 1 − p0 )
Evolution de la diff´rentiation
e
ˆ La variabilit´ des fr´quences all´liques inter-pop
e e e
(diff´rentiation)
e augmente au cours du temps
(Vmax = p0 (1 − p0 ))
ˆ D´finition : FST =
e
V (p)
p0 (1−p0 )
= 1 − (1 − 2N )t
1 t
2N
⇔ Mesure de l’avancement du processus de
d´rive (aboutissant ` la fixation d’un all`le)
e a e

6. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Simulations : 8 pops (2Ne = 500), 10000 SNPs (8500 neu, 250 per s class)
t = 50 generations
t = 100 generations

7. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
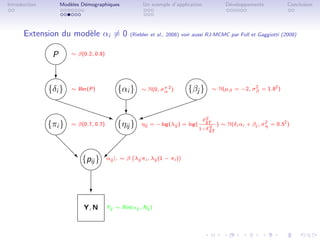
Mod´lisation hi´rarchique
e e
Principe {πi } ∼ β(0.7, 0.7) {cj } ∼ β(1, 1)
ˆ On veut s´parer l’influence de πi
e (p0 ) et cj (d´rive)
e
d
sur la variance des αij
ˆ Contraster les αij inter-pop informe sur les πi
d
d
ˆ Contraster les αij intra-pop informe sur les cj
‚
d ©
{αij } f (αij |πi , cj )
Distribution a priori sur les αij |πi , cj
ˆ αij |πi , cj ∼ N[0,1] πi , cj πi (1 − πi ) (Nicholson et al.,2002)
ˆ 1−c 1−c
c
αij |πi , cj ∼ β πi c j , (1 − πi ) c j
j j
Y, N Yij ∼ Bin(αij , Nij )
ˆ Prior ”exacte” : eq. de diffusion de Kimura (en pr´p.)
e

8. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Comparaisons (4 pops, 300 SNPs, 2Ne=1000)
model 1 (Tr. Gaussian)
1.0
1
2
3
4 4
2
1
3 1
3
4
2
4
3 3
4
1
2 2
1
3
1
4
0.8
2
3
4
2
1
0.6
c value
3
0.4
1
2
4
2
2 4
3
2 3
1
4 1
3
0.2
1
4
2
4
3
2
4 3
1 1
4
1
3
2 t/2N
4
2
1
2
4
1 3 FST=1−(1−1/2N)^t
3
4
2
3
1
0.0
2
3
4
1
10 20 50 100 200 500 1000
Generation
model 2 (Beta)
1.0
0.8
1
2
4 4
3
2
1
1
0.6
2
4 3
3
3
c value
4 4
1
3
1
2 2
1
3
4
2
0.4
3
4
1
2
1
3
2
4
2
4
3
0.2
2
1
3 1
2
3 4
1
4
3
1
2 4
2
3
4 1
4
1
3 t/2N
2
1 2
2
4 4
3 FST=1−(1−1/2N)^t
1
3
2
4
3
1
0.0
2
1
3
4
10 20 50 100 200 500 1000
Generation
model 3 (Exact)
1.0
1
3
2 4
4 2
1
0.8
1
2 3
3
4
3
4
4 1
0.6
3
2 2
1
t/2N
1
3
4
2
0.4
3
4
1
2
1
3
2
4
2
0.2
2
1
3 3
4
1
2
3 4
1
4
3 3
4
2
2
1
4 1
4
1
3
2
1 2
2
4 4
3 t/2N
1
3
2
4
3
1
0.0
4
3
2
1
10 20 50 100 200 500 1000
Generation

9. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Identification de locus outliers : PPP-value (Gautier et al., 2010)
Ecart au mod`le
e (H0 : ´changeabilit´ des loci)
e e
J
[yij −E(yij |πi ,cj )]2
ˆ Mesure de discr´pance : T (yij , πi , cj ) =
e V(yij |πi ,cj )
j=1
πi (1−πi )(1+(nij −1)cj )
avec E(yij | πi , cj ) = πi et V(yij | πi , cj ) = nij
ˆ Pi = P T (yij , πi , cj ) T (yij , πi , cj ) | yij
r
Impl´mentation (MCMC)
e
ˆ A chaque it´ration t, on ´chantillonne yij ∼ Bin(nij , αij )
e e r t

J
Tt (yij , πit , cjt ) − Tt (yij , πit , cjt ) 0
r
ˆ On calcule :

1 si
Pt =
i j=1

0 sinon

N
ˆ Pi = 1
N
Pt
i
t=1

10. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Exemples sur donn´es simul´es
e e (N=10,000 SNPs, 6 pops)
A) T=10 (analysis under model 1) D) T=100 (analysis under model 1)
1.0
1.0
*
0.8
0.8
* *
*
* *
* *
*
* *
*
* *
*
*
*
*
*
*
*
*
* *
*
*
*
0.6
0.6
*
PPPvalue
PPPvalue
*
*
*
0.4
0.4
0.2
0.2
*
*
*
0.0
0.0
0.10 (B) 0.05 (B) 0.02 (B) 0 (N) 0.02 (P) 0.05 (P) 0.10 (P) 0.10 (B) 0.05 (B) 0.02 (B) 0 (N) 0.02 (P) 0.05 (P) 0.10 (P)
SNP selection type SNP selection type
B) T=10 (analysis under model 2) E) T=100 (analysis under model 2)
1.0
1.0
*
*
*
0.8
0.8
*
*
* *
* *
*
*
* *
*
*
*
*
* *
*
*
*
*
0.6
0.6
PPPvalue
PPPvalue
*
*
0.4
0.4
*
*
*
*
0.2
0.2
*
0.0
0.10 (B) 0.05 (B) 0.02 (B) 0 (N) 0.02 (P) 0.05 (P) 0.10 (P) 0.0 0.10 (B) 0.05 (B) 0.02 (B) 0 (N) 0.02 (P) 0.05 (P) 0.10 (P)
SNP selection type SNP selection type
C) T=10 (model 1 VS model 2) F) T=100 (model 1 VS model 2)
1.0
1.0
q
q
q q
q
q q
qq
q
qqq q q
qq
qq qq
q
q q q
q q
q
qq
q q q q
q
qqqq
q q
0.8
0.8
q
q q q
q q qq
q
qq q q
q
qq qq
q qq q q
qq q
q q
qq q
q q qq
q q q q q
qq q qqq
q q q
q q q q qq
qq q
q qq qq
q
q q q
q q q
q q q q qq q q q
qq q
q qq q q
q q qq
q q q q qq q
q qq q q q qq
q
qq q q q qqqq q
q q
q q q q q
q q
qq q
q q q q qq
q q
qq q q q
q q q q q q
q q
q q
qq qq qq q q
q
qq q q
q q q qq q
q
q
q q q q qq q q q q q qqq
q
q q q
q qq q q q q qq qq q
q
q q qq q q
0.6
0.6
q
PPPvalue (model 1)
q qq q
PPPvalue (model 1)
q
qq q
qq
q q q
q qq
q q q qq q q q
q qq
q qq qq
q q q qq q qq qq
qq qq q q q qq q q
qq q
q qq qq q
q q q q qq
qq q q q q
q q qq
q qqq q q q
q
q q q q q qq qqq q qq q qq
q q qq q q q q q
q q q q
qq q q
q q q q q q
q qq q qqq q q
q
q q
q
q q qqq q q q q q
q q q
qq
qq qq q
q qq q
qq q q q q q
q
q q q q qq q q q q q q
q qq q q q q
q
q
q
q q q q q
q q
q q q q q q q
q qqq q q
qq q q q q q
q q q q q q q q qq q q
q q
q q qq q qq q q
q qq q q q q q q q q qq qq
qq
q q q
q q q q q
0.4
0.4
q q q qq q q q
qq q q
q q q q
qqq
q q q qq qq q
qq q
q q
q q q q qq q qq
q
q q q q qq q q q q q q q q qq q q q
q q q q
q qq
q q
q q q q q q qq qq q q q
qq qq
qq q
q q qq
q q q qq q q q q q q q qq
qq q q q qq
q qq q q q q qq q q q q q q qq q
q q qq
q q q q qq
q q qq q
qq q q q
q q qq q
q qq q
q
q q q qq q q q q q q qq q
q
q qqq q q q q
q q q qq qq qq qq q
q q q q q q q q
q q
q qq q
q q q q
q q q q q q qq qq q q
q q qq
qq q q
qq q q q q q q q
q q q
q qq q q q qq q q
q q q
q q qq q q q q
q q q
q q q
q q
q
q
q
q qq
q q q
qq q q
q q q
q
q q qq qq q q
q
q q q
q
qq q
qq
qq q
q
q q qq qqq q
q qq q qq q q q
0.2
0.2
q
q q qq
q q qq q q
q qqqq q q q
q q
q q qq
q qq q
q q qq qq
q q qq q q q
q q q q
q
qq
q q q q qq
q q q q
q
q qq q
q qqq q
q
q qq q
q qqq q
q
qq q qq
q
q
q q
q q q qq q
qqq
q q qq
q
q
q q
qqqq q
q
qq q q q
q q
0.0
0.0
q
0.0 0.2 0.4 0.6 0.8 1.0 0.0 0.2 0.4 0.6 0.8 1.0
PPPvalue (model 2) PPPvalue (model 2)

11. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Le mod`le en ˆ de Wright
e ıle
Migrant pool ( πi )
m1 mJ
mj
Pop 1 Pop J
N1 / pi1 NJ / piJ
Pop j
Nj / pij
A l’´quilibre migration/d´rive
e e i.e. perte d’alleles due ` la d´rive = gain du ` la migration)
a e a
ˆ pij ∼ β λij πi , λij (1 − πi ) ⇒ E(pij ) = πi et V(pij ) =
πi (1−πi )
1+λij
ij
ˆ ij 1
On d´finit FST = 1+λ et λij =
e
ij
1−F
ij
ST
F
ST
ˆ Sous l’hypoth`se neutre (effect locus αi = 0) : λij = λj = 4Nj mj (4xNimmigrants dans la population j)
e
⇔ ´changeabilit´ des SNPs
e e

12. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
S´parer les effets locus et pop sp´cifiques
e e (Beaumont and Balding, 2004)
{αi } ∼ N(0, σα = 1) {βj } ∼ N(µβ = −2, σβ = 1.82 )
2 2
d
‚
d ©
ij
F
{πi } ∼ β(0.7, 0.7) {ηij } ηij = −log (λij ) = log ( 1−F ij ) ∼ N(αi + βj , ση = 0.52 )
ST 2
ST
d
‚
d ©
{pij } αij |. ∼ β λij πi , λij (1 − πi )
c
Y, N Yij ∼ Bin(αij , Nij )

13. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Extension du mod`le αi = 0
e (Riebler et al., 2008) voir aussi RJ-MCMC par Foll et Gaggiotti (2008)
P ∼ β(0.2, 0.8)
c
{δi } ∼ Ber (P) {αi } ∼ N(0, σα 2 ) {βj } ∼ N(µβ = −2, σβ = 1.82 )
2
€€
€€
€€ c
q
€ A
ij
F
{πi } ∼ β(0.7, 0.7) {ηij } ηij = −log (λij ) = log ( 1−F ij ) ∼ N(δi αi + βj , ση = 0.52 )
ST 2
ST
d
d
‚ {p } © |. ∼ β λij πi , λij (1 − πi )
d
αij
ij
c
Y, N Yij ∼ Bin(αij , Nij )

14. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
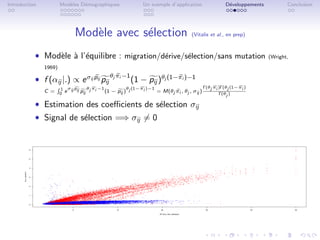
Variable auxiliaire et r`gle de d´cision
e e (Gautier et al., 2009)
P(δi = 1) = E(P)
ˆ δi = 1 ⇒ le SNP est soumis ` s´lection positive (grand FST ) ou balanc´e (petit FST ).
a e ij
e ij
ˆ p(δi = 1) = E(δi ) = EP [E(δi |P)] = P E(δi |P)f (P)dP = P Pf (P)dP = E(P)
0.2
⇒proportion a priori de SNPs sous selection= E(P) = 0.2+1.8
= 0.1
ˆ Le mod`le est robuste ` la prior sur P
e a (see paper)
D´rivation simple d’un Facteur de Bayes
e (Gautier et al., 2009)
ˆ Prior odds= P[δi = 1]/[1 − P(δi = 1)] = 1−E[P]
E[P]
ˆ Posterior odds= P[δi = 1|data]/[1 − P(δi = 1|data)]
ˆ BF peut s’exprimer en unit´ Deciban (BFdB = 10log10 ( Post. odds ))
e Prior
odds

15. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
La r`gle de d´cision de Jeffreys
e e (Good, 1979)
Odds Ratio BF (dB) Strength of evidence
1 to 3.5 0 to 5 ”Barely worth mentionning”
3.5 to 10 5 to 10 ”Substantial”
10 to 30 10 to 15 ”Strong”
30 to 100 15 to 20 ”Very Strong”
100 20 ”Decisive”

16. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Puissance et robustesse
Robustesse
ˆ robuste aux ´carts ` la panmixie
e a (intra-pop) faibles ` mod´r´s
a ee (FIS 0 ou
FIS 0)
ˆ robuste au biais de recrutement des marqueurs
ˆ structure des populations ?
Puissance pour un seuil de 15 dB (”strong evidence”)
ˆ FDR 0
ˆ Bonne puissance pour les SNPs soumis ` une selection positive mod´r´e `
a ee a
forte mais moins efficace pour la s´lection balanc´e
e e
ˆ Si αi = 2 (⇔ s 0.05) : FNR 30%
ˆ Si αi = 3 (⇔ s 0.1) : FNR 10%
ˆ Si αi = −2 (⇔ s 0.1) : FNR 70%

17. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
800 races bovines dans le monde
2 “esp`ces”
e
ˆ Sans bosse : taurins (Bos taurus)
ˆ Avec bosse : z´bus (Bos indicus)
e
Au moins 2 foyers de domestication
ˆ Croissant Fertile (taurins)
ˆ Vall´e de l’Indus (Z´bus)
e e
Migration sur une ´chelle mondiale
e
ˆ Histoire li´e aux flux migratoires humains
e
ˆ Adaptation ` diff´rents environnements
a e
(climatiques, modes d’´levage...)
e

18. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
ACP r´alis´e ` partir d’un jeu de donn´es comprenant 44,706 SNPs g´notyp´s sur
e e a e e e
1021 individus appartenant ` 47 populations diff´rentes (Gautier et al.,2010)
a e

19. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Adaptation des bovins Ouest-Africaines (Gautier et al.,2009)
ˆ ∼ 300 ind. issus de 9 pop ouest-africaines :
5 taurines (trypanotol´rantes),
e 2 Z´bus
e (trypanosensibles) et 2 hybrides ( ?)
ˆ 36,320 SNPs :
MAF0.01 (dans au moins une pop. zebu et une taurine) ⇒∼ 1 SNP tous les 70 kb

20. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
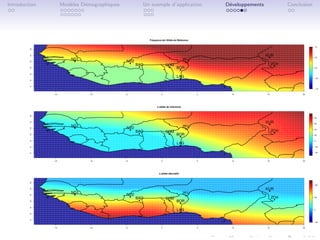
R´sultats
e
P[δi = 1|data] = 0.186

21. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Combiner l’information de SNPs voisins (a posteriori)

22. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Interpr´tation biologique
e
ˆ Au total 53 regions identifi´es
e
ˆ Principales fonctions biologiques impliqu´es
e
ˆ R´ponse immunitaire
e
e.g. MHC region sous s´lection balanc´e
e e
⇒ r´ponse aux pressions li´es aux maladies infectieuses
e e
ˆ Syst`me nerveux :
e
e.g. r´gulation de la temp´rature corporelle, horloge circadienne et reproduction
e e
⇒ nouvelles contraintes environnementales
ˆ propori´t´s des poils et de la peau :
ee
e.g. taille des poils (et des cornes), coloration
⇒ Adaptation ` la chaleur
a

23. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Mod´liser la d´pendance spatiale des SNPs
e e
Un mod`le CAR
e (Guo et al., 2009)
ˆ ij
FST = θij = 1 − (1 − θi )(1 − θj ) et log θi
1−θi
=µ+ i
ˆ CAR prior sur les wij I
i : i | −(i) ∼N , 1
wi+ j wi+ σ 2
o`
u wi+ = wij
i=j j=1
−c3 |dij |
ˆ definition des poids : wij =
c1 + c2 e si j = i
0 si j = i
Limites du mod`le
e
ˆ d´finition des constantes (c1 , c2 et c3 ), contrainte d’identifiabilit´ (
e e i = 0)
ˆ convergence, temps de calcul
Un mod`le autoregressif plus simple
e (en pr´p.)
e
ˆ extension du mod`le BB : π(αi |αi−1 , τα , ψ) ⇒ r´s. pr´liminaires satisfaisants
e e e
ˆ temps de calcul raisonnable

24. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion

25. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Mod`le avec s´lection
e e (Vitalis et al., en prep)
ˆ Mod`le ` l’´quilibre : migration/d´rive/s´lection/sans mutation
e a e e e (Wright,
1969)
ˆ f (αij |.) ∝ e σij pij pij θj πi −1 (1 − pij )θj (1−πi )−1
1 σ p θ π −1 θ (1−πi )−1 Γ(θj πi )Γ(θj (1−πi )
C = 0 e ij ij pij j i (1 − pij ) j = M(θj πi , θj , σij ) Γ(θj )
ˆ Estimation des coefficients de s´lection σij
e
ˆ Signal de s´lection =⇒ σij = 0
e

26. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion

27. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion

28. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Structuration hi´rarchique des populations
e
ˆ Augmentation du taux de faux positifs ` v´rifier avec les
a e
m´thodes Bay´siennes
e e (cf. Excoffier et al.,2009)
ˆ D´finition (a priori) de groupes de pops (sous r´serve qu’ils soient grands)
e e
ˆ Coop et al.(2010) (extension du mod`le de Nicholson et al.,2002)
e
ˆ αij = min(1, max(0, ij )) et i = { ij }j
ˆ i ∼ N (πi , πi (1 − πi )Ω) avec Ω ∼ IW(J, JIJ )

29. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Comparaison des mod`les
e
(36320 SNPs × 9 Pop )
Mod`les
e DIC LPML t en h (100,000 it´rations, 2.4 GHz)
e
ppp nich 1 765 541 -984 271 2,15
ppp beta 1 788 464 -988 852 8,02
ppp kim 1 780 618 -982 930 47,80
riebsnp 1 783 185 -989 347 17,01
arscan 1 780 590 -980 954 16,55
guo4 1 783 687 -971 453 35,29
selestim 1 791 233 -988 129 57,93

30. Introduction Mod`les D´mographiques
e e Un exemple d’application D´veloppements
e Conclusion
Perspectives
ˆ Extension des mod`les pour les donn´es NGS (e.g. Gompert et al., 2011)
e e
ˆ Evaluation (puissance/robustesse) pour diff´rents types de
e
s´lection :
e
ˆ Hard Sweep
ˆ Soft sweep
ˆ Adaptation Polyg´nique
e