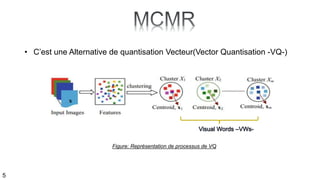
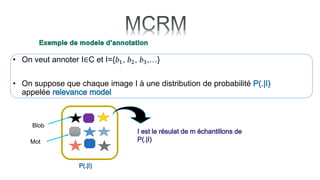
Le document traite de l'annotation d'images, en expliquant différentes méthodologies, y compris la segmentation en régions et l'utilisation de modèles paramétriques pour l'annotation. Il décrit également l'application du k-means pour segmenter des régions d'image et les principes de classification bayésienne et de mélange de gaussiennes. Les étapes de l'entraînement et de l'annotation sont abordées, soulignant l'importance de séparer ces processus.

1. http://www.free-powerpoint-templates-design.com
Free
PPT Templates
Insert the Sub Title of
Your Presentation

2. Introduction
Formulation NB
Annotation des
images avec Word
Co-occurrence
Modèle de Cross
Media Relevance
Annotation des Images
avec les Modèles
Paramétriques
Annotation des
images avec la
Probabiltée
conjointe
Sommaire
Bayesian Classification
Classification avec le
Processus Gaussian
Conclusion

4. • C’est décrire les régions d’une Image
4
Images Ségementation en
Regions
Annotation des regions
Figure: Représentation de processus d’annotation d’une Image

5. • C’est une Alternative de quantisation Vecteur(Vector Quantisation -VQ-)
5
Figure: Représentation de processus de VQ

6. Images Ségementation en Regions Segementation en blobs
• on utilise le K-means pour segmenter chaque Région
• On prend la carte des clusters et chaque cluster est appelé dans la carte
Figure: Représentation de l’alternative de VQ

7. • Soit une collection d’image C non annotées et chaque image I={𝑏1, 𝑏2, 𝑏3,…}
• Soit un ensemble d’entrainement T des images annotées où chaque image J
de T a une representation duel
J={𝑏1, 𝑏2, 𝑏3,…. 𝑏𝑚; 𝑤1 , 𝑤2,…., 𝑤𝑛} 𝑎𝑣𝑒𝑐 𝑤𝑛 : 𝑙𝑒𝑠 𝑚𝑜𝑡𝑠 𝑑𝑒𝑠 𝑟é𝑔𝑖𝑜𝑛𝑠 𝑑′𝑖𝑚𝑎𝑔𝑒

8. • On veut annoter I∈C et I={𝑏1, 𝑏2, 𝑏3,…}
• On suppose que chaque image I à une distribution de probabilité
appelée
Blob
Mot

9. P(w/I)~P(w/ 𝑏1, 𝑏2, 𝑏3, ….𝑏𝑚) =
𝑃(𝑤/ 𝑏1, 𝑏2, 𝑏3, ….𝑏𝑚)
𝑃( 𝑏1, 𝑏2, 𝑏3, ….𝑏𝑚)
𝑃(𝑤/ 𝑏1, 𝑏2, 𝑏3, ….𝑏𝑚) = 𝑗∈𝑇 𝑃 𝐽 ∗ 𝑃(𝑤, 𝑏1, 𝑏2, 𝑏3, ….𝑏𝑚/𝐽)

10. • #(w, J) le nombre de fois de terme w apparait dans l’image J
(generalement c’est 0 ou 1, puisque le même mot et rarement
utilise plusieurs fois dans l’image ).
• #(w, T ) est le nombre totale de fois où w apparait dans les
images d’entrainement de T .
• #(b, J) reflete le nombre de fois certain region d’image est J est
labelisé avec le blob b
• #(b, T ) c’est le nombre d’occurrences de blob b dans T.
• |J| c’est le nombre total des mots et des blobs dans image J,
• |T | la taille de l’ensemble d’entainement.
• Les parametres de lissage αJ et βJ determine le degrée
d’interpolation

12. • on crée un modèle pour chaque image et puis on aggrége tous ses modèles
individuels similaires dans une classe .
• Au lieu de combiné la phase d’entrainement et d’annotation dans le même
processus comme MCMR, les modèles parametric séparent la phase
d’entrainement et d’annotation

14. • L’équation de mélange de modèle de gaussien d’une
caractéristique x de cluster est décrit par
• l :nombre de gaussiene dans le melange
• ∏: le poid de la i-eme gaussienne de melange
• U: la Moyenne de la i-eme gaussiene de melange
• I :covariance de la i-eme gaussienne de melange

16. • Le modèle gaussiene pour chaque classe Ci est definit par l’aggregation
des modeles des images de cette classe
• l :nombre de gaussiene dans le mélange
• ∏: le poid de la k-eme gaussienne de mélange
• U: la Moyenne de la k-eme gaussiene de mélange
• I :covariance de la k-eme gaussienne de mélange