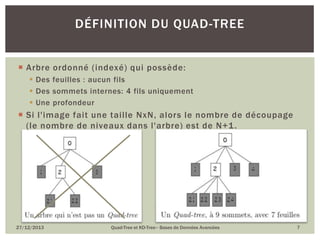
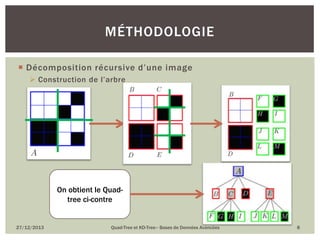
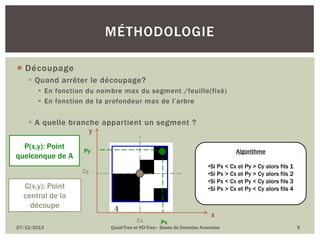
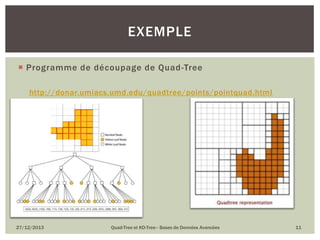
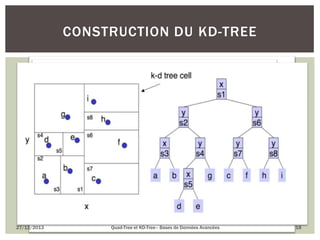
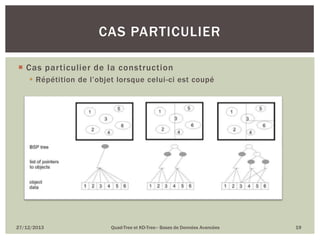
Le document présente le quad-tree et le kd-tree, deux structures de données utilisées pour l'indexation spatiale et la gestion d'objets en deux dimensions. Il décrit leur historique, leur méthodologie de construction, ainsi que leurs avantages et inconvénients. Le quad-tree se concentre sur la décomposition d'images en quadrants, tandis que le kd-tree est une structure binaire pour l'organisation de données dans un espace multidimensionnel.

1. PRÉSENTATION DU
QUAD-TREE ET KD-TREE
Cours de
Bases de
données
Avancées
Aymeric OLIVIER & Patricia MARQUES
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
1

2. SOMMAIRE
 Historique des arbres
 Présentation du Quad-Tree
 Présentation du Kd-Tree
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
2

3. HISTORIQUE DES ARBRES
 Œuvre de beaucoup de recherches :
 Mathématiques et Programmation informatique
 But : trouver un algorithme optimal de segmentation
 Point de vue mathématique :
 James N. Morgan & John A. Sonquist
 1963
 Point de vue informatique :
 J. Quinlan
 1983
 Aucun historique trouvé propres à nos arbres.
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
3

4. LE QUAD-TREE
Source :
https://www.enseignement.polytechnique.fr
http://fr.openclassrooms.com
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
4

5. SOUS-SOMMAIRE
 Principe d’utilisation
 Définition du Quad-Tree
 Méthodologie
 Découpage
 Collision
 Exemple
 Inconvénients de la méthode
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
5

6. PRINCIPE D’UTILISATION
 Méthode d’indexation spatiale
 Gestion d’objet à deux dimensions
 Compression d’objet
 Manipulation d’objet
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
6

7. DÉFINITION DU QUAD-TREE
 Arbre ordonné (indexé) qui possède:
 Des feuilles : aucun fils
 Des sommets internes: 4 fils uniquement
 Une profondeur
 Si l'image fait une taille NxN, alors le nombre de découpage
(le nombre de niveaux dans l'arbre) est de N+1 .
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
7

8. MÉTHODOLOGIE
 Décomposition récursive d’une image
 Construction de l’arbre
On obtient le Quadtree ci-contre
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
8

9. MÉTHODOLOGIE
 Découpage
 Quand arrêter le découpage?
 En fonction du nombre max du segment /feuille(fixé)
 En fonction de la profondeur max de l’arbre
 A quelle branche appartient un segment ?
y
P(x,y): Point
quelconque de A
Py
Algorithme
•Si Px < Cx et Py > Cy alors fils 1
•Si Px > Cx et Py > Cy alors fils 2
•Si Px < Cx et Py < Cy alors fils 3
•Si Px > Cx et Py < Cy alors fils 4
Cy
C(x,y): Point
central de la
découpe
Cx
27/12/2013
Px
x
Quad-Tree et KD-Tree– Bases de Données Avancées
9

10. MÉTHODOLOGIE
 Collision
 Détermination de la trajectoire de chaque segment
 Parcours de l’arbre
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
10

11. EXEMPLE
 Programme de découpage de Quad -Tree
http://donar.umiacs.umd.edu/quadtree/points/pointquad.html
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
11

12. INCONVÉNIENTS
 Notion d’équilibrage de l’arbre
 Zone dense / zone vides
 Exemple de la cabane en plein désert
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
12

13. AUTRES EXEMPLE
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
13

14. K-D-TREE
Source:
http://www.irisa.fr/prive/kadi/DIIC/SDI -2annee/Expose_KdTree.pdf
http://courses.cs.washington.edu/courses/cse373/02au/lect
ures/lecture22l.pdf
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
14

15. SOUS-SOMMAIRE
 Définition du KD-tree
 Cas particulier des BSP -Trees
 Construction du KD-tree
 Cas particulier de construction
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
15

16. DEFINITION DU KD-TREE
 Une méthode de subdivision spatiale
 Un Kd-tree est une structure de données dans un espace à k dimensions
 Un rôle double :
 Organiser l’espace pour accélérer le traitement de données
(Recherche des plus proche voisins)
 Structurer les données sous forme d’un arbre binaire
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
16

17. CAS PARTICULIERS DES BSP TREES
 Cas particulier des BSP trees
 Décompose l’espace en volumes englobants (voxels)
 Découpe chaque voxel en deux sous-voxels grace à un plan
séparateur
 Est réprésenté sous la forme d’un arbre binaire
 Particularité du kd-Tree : plans séparateurs toujours
perpendiculaires aux axes du repère de l’espace
 Simplifie la construction mais aussi le parcours de l’arbre
 Plusieurs possibilités de constructions
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
17

18. CONSTRUCTION DU KD-TREE
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
18

19. CAS PARTICULIER
 Cas particulier de la construction
 Répétition de l’objet lorsque celui-ci est coupé
27/12/2013
Quad-Tree et KD-Tree– Bases de Données Avancées
19