UNMSM - ZAVALA

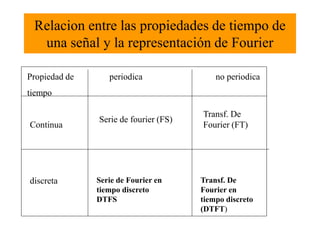
1. Relacion entre las propiedades de tiempo de
una señal y la representación de Fourier
Propiedad de periodica no periodica
tiempo
Continua
Serie de fourier (FS)
Transf. De
Fourier (FT)
discreta Serie de Fourier en
tiempo discreto
DTFS
Transf. De
Fourier en
tiempo discreto
(DTFT)

2. REPRESENTAR UNA SEÑAL PERIÓDICA
MEDIANTE SERIE DE FOURIER
• La figura representa una señal periódica:
)
(
)
( 0
T
t
g
t
g 

G(t)
t
T
Para T0 0
T0 es el valor mas pequeño que satisface la ecuación
t
nf
sen
b
t
nf
a
a
t
g n
k
n
n 0
0
1
0 2
2
cos
)
( 
 

 

Se puede ver facilmente que g(t) es periódica con periodo T0 si se demuestra que:
)
(
)
( 0 t
g
T
t
g 


3. Cont...
• Por lo tanto:Cualquier combinación de senoides de frecuencias 0,
f0, f1, f2, .......,kf0 es una señal periódica con periodo T0.
• Es evidente que si se combinan los valores an y bn es posible
construir una variedad de señales periódicas.
• Determinando los valores de los coeficientes obtenemos:
• Expresando la serie de fourier de manera compacta :


0
0
0
1
0 )
(
T
T dt
t
g
a tdt
n
t
g
a
T
T
n 

0
0
0
0
2
cos
)
(  

0
0
0
0
2
)
(
)
(
T
T
n dt
t
n
sen
t
g
b 
)
cos(
)
( 0
0
1
0 
 

 


t
n
c
c
t
g
n
n
0
0 a
c 
2
2
n
n
n b
a
c 

)
(
1
0 n
n
a
b
tg



4. • Ejemplo

6. Representación de una señal periódica mediante una
serie exponencial
• Dada una señal periódica g(t) se puede representar
mediante:





n
t
jn
ne
G
t
g 0
)
( 
T

 2
0 



T t
jn
T
n dt
e
t
g
G
0
1 0
)
( 

7. Cont........
• Encuentre le serie de Fourier del tren de pulsos rectangular.
• Calculando las constantes:
• Si =T0/5 y A=1 Cn = (1/5)Sinc(n/5).Graficando
T0
A
t
K(t)

)
(
sin 0
0 T
n
T
A
n c
C 



8. Si =T0/5 y A=1 Cn = (1/5)Sinc(n/5).Graficando
-25 -20 -15 -10 -5 0 5 10 15 20 25
-0.05
0
0.05
0.1
0.15
0.2
Cn
no

9. Si =T0/2 y A=1 Cn = (1/2)Sinc(n/2).Graficando
-25 -20 -15 -10 -5 0 5 10 15 20 25
-0.2
-0.1
0
0.1
0.2
0.3
0.4
0.5
Cn
no

10. Si =T0/20 y A=1 Cn = (1/20)Sinc(n/20).
-50 -40 -30 -20 -10 0 10 20 30 40 50
-0.02
-0.01
0
0.01
0.02
0.03
0.04
0.05

11. Si =T0/40 y A=1 Cn = (0.025)Sinc(n/40)
-100 -80 -60 -40 -20 0 20 40 60 80 100
-0.01
-0.005
0
0.005
0.01
0.015
0.02
0.025

12. Cont....
• Ejemplo: verificar la periodicidad de la señal dada por
• Puesto que x(t) tiene discontinuidad en el origen notamos que
las características de la señal no se va ha repetir. Concluimos
que X(t) no es periódica
• SEÑAL PAR E IM PAR
• Una señal x(t) ó x[n] se conoce como señal par ó impar si
se cumple x(-t) = x(t) y x[-n] = x[n] ; x(-t) = -x(t) y x[-n] = -x[n]
repectivamente.
)
cos(
)
(
{
)
( t
t
sen
t
x 
, Si t < 0
, Si t  0
t
X(t) es par
t
X(t)

13. Cont......
• Cualquier señal se puede separar en la suma de 2 señales en la
cual una es par y la otra impar.
|
)
(
|
|
)
(
|
)
( t
x
Od
t
x
Ev
t
x 

|
)
(
)
(
|
|
)
(
)
(
|
)
( 2
1
2
1
t
x
t
x
t
x
t
x
t
x 





0
,...
1
0
,...
0
{
]
[ 

 n
n
n
x
-3 -2 -1 0 1 2 3
. . . . . . . .
. . . . . . . . .
n
1
1/2
-3 -2 -1 0 1 2 3
n
. . . . . . . . ..
. . . . . . .
n
1
0 1 2 3
-3 -2 -1
-1/2
1/2
0
,...
2
/
1
0
,.....
1
0
,...
2
/
1
{
]}
[
{ 


 n
n
n
n
x
Ev
0
,....
2
/
1
0
,......
0
0
,...
2
/
1
{
]}
[
{ 



 n
n
n
n
x
Od

14. Escalamiento en el tiempo
• Sea x(t) una señalen tiempo continuo. El escalamiento en
tiempo continuo den la variable independiente t, por un
factor a se define :
• Si a>1 La señal y(t) es una version comprimida;
• Si 0<a<1, la señal y(t) es una versión expandida.
)
(
)
( at
x
t
y 
-1
0
1
1
-0.5
0
0.5
1
-2
2
0
X(t) Y(t)=X(2t)
Y(t)=x(1/2t)
t
t
t
1

15. En el caso de tiempo discreto
• Escribimos: k>0
• Se define solo para valores enteros de K, si k>1 algunos valores
de la señal en tiempo discreto de Y[n] se pierden . Ver ejemplo
para k=2.
]
[
]
[ kn
x
n
y 
0
1 2 3 4 5 6
-1
-2
-3
-4
-5
-6
n
X[n]
0 1 2
3
n
-3
-2
-1
Y[n]=X[2n]

16. Corrimiento en el tiempo
• La fig. inferior muestra el corrimiento de x(t) a
x(t-2).
• En el caso de una señal en tiempo discreto x[n]
definimos la versión desplazada en el tiempo.
• y[n]=x[n-m] , para m: entero.
X(t)
t
-0.5 0.5
1
2
1
1
0
t
Y(t)=x(t-2)
0

17. Regla de precedencia para el desplazamiento y el
escalamiento en el tiempo
• Sea y(t) una señal que se obtiene de x(t) por medio de una
combinación de desplazamiento y escalamiento en el tiempo
como se describe:
• y(t) = x(at-b) .La relación entre y(t) y x(t) cumple la siguiente
condición:
• Y(0) = x(-b) y y(b/a) = x(0).
• Para obtener correctamente y(t) a partir de x(t) las operaciones
de corrimiento y escalamiento deben efectuarse en el orden
correcto.
• En el escalamiento la variable t se reemplaza por at;
• En el corrimiento la variable t se reemplaza por t-b.dando una
señal intermedia v(t). V(t)=x(t-b) y y(t)=v(at)=x(at-b).

18. • Ej. secuencia correcta de operación:
• Secuencia incorrecta de operación:
-1 0 1 0
-1
-2
-3
-4
1
V(t)=X(t+3)
t
0
-1
-2
-3
1
Y(t)=V(2t)
t
X(t)
t
1
X(t)
t
1
0
-1
-2
-3
1
Y(t)
t
X(2t)
-1 0 1
1
t
-0.5 0.5 -3.5 -2.5

19. Señal exponencial compleja
• Considenado la señal imaginaria:
• la cual es una función periódica como se puede verificar
• Como entonces de allí que el
periodo fundamental es
• Si 0=0 ; entonces x(t)=1 la cual es periódica para cualquier
valor de T.
• Una señal relacionada estrechamente con la exponencial
periodica compleja es: la señal senoidal:
t
j
e
t
x 0
)
( 

t
j
T
j
t
j
T
t
j
t
j
e
e
e
e
e 0
0
0
0
0 )
( 






 
1
0

T
j
e  
 2
0 
T
0
2



T
 
)
(
0
0
)
cos( 


 

 t
j
e e
AR
t
A

20. Potencia y energía de una señal exponencial periódica
• Dada: entonces
• Y la potencia promedio
ya que hay un # infinito de periodos conforme t varía de - a + entonces
la energía integrada es .
• Puesto que la potencia promedio de la señal=1 por cada periodo, si se
promedia múltiplos periodos siempre será =1. Es decir.
• Si se considera un conjunto de exponenciales complejas relacionadas
armonicamente, quiere decir que ellos son periódiocas con periodo común T
y para que implica que K=0, 1, 2,...
•
•
t
j
e
t
x 0
)
( 
 0
2
0
|
| 0
T
dt
e
E
T t
j
periodo 
 

1
|
|
0
2
1 0
0

  dt
e
p
T t
j
T
periodo




 

T
T
t
j
T
T dt
e
P 1
|
|
lim 2
2
1 0

1
0

T
j
e  k
T 
 2
0
0 
0
2
0 T

 

21. Continuaciòn Exp. compleja
• Un conjunto de exponenciales complejas relacionadas
armonicamente tienen frecuencias fundamentales que son
todas múltpiles de una sola frecuencia positiva
• Para es una constante mientras que para
cualquier otro valor K, es periòdica con frecuencia
fundamental y periodo fundamental
0

t
jk
k e
t 0
)
( 
  ,.....
2
,
1
,
0 


k
0

k )
(t
k

)
(t
k

0

k
k
T
k
0
0
2




22. Cont.......
• Ejemplo de Conjunto de func. Exponenciales.
• Dibujar la magnitud de la señal
t
j
t
j
e
e
t
x 3
2
)
( 
 )
5
.
0
cos(
2
)
( 5
.
2
t
e
t
x t
j

-15 -10 -5 0 5 10 15
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
)
(
mod t
x

2 
4

23. Señal senoidal discreta
• La señal
• Se relaciona con
  n
j
e
n
x 0


n
jsen
n
e n
j
0
0
cos
0





n
j
j
n
j
j
e
e
A
e
e
A
n
A 0
0
2
2
)
cos( 0





 





24. Señal senoidal
0 1 2 3 4 5 6 7 8 9 10 11
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
)
12
/
2
cos(
]
[ n
n
x 


25. • Dada ]
31
)
2
(
4
cos[
]
[
n
n
x 

-5 0 5 10 15 20 25 30 35
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1

26. Propiedades de periodicidad de exponenciales discretas
• La función continua tiene la propiedad :
• A) conforme aumenta tambien aumenta la velocidad de
oscilación de la señal.
• B) es periódica para cualquier valor de
• C) Señales diferentes para diferentes valores de
• La función exponencial discreta:
• A) vemos que la velocidad que .Es decir
• es idéntica a las señales con frecuencia 02; 04; 06;..
• B) la no tiene un incremento continuo en la velocidad de
oscilación. Conforme 0 aumenta de 0 a  entoces aumenta su
velocidad de oscilación y si se sigue aumentando 0 de  a 2  su
velocidad de oscilación disminuye.
• es la misma
t
j
e 0

0

t
j
e 0
 0

n
j
n
j
n
j
n
j
e
e
e
e 0
0
0 2
)
2
( 







0

n
j
e 0

0


27. -5 0 5 10 15 20 25
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
]
.
0
cos[
]
[ n
n
x  ]
8
/
.
cos[
]
[ n
n
x 
 ]
4
/
.
cos[
]
[ n
n
x 

]
2
/
.
cos[
]
[ n
n
x 
 ]
.
cos[
]
[ n
n
x 

]
8
/
.
.
15
cos[
]
[ n
n
x 

]
2
/
.
.
3
cos[
]
[ n
n
x 

]
4
/
.
.
7
cos[
]
[ n
n
x 
 ]
.
.
2
cos[
]
[ n
n
x 


28. Ejemplos
• Dada la función
]
12
2
cos[
]
[
n
n
x


0 5 10 15 20 25 30
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
-5 0 5 10 15 20 25 30 35
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1

29. Representación en serie de Fourier de señales periódicas discretas
exponenciales complejas relacionadas armonicamente
• Una señal discreta x[n] es periódica con periodo N si
• N: periodo fundamental mas pequeño.
]
[
]
[ N
n
x
n
x 

n
N
j
e )
/
2
( 
n
N
jk
k e
n )
/
2
(
]
[ 
 
]
[
]
[
0 n
n N

  ]
[
]
[ 1
1 n
n N


]
[
]
[ n
n rN
k
k 
 

     
 
 






N
k N
k
n
N
jk
k
n
jk
k
k
N
k
k e
a
e
a
n
a
n
x )
/
2
(
0 


•0 =2/N es la frec. Fundamental.
• es periódica con periodo N. Además,
• para k=0, 1, 2 , 3,.........
•Las exponenciales discretas que difieren en frecuencia por 2
son identicas. Es decir
•En general

30. 0 5 10 15 20 25 30
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
0 5 10 15 20 25 30
-1
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1
)
31
/
8
cos(
]
[ n
n
x 

•

31. Representación en serie de fourier de una señal
periódica discreta
n
N
jk
N
k
ke
a
n
x )
/
2
(
]
[ 


 



N
n
n
N
jk
k e
n
x
N
a )
/
2
(
]
[
1 
Par de la serie discreta de fourier
.ak: Coeficientes espectrales de x[n]
Estos coeficientes especifican una descomposición de x[n] en una
suma de N exponenciales complejas relacionadas armónicamente.
x[n]=a00[n]+a11[n]+.....+aN-1N-1[n]. K varia entre 0 y N-1
.
x[n]=a11[n]+a22[n]+.....+aNN[n]. K varia entre 1 y N

32. ejemplo
• Considere la señal: donde
• Expandiendo la señal se obtiene:
• Se deduce:
• Graficando para N=5
  n
sen
n
x 0

 N
/
2
0 
 
  n
N
j
n
N
j
e
j
e
j
n
x )
/
2
(
)
/
2
(
2
1
2
1 
 


j
a
2
1
1 
j
a
2
1
1 



33. Continuación ejemplo
• Consideremos: suponiendo que M
y N no tuvieran factores comunes.
• De donde determinamos:
• Los coeficientes de fourier para M=3 y N=5 cuya
grafica es
N
M /
2
0 
 
  n
N
jM
n
N
jM
e
j
e
j
n
x )
/
2
(
)
/
2
(
2
1
2
1 
 


j
aM 2
/
1
 j
a M 2
/
1




34. Ejemplo:
*
)
2
4
cos(
)
2
cos(
3
)
2
(
1
]
[








 n
N
n
N
n
N
sen
n
x
j
a
2
1
2
3
1 

1
0 
a
1
0 
a j
a
2
1
2
3
1 

 j
a
2
1
2  j
a
2
1
2 



35. Onda cuadrada periódica
• Dada


 










1
1
1
1
1
1
2
0
)
/
2
(
)
/
2
(
2
0
)
)(
/
2
(
)
/
2
( 1
1
1 N
m
m
N
jk
N
N
jk
N
m
N
m
N
jk
N
N
n
n
N
jk
k e
e
N
e
N
e
N
a 



 
)
/
(
/
)
2
/
1
(
2
1 1
N
k
sen
N
N
k
sen
N
ak

 

.......
2
,
,
0 N
N
k 


N
N
ak
1
2 1 
 ,......
2
,
,
0 N
N
k 


Al evaluar los 2N1+1 términos de una serie geométrica la cual da como resultado
 
n
x
 
n
x

36. Coeficientes de la serie de fourier Onda cuadrada discreta
N=10 2N1+1=5
N=20 2N1+1=5
N=40 2N1+1=5

37. sumas parciales de la ec:
n
N
jk
M
M
k
k e
a
x
)
2
(





 N=9: par
2N1+1=5
No hay fenómeno de GIBBS

38. CONVERGENCIA DE LA SERIE DE FOURIER DE UNA
ONDA CUADRADA CONTINUA-FENOMENO DE GIBBS
• Aproximación de la serie finita




N
N
k
t
jk
k
N e
a
t
x 0
)
( 