MATERIAL DE CÁLCULO

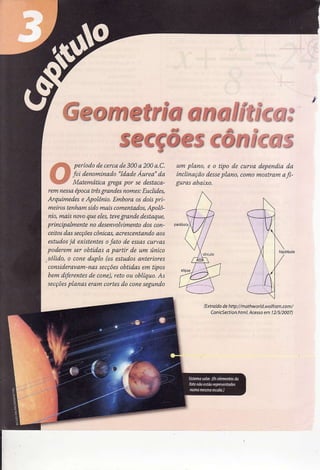
1. Ê
Geonretria
anaÍff$cw*
secçôes eômfems
periododecerca 300a 200/t.C. um plano, e o típo d,ecurvít dependíada
de
foi denomínado Áurea' da
'ld.ad.e ínclinaçâo plano,comomostram
desse af.-
Matemátícagregapor se destaca- gurqsabaíro.
rem nessa época grandes
três xoues:Euclídes,
Arqwmedes Apolònio.Emboraosdorspri-
e
meíros tenham sidomaiscomentados, Apolô-
nío,maísnovoqueeles, gM dedest1que,
teve
príncipalmetate desenvolvimento con-
fio dos
ceítos secções
das cônicas, acrcscertand,oaos
estutlosjá eeístentes fato de essas
o curvas
poderem obtidasa parLir de um üni"o
ser
sólído,o coneduplo (os estadosa teríorcs
consideravam-nas secções obtídas típos
em
beu diferentes cone),
de reto oa ablíqua.As
secçoesplanaseraft cortes cone
do segundo
(Extra|do hftp://nsthwo d.woIíron.can/
de
Conicsectian.htnl.
Acessa 1
en 2/5/2A07)

2. l. A eLipsepodeseÍ€ncontrada partiÍde uÍÍìaexperlênca
a até
divertida. tasvezes étnbalhada ensino
N4u ea no fundarnental:
. FixârÍì-sedos
preqos demade urnâ
nun-ìêtábua íaê digtànclâ
qla quer (porém malor quezero)Lrm outÍo
do do
. Umbarbante, comprlffrento
de maÌor quea dlstánca
do es
é poí
co hidapaíaos pr€gos, amârrado 5ua5 dades
exlreÍn
nesses s pregos.
do
oï . Comum ápls, esÌcamos barbante ÍÍìáx e,fÌncando
o ao mo
suâpontêna rÍìadelra descTevernos lnhâ,
uma dandoLrma
vota lntelra.
. Asslnìfìcará in€ada € lpse mad€lra.
de a na
Observe af gurãa segulr ldentfÌque è ose €mentos za-
e ne uu
oopèèàcor '-doo"-loses-ge'oaâ ^. stoé o èóê_
m€ntos coÍÌespond€riarÍì pregos, inhã ao baÍbante.
aos à €
DasobrasdeApolôníoquenãose
perderam, ma.ís
a import1ntenãoAs
Cônicas, que aperfeiçoou suPerou
e
osestud,os íntefiores Sobre assufito
o
e íntroduzía as denominações elíp- wlklped
EÍa fìguÍa extíaídê rile http://pt
foi do Ìpse
a.org/wlkl/E
se,pará.bola hipérbole.
e Acessando o,vocêpoderá
vê-aernríìov mento.
Especialmente AstronomiLen'
a
a) Denonìine e B os pontos
A quecorrespondem pregos.
aos
cotrou, nas secções cônícas,grande llnindoos € prolongândo segírìento encontTaT
esse até o
aplicação.Copérníco, Kepler,Halley e contoÍno dae1p9e deterrninamos pontos,Chame-os
doÌs de
por
Ne14ton, e,.emplo, f.zeram uso de Re P,Represente M o pontodê ellpse,
com indicaoo v-âr_
erÍì
paro e&plícar -e'o d 9L a.)Lpo do qLeo oâ bd e"eca 0. ea
suasconfgura,ções Íenô- dlstânc entre pregos de 8 cnì,ca
a os seja culeasÍnedjdasde
menos Íísicos, como as tuajetóríLs dos Aq BP Rqe a sonìa + N,48.
e Alú
pLanetasou a, twjetóríL descrítapor b) O queacontecerá a e ipse apÍox
conì 5e maímos mals mai9
e
um projétíL ospregos do outro?
uÍíì
Ao seremínseridasna Geometria 2. FolKep qÌrem
er deduz queasórbltas panetas
u dos eram lp
e
geo' e como osastrÔnomos o
t cas nãocÌrcL.rlaÍes, acÍeditavam anter
analítíca, def.nidascomo lugares 'e9 _'ì," caoospo'copeír D/-.e.è-berÍo e'.sè d€
co
métrícos (cofijuntos pontosqueverí-
de cobertadeu'p stas'parateorada grêvtação NewÌon
a de Ob
rt.am uma.certqpropriedade),as sec- encontre os e ementos
servandoóíbitae lptcaa seguiÍ,
a nelè
côfiícas haram am6.expressão
ga que
daelpsse vocé constrLriu.
ções
algebrica,ampLíando ttítda maís sua
ímportânciae suaaplicabílídade.
Neste capítulovamos partír dasde'
fníções desses lugaresgeométrícos para
as equações algébricasqueas reprnefi-
estudarsuaspropríedades íden-e Fiquta *t tail a de http//w /gen.iïiestÒfr /Pa LiI htt/ 536 eca i.ôf htn l.
rc/ rú n
tqm, l.e*aen 1ó/5/2447
tì,f,carseus elementas.Faremos ama ín'
troduúo 6.0assunto considerando ape-
nqs as cônicas que apresentam eitíos
para.lelos eíxoscoordenados,
aos sendo
sua complementação estudada maís l^
t6rde,emcurs6 superíores. x"-L ji-
-Ot ,7

3. Matêmát Contsxro kaçõ".5
o' &Ap
Introducão
Considere seguìntes
as sltuaçóês:
 trajetóriâ umprojétil,em
dê queda
livre, umarco paúbola.
é de
tr
Osplanetas
giËm erntornodo Solnumatr4etória
cujafoÍma umâe/ipse.
é
O gráfìcoque pressão
rêlaciona evolume umgás
de atempeÊtun
constantê,
como dafÌgura, uma
o é áipélbole.
Veja situações quêâparêcemparábola,elipsê a hipérbole:
mahalgumãs em a a e
Parábola
Origem
Vamosconsiderar cone
um circular seccionado umplano
reto por paralelogêtaÍiz,
à comomostrâm
osdese-
nhos
segulntes:
-&--4h-4,
Nessecaso, q
dizemos ue foì obtidâumasecção
côni.a.hamadapaúbola,

4. (aDítulo3 GeoÍìetdaanalítcarse(!Ões!ônkaj
. 7t
DefiniÇão elementos
e
.F consideremos, plâno papel,
Inicialmente no do umaretad e um pontoF que
nãoDêrtenceela.
a
vamos marcar,agora, série pontos êttãoa uma
uma de que
mesma distância pontoíìxado e da retad. NaprátÌca,
do F isso
podeserfeitocomo auxílio umôrégua, esquadro,
de um lápìs,
alfÌnete baÈante,
e
construìndo gráficoponto à pontoteremogl
o
A parábola o conjunto todosos pontos plano
é de do queestão mêsma
à
distância F ed.
de
Nafìguradevemosdestacar: p
.vt= i=FD c
..- Z=
. o pontoF,focodâparábolà;
. Todopontodaparáboh
. a retad, diretrizdapãrábola; t€messa e todo
Éiiopriedad€
pontodo plano possli
que
. o pontoVvértice parábolã
da (ponto deFD,distância F atéd);
médio de pÌopri€dade
€ssâ pertenceà
. â retaquêpassa F,perpendicu à dhetrlz quesechama
por lar d, êixodesimetrìa paráboìa.
dâ parábolâ;
. a medida F--D,
de parâmetro (p)daparábola.
definimos parábolao lugargeométrico pontosdo
Assim, que é dos plano
quedistam
ìgualmente umaretâ
de
fixad,chamadadileütz, deumpontofixo não
e F, pertencêntê
à diretíz,
chamado
foco,
Equaçãoda parábola
(d),
A pôrt;rdo foco(F)e da diretriz podêmos à da formada todosos pontos
chêgar equação parábola por
plano
P(x,y)do talqled(P, F)= d(P,d).

5. 74 Marmátio, &Aptkàçõsr
conrexto
Vamosdeterminar equação parábola tem comodiretriz retade equaçáo : -4 e comofocoo
a da que a x
pontoF(6,2)i
t
Ne5se ponto
caso,oVérticeéo médio segmento noqualF(6;2)
do FD, eD(-4,2)i
(É' -4 )+ )
vl _:______. | =ví] 2)
:__:_:
2 2)
Pêla'dlstância atéF encontramos
deV o valor c:
dê
c=r/(o-t )' + (2 -2 )' 1 = 5
Ospontos da sãotalque F)= d(P, emqueQ(-4,y):
P(x,y) parábola d(P, Q),
d(p, = dtp,
D ol.+ r,{xlÌF-I tíl zf = .,(x+ 4f + (y - + (x- 6),+ (y- 2F= (x+ 4),+
',F
+ (y- 2),= (x+ 4),- (x- 6),= / + 8x+ 16- / + tzx, za= zox zo+ (y- 2)z 20(x .ì)
- : -
Obseruemosquenaêquaçãoobtidaaparecemascoordênôdãsdovérticexv=têyv=2êtambém
(Y- 2)':=20(x 1)
Y"+ V +x"
4,5
v
c
Reciprocamentq da da (y =
a paftìr equaçáo parábolã, - Z1z 2g1t< 1),podemos
- chegar véftice aovalor
ao e
dç c(distância
deVâ F oudêVà diretríz
d)e,dal aofocoe à diretriz:
(y 2)'z 20(x 1)= 4. s(x- 1)
= -
e m q u e V( ].2) e c=5.
Esboçando o gráfìco,
veml
Logo,F(6,2)ê diretrizx= -4.

6. (apílulol. 6e0melanalítkãrç.!ões
a óni.as
Generalizando, podemosdizerque a partirdo íoco e da diretrizé possível
determinar vérticeV(Á,,y,,)e o
o
valorde <e, daí,a equação pôÍábolâ posiçâo
dã ea vêja
correspondêntê, os casos possíveis:
(y-yv)']=4c(x-Ç ( y- vv) ' := 4c( x- )
-
estudamos
Quàndo
sráfìco umâ
d€ fun(ão
:
(x- &)'z 4c(y yJ (x-xv)z= -ac(y - yv) horizonial. quê?
Por
d
.__ q_
lembrâr vale reclprocara dôequação parábola
Devemos quê a partiÍ da podemos
chegar vértice aovalor
âo e
de c e.daLao íocoe à dketriz.
Observação: volumê1 dêstacoleção,
No estudamosasfunçóes quadráti-
casy : ax2+ bx + c, cujosgráficos foram chamados pãrábolâs.
de Nã
verdàdeaquelas parábolas as€studadôs
e nestecapítulosãoas mesmas,
poìsquôndousamos técnicade completar
a quàdradospodemostrans-
formarqualquêr êquâçáo tipo y = ax':+ bx + c, vìstâno volumel, em
do
umado tipo (x - ,)'?: ì4c(y _ y,),comotemostrabalhado nêstevolume.
l. DetêÍm a equação pafábo€ focof(0, -5) e
ne da de Como disiâncjas g|Jâis,
as são temos:
=
diretrizy 5. 0'+ (y - 5)'?
x'z+iy + 51'z= +
Rêsolüçâo: a r' y av ,
-r-í
.) x. = -2Ay
F[0.-5] está exoy y = 5 é paÉlea exox e
no ao
V[0,0].AdistâncadeFaVé
I-. ---.----=
c=vu +t-5J_ =5
Usando diretarnente
a fómua,temos:
ix - 1'z= -4c(y yv)ã
ì [x - o)'z=-4.5(y 0) +x'?= -20y
Logo, equaçãox'z= -20y.
€ é
2. Deler _eo'ocoe à o 'êt1z pãrabola equaçao
r ca oe
Usanao propredade todoponto
a de P[x,y] da páÍé Y' = 5x.
Resolução:
escÍevef = 5xcomo
Pod€rnos y'z
o P. F - J r . o J -f)-5 Y -JJ l y |'t'
iy o r , = 4 . ; s - o
Ad srà1cdePà relry -. ê gJdã disl_cê
é dePaté
A distânc dovénce(0,0l aofocoé c =
a
[x,5], qlreé igualâ{(x - x} + iy - 5Ì

7. Obaêruação:0 vaoÍ do coeÍcÌenÌe ndcaa distân
c
=
Looo, o)eaoretlzex-f
r[9, oa oo Íoco verl.è e , o seqüe1te-ìerre,
ao è concal
dadedapaÉbolâ.VejacomoexemposaspãÍáboasd
fesolvldo emy'z 8x(c = 4),a concâvdâ-
exercício 3: =
deéÍnaoÍque emy'= 4x[c = ]), pois4 l
>
4.Deteminea equâção as coordenadas vénice
e do da
pafábo quetemfocono ponto 5) e a Íetadiretriz
a F(1,
deequaçãoy= 3.
Rê3olução:
0s dados prcberna
do pefrnitern urnesboço
fazeÍ do ï
gráÍìco ass identÍcâr tpo daequação:
e, m, o
3,Esboce gráÍcos parábolâs equâção
os das de
a) y ' 1= x : b)y,=4< cly,=ex.
Rcsolüção:
o y,=x=r. | x
D 0,-ì
tx xv), = aciy - y,l
00, O védceé o ponto rnédio F--D.
de Então:
Lr L Vl-1 .-l :-i l= Vf t tì
2 2 )
! 12
42 Pela é c s oeVa F e_cor'aÌros,€ oec
dis o or
c= i( r D' + ts- ì' = Jo+ 16 = 4
rí*,1
b)y'?=4x=4.]x Podemos escrcver pfocLl€dal
agora equação
a
tx - xv),: 4cty- yv)+ [x 1), = 4. 4(y - 1),-
i I L! + tx - ll'z= l6ty - 1)
oo Logo, equação(x - l), = l6ty - 1l eVtl, ll.
a é
,-|;
5. Seurna pâráboa como
t€Ín equação
4 tl x, - 4x - t2y - 8 = 0, d€terrn ascoofdenaoas
ne oo
-t vértLce, coordenadas foco, eqlação retad-
as do a da
"t rctz dê paÉbola a equação e xode stmet|
e do a
Resolução:
Competando quadÍados
os perfeitos,
temos:
'7-4 l2v-8-o:2 t"- 2y-B-
=
+ x'z- 4x + ..1... l2y + I + ..L.-=
c)
= '?-4x+4 =12y+12à
= lx - 2), = 12(y 1)=, [x - 2)2 4. 3(y+ ]) em
+ =
que=2,yv- I ec=3
-èzê-ao esooço graìco, r:
Ln do ve
Logo, -lJ, F[2,2), d retrz = -4 e o eixo
V(2, a éy de
smet|aéx=2.

8. (apÍtulo3 GeometÍia
. analitka:5eqõe5ón
os tl
6. Deleriìe a eqJaÉo. ofocoFe a o ÍetÍ'z oépê àoo
d Rêsolução:
a comvéftrce que
V(-2, -3), sabendo ofocoesté no
quado quadÍante,é paÍaeaaoeixo e o peÍâmetfo,
d y
p,é8.
Resolucâo:
p = I lndica
ouec= 4,ootsc r.
=
'2
As inlomaçôes pfoblema
do evam um esboço
a do
gÍáÍco:
tx - xv),= -4c(y - yv) t
Substtu x! = 0 e yv- 4 naeq!€ção,
ndo temósi /
[x - o)'= -4c(y a) = x'?= acty- 4]
Como p€rábola
a passa P[2 ]l vem
poÍ
2, = -4c[] 4l + 12ç=4=x-]
3
'ogo d equèGo pa-àbota
' o. e' - 1ti
3-' "t.
8. Vefíqle se os poíìtosA(3, 8) Btt, al, Cta, 2l €
D[ 8, - ]0) peftencern nãoà pâíábola devédc€
ou P
V[4,2]e foco F[],21.
R€solução:
A posição paráboa
dâ
indicaqueê equação é
Aposção pâéboe câquea
dê nd equação
é dafoÍna
la (y yv)'= actx- xvl. da foÍna (y yul =
= -4ctx xvl.
Daí,
vem
v( 2, 3l Peadistáncia V atéF
de
enconÌTarnos de c:
o v€tof
E( 2+4-3)-ç(2,-3) c = lt r 1 + I + t r r l, =
Dt-2 - 4,-31 + Dt-6, -3) Sabendo c = 3, = 4 eyv = 2, a eqlação
que da
dretfzx= -6 paébola éi
Substtu aslnformaçôêsfórrnLra,
ndo na ternos 0 yvl'z= actx x!1.+
6r - yvl'? 4c(x- xv)+ (y + 2), = 4. 4(x+ 3)..1
= = (y 2),= a.3tx - 4l + ty - 2),= -12(x ar
=
=ì (y + 2)'z l6(x + 3) A paftifdâ equação, podemos verfcaÍa posçãode
a tem ty =
Logo, paráboa eqlação + 2)'z l6tx + 31, cada dospontos rclação paÍáboa
!m €m à P
F(2, 3)edr€trzx= 6. At3,8l= t8 2l':l -12(3 - al =Ae P
Btr, -4) = t 4-2),:-12(1 4)=BeP
7. D€tem a €quaçâo parábola exode sirneta
ne da corn G[4,2] € P,pos é o véflc€da parábolâ
perpendicularao x, vértice ponto
eixo no V(0,4)e que D[ 8,-]01+ [ 10- 2)'= -12(-8 a)=
passa ponto
p€lo P(2,1).
/----;-;-- ---
erccros l
Dr000sÌ0s
: Detemìne equação paúboadêfoco e d retrzd
a da Í . Dadâsduas de =
paúbolas, eqLraçôesx,-l2ye
nosseguintescasos: x'?= 2y qualdelas concavidade
tem rnaor?Esboce
os
al F(9, e d:x = -g
0l c) F[0, e d:y - 7
7] gúfcospaÉcornprcvar Íesposta.
sua
b)Ft0,-6)ed:y=6 dlFt 5,0led x=5
DeÌeffnine
a equação paúbola
da quetern:
.;1,
DeterÍnineíoco, védce€ a d rctz'da parábo a
o o a, âl foconoponto 0] € difeviz equâção= -3;
F[3, de x
panir equações:
das b)diferfizde =
equaçãoy 3 evértceV(0, 0ll
a)Y'= 28x c) x, = lOy cl foconopontoF[],2l e difelriz equação= -2;
de x
i b)x'z=-4y dlv'= l6x d)difetdzdeequaçãox = 2 evértceV(-1, -3).

9. 78 À,Iâtemátkâ &Ap
' conÌêxto kàçÓer
Ê. DeteÍm ascoofdenadasfocoe a eouacãoda
ne do reta 7- A parábola equação - ôx + y + I = 0 intercecta
de x, o
dÌretrz parábo qle lêrnpofequação:
das as exox nospontos e B. Sendo o védlce pâúbolá,
A V dâ
a)*=4y
Lembre'se, exemp]o, que2 = ,(
[SugesÉo:
por
cl
de
'v
elx'?=
+)) deteÍnì ã árc€
nê
8, DêterÍnlne
doÍiânguoVAB.
a equaçâo paÍáboâs:
â) devéftice
das
VC-1,4), exopáfêlelo exoye quepassâ
áo
8',
b)y' = 2x dl p€o ponto A[3,0);
b)d€véfticeV(4,2) elocoF[4,s].
!ì Êncontre coordenadas vértce, cooÍdenadas
âs do as
doíoco, êquação rctâd Íetrze a equação eixo
a dâ do !]. Urna paráboâtenì noponto
loco F[3,]l e suadreÍlzéá
desirnet daspaúbolas eqLraçô€s:
a de rctâ eqloqão = -l, DeteÍrnine
de x a equação panábo-
da
a)y'z-6y- 12x+21= a a e os pontos quea retadeeqLração y = 0 nter.
em x-
f
b ) x'z- 2 x- y+4=0 sectâ parábo
a a.
Elipse
Origem
Vamos considerarum circular
cone reto,
Utílizândo plânoinclinâdo íelação eixoe que intersecte
|]m em ao todasas geratrizes cone,taíemosum
do
cortecomo rnostrâm desênhos
os sêguintes:
M Se phno
o for
Nessecaso,seccão
a cônicaobtidaéchamã elipse.
da
ffi tambémuma
é s€cção
a'-----ì
DeÍiniçâoe elementos
no doispontosfixos e F,talquea distânciâ
inicìalmente, planodo papel,
Consideremos, t, êntíe elesseja2c.
i;,
que
lmãgìne vàmosmarcar umaséie de pontostâl quê â somade suasdistâncias pontosfixosF, e F, seja
aos
constante maiordoque 2c,Naprática, podeserfeitocomo auxílio um lápis,
sempre e isso dê doisalfinêtes balbante,
e

10. GDft/lo , GmneÌÌia
3 (ônlcs
analírkarse((Ões
og ponto pontotêrêmos:
Construindo ráfico â
AFI + AF,=BFr + BF,=CFI+CF,=..,=JFr+JF r: . . . = L F I + L F , = . . . = 2 â (c o n s t a n t e ), s e n d o 2 a > 2 c
Aelipseéoconjunto dêtodos os pontosdo planoque satisíazem propriedade,
essa
Assim, que
definimos eiipsê o lugalgeoúétrico pontos um plano
é dos de tãlquea soma suas
de distâncias
a
doispontos fÌxo,,dênominados focos, e F2,seja
F1 constânter à 2aê maiorquea distância
igual entreos focos
(2a> 2c).
NafìguÍa,temos:
. Fre F,são focos elipsee distância eles a distância
da a entre é focal(2c)i
. ÃE éo eixo maiorda elipsee medidá ioma
sua éa queconsta defnição
da (2â);
. õrã;é o eixomenorda elipsêcuja
medidaé2b;
. O é o centro elipsê
da (intêrsecção eixos elipse pontomédio EE,Ã/l e EE,);
dos da e de
.6 6úrns16g ! ç66rn excentricìdade
= a-se (O
da elipse < ê < 1).
ObseÌv.çõesr
A excenÍicidad€
indlca quânto elipse
a
Í1) E;E= õÃ;, poisambostêmmedidaa. seaproxima um sêgmento de uma
de ou
circunfbréncia,
confonÌe vaÍor
se! sê
21) No notarque + c2= a2. relâção
b2 Essa éfunda- aproxlmà I ou de 0, respedÍv?mente.
de
^BrOFrpodêmos doselementos eìipse.
mentalnà
determinação da
Equaçãoda elipse
Vamosinicialmente consideÍar elipsecom asexremidades
a
do êixo maior nos pontosAÍ(-a,0) e Ar(a,0), do eixo menorem
81(0, e Br{0,-b)e, consêqüentemente,centroemO(0,0).
b) o
Considerêmos ponto P(x,y)qualqueÍdacuruâ.
um
Pela definiçãoobseryamos quê:
PFr+ PF,= 4F, + A,F,: A1A, 2a
-

11. . contsxto
lÏarsmátka &Adkãdes
DaLtemosl
(x c)'? (y
+ o)': (x+c) ' + ( y- o) '
+l*-.f +Y + l*+.f +y -2. *f,,+.)'+y =za-.,("-.y
+y
+( x+c),+y,-4a, +uf* .f +l +(x - c Ì + y ' : = +
=4a,+(x -c ),+
f -u* r f - S /
-+" .Ír -.)'*l -
= l "nft- .f 1. =4à'- I -2cx+ è -i 2<x d-
.f
/^J"- rf +v' = /^' - /cx = afi - ç1'., ç : ã2 cx+
-
= a,[(x- c), + y,] = (a, .- cx), a,[x, 2cx + c, + yz]: a4- 2a2.x+ c2x2
=]
-
_
.a a2x2 2t4+ a2<2 d2y2 a4 2ekr+ czx2 d2i) - c2x2 à2y2 a4_ a2c2
+ : + + : =)
= (a, - c,)x, + aty, : a,(a,- c,)
Naelipsetemos:
a2=b2+<2 =) d2 c1=b2
Substituindo equâçáo,
na obtemos:
b,x2+atr=arb2
lJmavezque + 0,vem:
ab
b'x' a'y' a'b' x' y)
ã'b' à'b' ã'b' a' tr'
emquea = oAr = oAr, c = oFr = oFrebtalqueb']= a'z c'?.
Essa
equôção denorÍltnada
é equoçáo do
rcduzida
eÍFse focosno êixox e centrona orìgem.
de
Vêjamos
agorai
í*" ,
seosfocosda sobreo y e o centro otigêm,
elipseestáo eixo na conformê
aíiguÍa,a
equação
reduzida elipse dada
da é por:
A rcciprocãverdad€ìÌ?:
é
y2
equações bnÌa , +
da = l,
b,
coÌÌ â + b Íeprc9êntâm ou
ellps€s,
ap€nas pontos uma
seja, os de elips€
stisftzem €s$ €quação.

12. GDÍh0l . Georìeíia
analíue:
se(çõe5
cônkas
Analogamente,
chegamos equações elipse
às da comcentÍoqualquer.
Asslm,
temos sêguintès
as equaçóês,
o centro pontoqualquer, yJ, e oseixos
considerando um O(xo, eixos e yi
Êatalelosaos x
'le)EE é paralelo eixo a = OA,, OB,e a>b.
ao I b: 2e)tE é paralelo êixo a : OA|b = OB1 a>b.
ao Ì, e
a í
{ ,
9. Detem a equação elpsede focosFr[3,0) e
ne da
F2[ 3, 0] e vériices, sãoas exÍernidades e xô
que dô
I
maiof,4[5, e A2[-5,0].
0J
Re8olução:
Pelosdados problema, focos
do os estão exo x e
no
r temosa=5ec=3,
a, = b, + c, + 25 = b2+ I ) b, = 16
(1,0)
Nesse caso, equaçìo
a reduzlda
é:
i:++=t=:+-L=l
a' h' 25 16
^,
€ oÍocuÍsda :: + -L = L
Looo. eouâcão é
25 16 ar=br+cr-ar=l+9=10
Como focos
os estão
localizados elxoye o vértice
no é
V(0,0l,temos:
'-. I-=t+:--L=t=t0Ì, r r=tú
b' a' 1 l0
Looo,aeouacão oÍocuÍâdaêx'z L = I oLr
+
10
Iox'z+Y'?: 10.
tl. Dete-Írine Íocos aseKrem
os e dades elo maoÍ oê
do
e ipse equação + 25y,= 100.
de 4x,
Resolução:
I O. Jna e iosetenos'ocós oonÌos 3)eF2(0.
nos Fr(0 -3) 4Ì'? 25v'? r00= 1
+ = + !!J- = !!!
Seo compÍrnenìo exomenoÍ elipse 2,deteÍm
do da é ' t00 100 100-
nea equâção dêssâelipse.
R66olução: 254
Peos dados problemâ,
do teÍnosl Como > 4, o eii(o
25 ÍÍ;ior esté eixo Então:
no x.
vto,
0l a'z=25+â=5
c=3

13. . ConrexÌoi(aóe5
MãremáÌl(a &Ap
a, = b, + cr:+25 = 4 + c,ì Resolução:
.-c'=21.)c=JÃ
al:+ z_=1
Logo, focos ospontos
os sâo 254
0J
F,(v2r e F,l i2r,0l e as
extrcm
dades exo maÌof
do são
c' = a2- b2= 25 - 4 = 2t = = tb
4is, 0)eA:t-5,01. "
r 2. corte,.noo o^o. (0. e r. (0. J:)eae.
os r, Jr e= ttt_1!9= osl
; 55
l
celtÍcid;de -
e , dFlerileaeoudc;odae
2'
Do( v 2
Resolução: 2 d
DeacoÍdo os dedos proberna,
com do teÍnos 2 I
5 0
5 0
+a=2c=2.Jí IB
2 - t,8
a, = b, + c, =12J3 | =b,+lJ3 l=
=12=br+3ãbr=9 bl
255
"gLrdo o. dêdos p obera os'ocoseslãoocê
do
y.
lzados €ixo Assm,vem:
no
'- '- - t-l )1^-3v-36 cr=25 9=16+c=4
rL
b'à'912 e=;_=0,8
oooa eoJacào
oÍocLÉdà
e '-t". 'v
912
4x'?+3y'z=36 0 3
13.lr-na e,pse. et'e-ldaoes e.oÌaor ;o os 0 3
as oo
ponrosAi[6,0] e A,[-6, 0]. Sabendo a e pse
qlre 5 0
p.s.apeopoÌo Pf3.2ì. dereïi'le { a equdçèo. 5 0
2 2,1
Resolução:
2
Pelosdados prcb€Ínatemos= 6.
do a
Corno eixo
o maoresüsobre exox, temos:
o
_+j_=lì_+L=l
a: b' 36 b' 25 t6
Corno eipsepassa ponto
a peo P[3,2),
temos:
941441
-l C=25-16=9+c=3
36b' 4h2b' 4
4 3 . t6 e=:=0.6
+-=-ã0?=- 5
SubstiÌuindoequação
na original,
vem:
,- 1^ -l-:: -:'L- ,1-2-l- 44
ã
orocuÍadaa r !4 =, o,
Looo. ecuacão
a li
36 16
4x'z+27y' 1=144
a.
t4,òacue a excenfrlcidade o esboço
do
gúÍco decadâelipse:
Êì-:-+r:l c)fi+r-t Obsêrvaçãot Ínaior
Quânto o
vaoÍ ce e = -, mats ma
prox
òe rm segmõnto a etipse
é
bìa+-L=l
'2a I

14. CapÍtuh. CêometÍã
3 a'ìalltka:iêqôêscôniaj 83
15. Deteffnine
â equâção elpsecorn
da centfo [2, - ]1,
ern Fâzendo = a? br,veÍn:
c,
exomaof2a= 6 € locoF1[0,
-]1. c,=9 5=4=c=2
Resolução: Daítemos:
dados probema
Pelos do a pos
identÍìcaÍìros çãoda Fli2- 2, l) = Frto,
l)
+
F2Q 2,1).+F2(41)
Logo,essa elipse centro
tern O(2,tl e locosF,[0,]l e
F,i4.11.
17. As equaçÕes seguintesÍepresenlam c rcuniefên-
urna
ca, urna paÉboae Lrma elipse.
ldentÍquecadauma
Daía eqmção: deas€ seltsprincpas elementos,
tr x"l' ty y"l' ê)y- Ãy-A' t 2-A
'r.= blx,+y,-4x 6y-12=0
Sabemos que clx,+2y,+6x+4y+7=0
2a:6=a=3 Resolução:
Calculando dstância centro(2, -1) ao foco
a do aly,+4y-Bx+12=0=
F1[0, venìl
-1], +f +4y+4=Ax 12+4.+
=
+(y + 2)'1 8x 8+6/+ 2l'= 8(x- r-
c=J(2-0).+[-]+t).=2 =
.+ (y + 2)'z a '2A. - ll [equação parábola)
de
Comoa=3ec=2,temos Dâíternos:
b,=a,_c,=9_4=5 vtr,-2)
SubsttLrndo dados eqlração,
os na vêrn
t^ *"1' ty y"l' Esboçando
o gúfco,vern:
fx - 21'l rv + tì':
| ô.ô Â êô ,.Âô .lpcc, p ó
^qp
lx - 2)' (y+D'
95
16-Aequdç;o5L or -20^ 8!- 6-0 ep eser-
ta urn8
elÌpse eixo
de pa€€loaoelxo Detem
maiof x. -
Resolução: Logo,a equação de Lrma
é paÉbolacom vétc€
Como Â,4, é pameoao exo x, devemos escfever
a Vl1,-2),c = 2 foco F[3, 2]edreüizx= -1.
eqìJação foflÌa
na b)x,+y,-4x 6y-12=o+
tx xnj- ty - y"J' =x,-4x+4+yr-6y+ I = 12+4+9+
.-d ".(x-2)'z+ ty 31,=25=5,
Desenvolvendoa equação dadã,
ternos: Logo, eqlação de urnâ
a é cifcuníeÉnca centfo
de
5x,+ 9y,_ 20x_ 18y _.16= 0 + C[2,3] faio
e 5.
+ 5x, 20x+ 9y' l8y = 16= c)x,+2y,+6x+4y+7=0=)
+ 5[x'z-4xJ g(y'?-2y)= ]6+
+ ..1(xÌ + 6x)+ 2(r'z 2y)= -7 )
+
=s[x'?- 4x+ 4) +901 - 2y+ ]) = 16+ 20+9+ .r l[x'z 6x+ 9] + 2M + 2y + 1) = -7 + I + 2
+
+ 5(x 2l' + 90/ rl, = 45 = =.ìl[x+3],+20/+ tl, = 4+
[x 2]' ty rl' Tr + ?ì'z r! + rì2
95
conc que:
Daequação, uírnos DaÍ,
têmos
centrcO[2,]l c(-3, 1l
Como 2,vern:
4>
6 ' . -2 = )b = 1 ,
c r= a r-b r= 4 Z = Z = " = rE
Logo,€quaÉodeurnã decentrc 3, ])
â é eipse C[
€ íocos FIC-3 Jí, 1.r"1 z+..1í. D

15. 8,1 G.
À,latemáÌContexto kadei
&AD
'ilC Detemine a equação elpse
dã conhecendo: X8" Detefinine€ lRpaÍa o ponto
que
k A[ 2, k] peilença
à
a)osfocos F1(3, e Fr(-3, 0) e o comprimênto
0) do gx'z
e ipse + 4y,+ l8x 8y - 23 = 0.
. elxo or:3;.
ma
^l: ^l:
, b)osvéÍtices Ã(5, 0l e At(-s, 0) e a excenticidade a )k = irjf : 611=41!!1
Jb 2?
5 ^1:
'! 1. Determine coordên6dâ6 íocoí âscoordeôadâs q 1 1 = 2 1 !^1: 4
l
e )k = -t rjl1
6s dos 22
dasextremidsdes maior a excentcidade
doeixo e das
e ipsesde equâ9ão: ^t-
c lt = 3 rjla
2
aì l+ ! = ì c)h,+f=2
Ì9"Aequâção9x,+4y,- t8x- t6y - | = 0édeuma
eìipse.0s semi-exos
maiofeÍnenofTnedêm:
' 25 I aj 4e3 dl3 e 2.
b)4e2. el3et.
i 2 0 eixo maiof umaêlpseestá
de no
conlido eixo Sa-
x. c)4e1.
bendo qle o côntro [0, 0], o comprirnento eixo
é do
menoré e a distâncbfocalé deterÍninea
6 10, equação 2C. A equaÉo e ipse passa ospontos
da qle pe [2,0] [-2,0]
0â orpse. e [0,]l é:
'Ìl::"
Quâlé medida exo maior (]ma
e do de elipse equa-
de a)x, + 4y,= 4
cão:+L=tt b lx , + ! = 1 .
'3625
c )2 x , -4 y , = 1
1lr. Doisdosvértices um quadiláteÍo os focos
de são da
elipse equação + 5l = 20.Osoutros vérti
de x'z doÌs ?1. Encontreequaçào êlipse
a dâ sbairo:
cessãoasextremidadeseixomenor elpse.
do da Cal
cule áÍea quadflátero.
a do
Ì 5" Emumaelipse, centroé (-2, 4), um dosfocosé
o
l-2. 7) e umadas extremidades eixomenofé
do
[-3,4). Detemine equação
a dessaelipse.
i 4- quais asextremidâdeseixo
são do menor €lpsede
da
equaçãox, 4y, - 4x - 8y + 4 = 0?
+
ll Dsdâsâsêliosês:.L = ìê
+
94
^ "r + r' 'r - L oJa delasrem maiorex-
83 22. A reta = âx+ I intercepta
y aelipsex, 4y,= 1sornen-
+
centricidade? tenum ponlo.
Carcule 8s7
Flipérbole
0rigem
Vâmosaonslderôr cone
um duplo
um plâno qualquêtque seccione
e
as v
duasfolhas coneconforme
do mostrâm i/-*
â5fi9uÍas:
/
,D

16. (aDítulo3'6e0metdaanaiílka:5ecôes.ônkõ E5
Nesse obtidaé denominadahipétbole.
caso, seccáocônica
a
ir;içâr:; *tr*mentos
r:
Iniclalmente, pontosfixos, e F2,de planocuja
Consideremos, dois Fr uín d(Fr,Fr)= 2..
distânciâ
q
lmagine uevamosmôr€ar 5ériede
uma pontos planotalque
no
(em
a diferença móduio) suas
de distâncias pontos
aos fixosFr e F2
sejasempre constantee
menorque Na2c, práticâ, pode feito
isso ser
como âuxlliodêrégua,lápis,
alfìnetese barbante.
= ...: lTFr TF,l:2a (constânte),com< 2c
- 2a
O aonjunto todoi 05pontosdo planocome$a proptledâde
de dama-3êhip{ròoL.
|_-2.-'---__'-j

17. Assim, definimos que hipérbole o lugârgeométrico pontosp(x,y) de um plânotal que a diferença
é dos (em
módulo)desuâs dÌstâncias doispontosfìxosF1e F2é constãnte < 2c),com F,F,= 2c.
â (2a
NafìguÍa,temos:
. Fr e Fr,osfocosda hipérbole,sendoFrF,: 2c a distâncja
focal;
.4, e A2, os vérticesda hipérbole, sendoArA, = ArF, AiFr = 2a (constânte da
definição);
de I br a eÌcentricidade,
. O,o ( enFoda hiperbole tponro nèdio de E e de A 4)j
. o númeroe = que é a excenÍicidade hipérbole
da (notequê e > t, poisc > a). panÌelas [perp€nd'cuhres
;, ao eixo rêaÌ]. sea
E
Observação: Considerando umâ hipérbole focosF1e F: e védces A1e A2,vimos
de
=
queFrF: 2ce ArA,: 2a.Então, : c e OA,= a.
OF:
âo ÌnÍìnÌto, hÍpérbole
à
semtsEras
oposrãs
tcom
. Nasmesmas condlçõ€s
d€ BrexisteBr,sobrea
mediatriz Ãô,taÌ
de
qu€ = 2b.
qB,
Seja81 um ponto da mediatriz ÃE tal que o triânguloBrOA,sejaretángulo
de . aôe cnamaao
em O, como catetoõÃ medindoa e a hipotenusa
ú- mêdindoG.
Assim,
chamando eixoEate , eixa
in agínérlo da hipërbole.
de b a medidâdo catetoõEì, temosà: + b, = c, ou b2= c2- â2.
Equação hipérbole
da
ConsÍderemos inicialmêntea
hipérboledaÍigura,
naquâl05focos
penencem eixox e o centroéa origêmO(0,0),
ao
Um ponto P(x,y) qualquerdã curvadeve sãtisfazer, acordo
de
com â defìnição, seguinte
a condição:
:2a
lPF, PF,l
-
ComoPF,: (x+cf +(y o F (x - c)'z (y o)':, temos:
+
(x c)'z+y':l=2a+ (x -c )' z + y ' )
(x c)r+y'?t2a
Elevando
âmbosos membros quadÍâdo,
ao vem:
(x + c ) r + y ' z : ( xct+y,+4 a J(x-c)2 +y')+4a,.r ( x+ c) ,+ y, c|, y,- 4^,= touf , -
lx- 4, + I =
L{t2cx (tl { 2<x-1 y' -4a, --4a,,lt <t-y-
+ ccx- qa'= t+aü;õt+7=." u, : t"14-ã, +I

18. (apítulo3'CeonìèÌflaanaliÌG:ç((oe5dnkõ 67
novamente, doismembíos quadíado,
Elevando, os ao obtemo5:
crx, 2alcx+ aa= azf(x c), + t'l) crx,_ 2arcx+ aa: ar[x, 2cx+ c, + yr]r
+crx, aa+r+ â4 = arxz_bkr+ a2a2 a2y11Cxz_ a2x2 a2y2: a2a2 a4:-
+ -
:+ (c, - ar)x,- aryz: ar{c, a1
cr:ar+br=cr,âr=b,
(c'?
Substituindo - a'?) equação
na anterior, - :
temosb1'1 a'1yz a'zb'1.
Como *0,vem:
ab
b'r' à-y' a'b'l ,l' ,'
;b r ;b r-a ,b- - J- br - i
em quea: oAr : oÁ2, oFr = oF, e bé talque b2:.2 a2.
c:
Essa equoção
íórmulaé denominadã da quandoosfocosestáosobreo eixox e sãoeqüidis
rcduzida hipéóole,
tãntesda origem.
Vejaagora:
A rccÍprocâ veÌdadeira:
é
Casoosfocosestejâm reduzida hipérbole
sobíeo eixoy, a equação dâ será:
ÌEpÌEsent hipérbolet
m
satlsfâ?em êquação,
esla
podemos
Anâlogâmente, generalìzaressaequaçáopaÍâ
um centfoqualquer,
Considerãndo (reâle
o cenÍo da hipérboleO(xdyo)eoseixos imaginário)paraleÌos
aoseixosxey,temos:
1-')Eixoreaiparalelo eixoxl
ao 2-')Eixorealparalelo eìxoy:
ao

19. 18. Detennine equação hipérbole íocos
urna da de Fr[b,0) Como focos
os estão ye
sobre eixo O[0,0),venì]
o
e F2f 0)ederérlie34,(3.01eA,í
-5 3.01.
Rè9oluçãor ã'b'97
Pelos
dados proberna,
do t€Ínos
Logo,J-rê poLaçào lperooe e '-
d" - 0.,
a:3
7y, 9x2= 63.
c, =a, + br325 = 9 + br=b, = 16
CoÍno focos
os estão
sobre exox, vem
o 21. Uma pérbo tern
h e locos pontos
nos Fr(3,0) e
,_
j_= t 3_
-= t+
F,[-3,0] e passâ ponto
peo Ph6,2) r
+ l6x ' ?- gy ' ? 1 4 4
: qualéa eqLragão h pérboe?
dessa
Logo. a eo -a ç ã o é h o á o o e é +
ur o " ^ - ' o-
_
l6x ' z gy ' z 1 4 4
=
19. Deteffnine
um€equação hipétuote
da defocosFr[6 0]
e F.[-6 0l e de e^centÍic
dade oua a9
?
Rêsolução:
Resolução:
CoÍÍoos focosestãosobÍeo exo x e o cerruo
eÍrì
(0,01,
ternos:
:- l= = t
Como hipérbote
a passa ponto
pelo p[16,2), vern:
Peos dados prcblema,
do temos:
c=ô r-Ãr,
" -, -l :1= ì3 4 _:= r fò
3 c 3 2c 2.6 a' b'| a' b,
e:-:+-=-=a=-=-=4
2a2 =
C ornoc, a, + b, ec : 3,obternos:
c?= a, + br336 = t6 + br+br: 20
9 = s ' + b r= a r= g b , (D
Cqmo focos
os estãosobre eixo O[0,0),vem
o xe
(D O,
Substtuindoem temos:
:. J--t-." Y- -trrÀ. /v/-80
a' b' t6 20
I oqo,Ln; eq-a(ão hioéooh e I -- l -5b) 36 1/o-goi -o-
da
'162A - I - .u
-
5x'?-4y'?=80. +h'+ú+A!í-9{ 26=o=è
2O.Um€ hpérbole tocosnos pontos
têm F,[0,4) e +b4-36=0+b{=36.+br:6
Ír[0, -4]. O segrnento
Ã8, châÍÌìado trarìsver
eixo
[4âs
sâl[o! real),tem
coÍnpdmefto Det€rm]ne eqra
6. urna
çãodessa hipéúole. a'z=9-br=9-6=3
Rôsolução: SubsÌitu €sse
ndo valofnaequação
feduzidâ hipéf.
da
Pelos dâdos pÍoberna,
do temos bole,
vern:
2â:6.+a=3, x': v'z
-.e -,-21 -r1 _a
r > compírmeito êlxonansvêGô
dÒ ; tr-,=:
C:â,+b,+16=9+ br=
Logo,a equação hipéÈole
dâ é: -1- = 1 ou
2x2 y2:6.
-
22, Determ o centro, locos osvértices h percoe
ne os e da
de equação - y, + t8x + 8y + 38 0.
3x, -

20. opílulol . Gúmel mãlítka:s.iôes
ô (ônicaj 89
Resolução: Resolução:
TÉnsíoÍmando nlciâlmente tenìos:
a equação, gx'z l6v: = 144+ ::_ - lil = lll +
'
3x, y, + l8x + 8y+ 38 = 0.ì 144 144 144
x2 '
= 3[x'z+ 6x] - 6/'z 8yl = -38 +
-
t6 I
=3[x,+ôx+9]- [jl-8y+ ]6)= -38 + 27- 16+ Aeqmção ndic€qlreosíocosestãosobreo eixox com
=3[x+3)'?-]0-4)'z:-27+ centrot0. 01,daí:
+ ][y 4)'z- 3[x+ 3]'z=27+ a' := 16= a = 4
ty al' [i + 3]'?
cr= ar+ br-t6+ 9= 25âc= 5
279
Daequação obtida,
vern:
c5 t
a4
centro:o[ 3,4)
Logo,Fj(5, 0l e F,[ 5, 0], 4[4, 0] e A,[-4, 0] e a ex-
a'=27=a='Eì:3E .5
b ' z = e + b = Jt=3
c, = a, + b, = 27 + I = 36.+ c = 6
25, DeteÍnineaequação hipéÍboe ceftro[3,5],com
ds de
umdosvéftcesem[], 5l e umdosíocos [- 1,5).
eÍn
Resolução:
pelosdados prcblenla, exo rcalda h pérbo é
do o e
para o aoexoÍ clja equaçãodaÍorma:
e é
tx - x.l, ty y"l,
Logo, hpérboe centro
a tem O(-3,4), vénices
dr i=
i - :.. :"6ìeí 3.c 3"6ìeroLos,
3.ror .
Fazendo esboço hpérboe,
Lrm dâ ternos:
t-3, - 21.
23. Emurna hipérboe centro
de O[5,5],a disúncaíocalé
2c=6eoeixofea2a= 2 é paÊeloaoe xox. Delef-
rnine equação
a dessahipérbole.
Resoluçãor
Doenunciado,vern:
CenlrciO[5,
5]
a=3-1-2
2a=2=a=1 c:3-[ ]l=4
br=cr_a2=3r_tr=8 b,:c, ar=16_4:12
Seo eixo é paralelo €ixo a equação dotlpo:
reaì ao x, é Slbsütuìndo d€dos fóÍnúla,
os na obteÍnos:
(x ly - y,)' ir x,), (y y"l,
^"1' ='-
t r ,.
ooo, eouacão''
a e "' t ') - 1 t^ 3Ì [y s]'
t8 412
gx'? I6y'z 144 Deter-
= prccurcda
Logo,equ€ção
a é
24" Umah páboe ternequ€ção
nìne as cooÍd€nadas íocos, cooÍdenâdâs
dos as dos (x 3l' (v - sl'
vértjces a excentdcdade h péÍbo
e da e 4W =

21. pÍopostos
[xer(kios ]
Deteffnine equação hipéúole,dados:
a da :lÍ.J.NuÍnahpérboe gud
deexcenÍicidade â a6, osveftrces
al os locosF1 0] e F,(- 8 0l e os véd cesA, [5, 0] e
[8, sãoos pontos 0] e Ar(-2, 01.Deteffnine coor
as
4[2,
4i 5,ol oenadês seus
de focos.
bl osvátces 4(3, 0) e A,[ 3, 0] e a d stánciâ
entr€
osíocos iguàla 8;. :;S Considercnrosa hipéfbole eqlação4y, - x, = 16.
de
cl osvéllcesAt[3, 0) e 4[ 3, 0] e a excentricidâde qualé€ equação urna
de cifcunfeÉnca centro
cujo coin
Quata2 cde corn centrc hpérboee qlr€passa
o dâ pelos
focos
dâ hipéÍbo
e?
Determ ascoordenadas focos, coofdenadas
ne dos âs
dosvértices excentctdêd€ hipéúolesdaseqLra::'I Calcua exc€nÍic e = 9. esboce codemda
ea das e dade o oráf t
çÕes ãa
a) 4x' - 25y'= 100 urna hipérboles
das e reacone vaÌof e com Íes
o de a
pectiva
Ígura:
hì: l =l
-'t6 25 aJ -r=r cl:-l=l
f cr:x':-ayz 36 = r t3
l
neaequação hipéfboleque peopon-
da passa
D€t€mì t5
P(qr,ã, e tem ós focosnos ponros
sl F1[5.0) e
"Jo DFle-Íri'ì- d equdç o ad hp. oop cLjo. rocos sao
F,t 5,01. Frt3,6l €F,t3, 6l eoexo magi náfoé2b 6=
Cacu o compriÍìento s€gmento los pontos
e do 4,4 Quele a o,sl a' ìcéocdl hoeooe c a eqra áo e
AÍ e A, sãoüs védceslnumahlpéúole equaçao
de "
4x' ? 251 32x - t00y 136= 0?
4x'-25y'1=100.
:'3,0 centro urna
de hÌpérboe o ponto[4, -3), seuexo
é
,ocLle êlo demodda "êhto-oo"d-eq-aç;o
o rcâlé 2a = 6 e o etxoirnagnárlo 2b = 4. Deternìine
é â
p(í]5, equação dessa hipérboÌeseus
€ focos e F2,sab€ndo
Fr
, " + = l passep€oponro 41. que
_ârnda iF, ó pãÍâielo eixo
ao x.
Assíntotasda hipérbole
Vamos
consideraía
hipérbole". l. . de cenLro origem eixoreàlhorizontà|.
na e
b'
y
lsolando nessâ
equação,
obtemosì
, y) x h À-
' -
t-y =:rx - à':)ry=-"Jxr-à-
D- A_
Vamosobservar agorao termo x, - a2que estána raizquadrada.
--, poisé um valorfixonâ
Nelê, é constante,
a
hipérbolê,masx é variável, seja,
ou paracadaponto peatencente hipérbole,
a xassumirá valorrealdiferente,
um
Então,vamosimaginârxassumindo valoresmuito aíastados centroda hipérbole.
do Essesvalorescorrespon-
deriamã pontosdascuívâs maise maisdistantes A. e 4..
de
que
À medida x assume valores cada mdiores
ver rno;entido posirìvo eiro dasabscisiasl cadavezme-
do ou
nores(no sentidonegativo), diferença
a x, a?vaise aproximando cadavez maisdo própriox2,já quê â2,sendo
quasedesprezível
constante,fica pertodexr.
Porexemplo, â = l, teremos:
se
2 4 3
20 400 399
2 000 4000000 3 999999
e assimpordiante.
podemos
Então, que,paravalores
consideraí muitograndes, muito pequenos xfor negativo, quadra_
ou (se ao
do ficdposkivoeà
diferença mesmd),a b b
eè equaçáo hipérbole -.
dà y ,,,ç J ,.uproxima
dey - - Vx, e,
h
portânto, y: Aax que sãoretas
de qu€ passampelaorigeme têm,respectivamente,
declividades:q e lq.

22. (apílülol. G-Àomêtíiianàlitkã:se.!óesónicõ
A essasÍetâsdâmoso nomêdê asJírfotatque sãoas retasparaâsquaistendea curva,emboÍanuncaasto-
quem (poiso pêquenoâ2sempreestârá presente).
Nográfico podemos
de5sa ipérbole,
h facilmentedeterminâpontosdessa
r reta,constÍu
indoo rêtâ ulo IM PQ
ng N
que passapelospontosAl'42' 91e Br:
observequeasdiagonais
desse I
retángulo retasde declividades
são e 9, respectiuamente.
Deagoraem diante, paratraçarmosográfìcodeumat'iperfotepoaenios ndo asassíntota(bâs-
coï'eçar trãça s
ta ter os valores a, b e as coordenadas centro)e depois, mão livre,conduziÍmos duascuruas
de do à as que coÍn-
põema hipérbole, semchegaratocaressas retas, as
masaproximando cadavezmâisdelas.
Generalizando, equaçoes assrntotas
as das seráo:
h
y - yc = r:(x - xc) Geoeixorealfor
horizontal)
".1 .
- xc) (seo eixoreaI for vertical)
26. De.err a. eo açdes p-r asïnrorês h oeroo deeor,aÇao
re oas da e -'
0,5
Resolução:
Daequação,vem
ots,zl
fcentro
]a'=64=a=8
b'=36+b=ô
Lexo horzontal
Íea
Equações assíntòks:
das
4y- 8 = 3x - I 5 + 3x - 4y- 7 = 0
A /
v ,=+-:fr 5ì
' -8 - .y
r- ,,. b-3r r4 )-z i-o
as das assíntotas 3x - 4y - 7 = 0 € 3x + 4y - 23 = 0.
Logo, equações retas são