Presentation.key
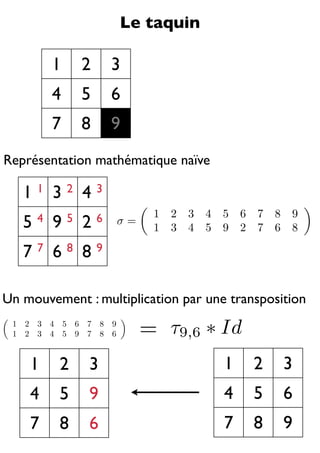
- 1. Le taquin 1 2 3 4 5 6 7 8 9 Représentation mathématique naïve 11 32 43 1 2 3 4 5 6 7 8 9 5 4 9 5 2 6 σ= 1 3 4 5 9 2 7 6 8 77 68 89 Un mouvement : multiplication par une transposition 1 1 2 2 3 3 4 4 5 5 6 9 7 7 8 8 9 6 = τ9,6 ∗ Id 1 2 3 1 2 3 4 5 9 4 5 6 7 8 6 7 8 9
- 2. Propriétés de cette représentation 1 2 3 1 2 3 4 5 6 7 8 9 4 5 6 σ= 1 2 3 4 5 6 8 7 9 8 7 9 σ résoluble ? Si σ résoluble, σ = τ1 τ2...τp Alors, ε(σ) = (-1)p Parité de p récupérable : Problème : Démo de ε(σ) = (-1)p σ résoluble 1 2 3 4 5 6 7 8 9 5 1 2 σ= 5 1 2 7 4 3 6 8 9 7 4 3 ε(σ) = 1 6 8 9 Résoluble ?
- 3. Autre représentation Classe d’équivalence : 1 2 3 6 5 4 7 8 Numérotation suivant le serpentin Représentation d’une configuration : 5 1 2 51 12 23 Exemple : 4 3 76 45 34 7 6 8 67 88 1 2 3 4 5 6 7 8 σ= 5 1 2 3 4 7 6 8
- 4. Résolution du taquin Représentation d’un mouvement : 1 2 3 1 2 3 Exemple : 6 5 4 5 4 7 8 6 7 8 1 2 3 1 2 3 5 7 4 5 7 4 6 8 6 8 1 2 3 4 5 6 7 8 τ5,8 = 1 2 3 4 6 7 5 8 Mouvements possibles : 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 τ1,6 = τ2,5 = 5 1 2 3 4 6 7 8 1 4 2 3 5 6 7 8 1 2 3 4 5 6 7 8 1 2 3 4 5 6 7 8 τ5,8 = τ4,9 = 1 2 3 4 6 7 5 8 1 2 3 5 6 7 8 4 Et leurs inverses… Ces permutations génèrent un groupe
- 5. Algorithme SIFT Permet la décomposition d’une permutation en produit de générateurs du groupe. Pour le taquin, on a une permutation et les générateurs : on utilise SIFT ! Étude des isométries laissants invariantes les quatre points d’un carré : 1 • •2 4• •3 Exemple : R-π/4 4 1 • •2 • •1 4• •3 3• • 2 1 2 3 4 R−π/4 = 4 1 2 3
- 6. Tableau de permutations Exemple : Id - Id σ • σ(1)=1 • σ(2)=4 - - Id • σ(3)=? - - - Id Tableau permutation : • La case T[i; j] est : • soit indéfinie, • soit contient σ telle que • ∀ k<i, σ(k)=k • σ(i)=j
- 7. SIFT 1 2 3 4 1 2 3 4 Générateurs : R= 4 1 2 3 S= 3 2 1 4 1 2 3 4 σ= 3 4 1 2 Id S R - Id La place est prise pour σ ! - - Id - - - Id SIFT : 1 2 3 4 γ = S −1 σ = Id R3 S R 1 4 3 2 - Id - ɣ 1 2 3 4 - - Id - R3 = 2 3 4 1 - - - Id Tableau complet de calcul du groupe G : • Tableau de permutation • ∀ ε∈G, on peut écrire ε = σ1σ2σ3...σn où σi appartient à la ligne i du tableau.
- 8. Résultats sur le taquin (P 04 09) (P 04 09)i 5 mouvements au départ, SIFT donne : (P 01 06)i*(P 04 09)*(P 04 09)*(P 04 09)*(P 04 09)*(P 05 08)* (P 04 09)i*(P 04 09)i*(P 04 09)i*(P 04 09)i*(P 04 09)*(P 05 08)i* (P 04 09)i*(P 04 09)i*(P 04 09)i Simplifiable : (P 01 06)i*(P 04 09)*(P 04 09)*(P 04 09)*(P 04 09)*(P 05 08)* (P 04 09)i*(P 04 09)i*(P 04 09)i*(P 04 09)i*(P 04 09)*(P 05 08)i* (P 04 09)i*(P 04 09)i*(P 04 09)i (suppression des identités) (P 01 06)i*(P 04 09)*(P 04 09)*(P 04 09)*(P 04 09)*(P 05 08)* (P 04 09)i*(P 04 09)i*(P 04 09)i*(P 05 08)i*(P 04 09)i*(P 04 09)i* (P 04 09)i Objectif pour étendre : trouver d’autres simplifications
Notes de l'éditeur
- \n \n
- \n \n
- \n \n
- \n \n
- \n \n
- \n \n
- \n \n
- \n \n
