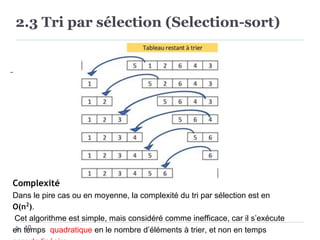
Le document traite des algorithmes de tri, en expliquant plusieurs méthodes, dont le tri à bulles, le tri par sélection, le tri par insertion, le tri fusion et le tri rapide. Chaque algorithme est décrit avec son principe de fonctionnement et sa complexité en temps. Les algorithmes de tri sont cruciaux pour organiser efficacement les données et améliorent la performance des algorithmes de recherche.

1. Algorithmes de Tri
Dr BEN-NAOUM Farah
1
Université Djillali liabes
Département d'informatique

2. 2.1 Présentation
2
• Ordonner, ranger, trier un nombre considérable de
données sont des opérations fastidieuses pour un être
humain, alors qu’un ordinateur est bien plus efficace
dans ces tâches répétitives. Il existe de nombreuses
manières de programmer un ordinateur pour trier des
données. Ainsi, les plus grands informaticiens se sont
penchés sur la question afin d’élaborer des algorithmes
de tri les plus efficaces possibles.
• Un algorithme de tri est un algorithme qui permet
d’organiser une collection d’objets selon une relation
d’ordre déterminée. Les objets à trier sont des éléments
d’un ensemble muni d’un ordre total. Les algorithmes de
tri sont utilisés dans de très nombreuses situations. Ils
sont en particulier utiles à de nombreux algorithmes plus
complexes dont certains algorithmes de recherche,
comme la recherche dichotomique.

3. 2.2 Tri à Bulles
(Bubble-Sort)
3
Le tri à bulles ou tri par propagation est un algorithme de tri. Il
consiste à comparer répétitivement les éléments consécutifs d’un
tableau, et à les permuter lorsqu’ils sont mal triés. Il doit son nom
au fait qu’il déplace rapidement les plus grands éléments en fin de
tableau, comme des bulles d’air qui remonteraient rapidement à la
surface d’un liquide.
Principe :
✔ L’algorithme parcourt le tableau et compare les éléments
consécutifs.
✔ Lorsque deux éléments consécutifs ne sont pas dans l’ordre, ils sont
échangés.
✔ Après un premier parcours complet du tableau, le plus grand
élément est forcément en fin du tableau.
✔ répéter les parcours du tableau, jusqu’à ce que les deux plus petits

4. 2.2 Tri à Bulles
(Bubble-Sort)
4

5. 2.2 Tri à Bulles
(Bubble-Sort)
Une optimisation consiste à l’interrompre dès qu’un parcours des éléments
possiblement encore en désordre (boucle interne) est effectué sans échange.
En effet, cela signifie que tout le tableau est trié. Cette optimisation nécessite
une variable supplémentaire.
5

6. 2.2 Tri à Bulles (Bubble-Sort)
Exemple
soit la liste (5, 4, 2, 3, 7, 1), appliquons le tri à bulles sur cette liste d’entiers.Visualisons les
différents états de la liste pour chaque itération externe contrôlée par l’indice i :
6

7. 2.2 Tri à Bulles
(Bubble-Sort)
Complexité:
✔ Pour le tri, la complexité en temps est de O(n2
), avec n la taille du tableau.
✔ Le pire cas (n itérations) est atteint lorsque le plus petit élément est à la fin du
tableau. La complexité est alors O(n2
).
✔ En moyenne, la complexité est aussi O(n2
).
✔ Le meilleur cas (une seule itération) est atteint quand le tableau est déjà trié. Dans
ce cas, la complexité est linéaire O(n).
7

8. 2.3 Tri par sélection (Selection-sort)
8
Principe:
Le tri par sélection est l’un des tris les plus instinctifs. Le principe est
que pour classer n valeurs, il faut :
✔ Trouver le plus petit élément et le mettre au début de la liste
✔ Trouver le 2ème
plus petit et le mettre en seconde position
✔ Trouver le 3ème
plus petit élément et le mettre à la 3ème
place,
✔ Trouver le ième
plus petit élément et le mettre à la ième
place,
ainsi de suite...
L’algorithme se termine quand i = n, (il n’y a plus qu’une valeur à
sélectionner ; celle ci est alors la plus grande valeur du tableau.)

9. 2.3 Tri par sélection (Selection-sort)
9

10. 2.3 Tri par sélection (Selection-sort)
Complexité
Dans le pire cas ou en moyenne, la complexité du tri par sélection est en
O(n2
).
Cet algorithme est simple, mais considéré comme inefficace, car il s’exécute
en temps quadratique en le nombre d’éléments à trier, et non en temps
10

11. 2.4 Tri par insertion
(Insertion-sort)
Principe :
✔ Commencer par le deuxième élément,
✔ Comparer l’élément choisi avec tous les éléments précédents dans la
liste et l’insérer à la bonne place de sorte que la liste formée par les
éléments traités reste toujours triée.
✔ Répéter les étapes 1 et 2 jusqu’à traiter le dernier élément de la liste.
11

12. 2.4 Tri par insertion
(Insertion-sort)
12
Exemple
Voici les étapes de l’exécution du tri par insertion sur le tableau
[6,5,3,1,8,7,2,4]. Le tableau est représenté au début et à la fin de
chaque itération.
i = 1 :[6,5,3,1,8,7,2,4] →
[5,6,3,1,8,7,2,4]
i = 2 : [5,6,3,1,8,7,2,4] →
[3,5,6,1,8,7,2,4]
i = 3 : [3,5,6,1,8,7,2,4] →
[1,3,5,6,8,7,2,4]
i = 4 : [1,3,5,6,8,7,2,4] →
[1,3,5,6,8,7,2,4]
i = 5 : [1,3,5,6,8,7,2,4] →

13. 2.4 Tri par insertion
(Insertion-sort)
13
Complexité
La complexité du tri par insertion est O(n2
) dans le pire cas et en moyenne,
et linéaire dans le meilleur cas.

14. 2.5 Tri fusion
(Merge-sort)
14
Principe et Exemple
Le tri fusion est construit suivant la stratégie ”diviser pour régner”, en anglais
”divide and conquer”. Le principe de base de la stratégie ”diviser pour régner”
est que pour résoudre un gros problème, il est souvent plus facile de le diviser
en petits problèmes élémentaires. Une fois chaque petit problème résolu, il n’y
a plus qu’à combiner les différentes solutions pour résoudre le problème
global. La méthode ”diviser pour régner” est tout à fait applicable au problème
de tri : plutôt que de trier le tableau complet, il est préférable de trier deux
sous tableaux de taille égale, puis de fusionner les résultats.
L’algorithme est récursif. En effet, les deux sous tableaux seront eux même triés
à l’aide de l’algorithme de tri fusion. Un tableau ne comportant qu’un seul
élément sera considéré comme trié : c’est la condition d’arrêt. Etapes de
l’algorithme :
✔ Division de l’ensemble de valeurs en deux parties
✔ Tri de chacun des deux ensembles
✔ Fusion des deux ensembles

15. 2.5 Tri fusion
(Merge-sort)
15

16. 2.5 Tri fusion
(Merge-sort)
16

17. 2.5 Tri fusion
(Merge-sort)
17

18. 2.5 Tri fusion
(Merge-sort)
18

19. 2.5 Tri fusion
(Merge-sort)
La récurrence définissant le temps d’exécution d’un algorithme
diviser pour régner se décompose suivant les trois étapes du
paradigme de base :
1. Si la taille du problème est suffisamment réduite, n <= c pour une
certaine constante c, la résolution est directe et consomme un
temps constant O(1).
2. Sinon, on divise le problème en a sous-problèmes chacun de
taille 1/b de la taille du problème initial. Le temps d’exécution
total se décompose alors en trois parties :
a) D(n) : le temps nécessaire à la division du problème en
sous-problèmes.
b) aT (n/b) : le temps de résolution des a sous-problèmes.
c) C(n) : le temps nécessaire pour construire la solution finale à
partir des solutions aux sous-problèmes.
19

20. 2.5 Tri fusion
(Merge-sort)
Finalement, le développement de cette formule récursive nous amène à une
complexité au pire des cas en O(n.log2
n).
20

21. 2.6 Tri rapide
(quick-sort)
L’algorithme de tri rapide, ”quick sort” en anglais, est un algorithme de
type dichotomique. Son principe consiste à séparer l’ensemble des
éléments en deux parties. La différence par rapport au tri fusion, vu
précédemment, est que la séparation des différentes valeurs ne
s’effectue pas n’importe comment. Pour effectuer la séparation, une
valeur pivot est choisie. Les valeurs sont réparties en deux
ensembles suivant qu’elles sont plus grandes ou plus petites que le
pivot. Ensuite, les deux ensembles sont triés séparément, suivant la
même méthode. L’algorithme, est récursif, mais cette fois, il n’est pas
nécessaire de fusionner les deux ensembles. Le résultat du tri est égal
au tri de l’ensemble dont les valeurs sont inférieures au pivot
concaténé à l’ensemble des valeurs supérieures au pivot, ce dernier
étant pris en sandwich entre les deux ensembles.
21

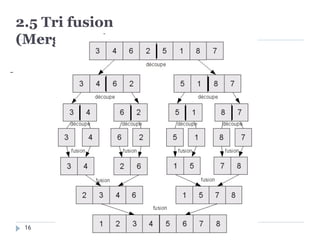
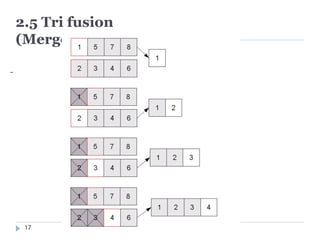
22. 2.6 Tri rapide
(quick-sort)
Le principe du tri rapide est le suivant, étant donné un tableau de T[1,
..., n] :
– si n=1,retourner le tableauT.
– sinon :
• Choisir un élément du tableau, élément que l’on nomme ensuite
pivot.
• Placer le pivot à sa position finale dans le tableau : les
éléments plus petits que lui sont à sa gauche, les plus grands à
sa droite.
• Trier, toujours à l’aide de cet algorithme, les sous-tableaux à
gauche et à droite du tableau.
(plus de fusion !)
Pour que cette méthode soit la plus efficace possible, il faut que le pivot
coupe le tableau en deux sous-tableaux de tailles comparables.
22

23. 2.6 Tri rapide
(quick-sort)
23

24. 2.6 Tri rapide
(quick-sort)
Exemple
Par exemple, pour trier [101, 115, 30, 63, 47, 20], on va avoir
les itérations suivantes :
[101(i), 115, 30(p), 63, 47, 20(j)]
[20, 115(i), 30, 63, 47(j), 101]
[20, 115(i), 30, 63(j), 47, 101]
[20, 115(i), 30(j), 63, 47, 101]
[20,30(j), 115(i), 63, 47, 101]
Et on relance le processus sur les deux sous tableaux [20] et
[115, 63, 47, 101]
[115(g), 63(p), 47, 101(d)]
Complexité
En moyenne et en meilleurs des cas, la complexité est en O(n
log(n))
24