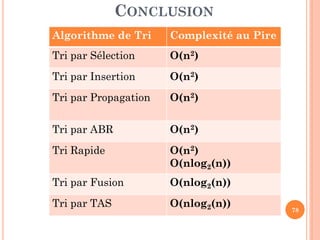
Le document est un cours sur les algorithmes de tri enseigné à l'Université Saad Dahleb de Blida, détaillant divers algorithmes tels que le tri par sélection, par insertion, par propagation, par fusion, rapide et par arbre binaire de recherche. Chaque algorithme est présenté avec son principe, son fonctionnement et sa complexité analytique. Le cours vise à concevoir ces algorithmes de manière récursive et à comprendre leur performance en termes de complexité temporelle.

1. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE IV:
ALGORITHMES DE TRI
Cours n°7: 30 Octobre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. PLAN DU CHAPITRE IV

Introduction

Tri par Sélection

Tri par Insertion

Tri par Propagation

Tri par Fusion

Tri Rapide

Tri par ABR (Arbre Binaire de Recherche)

Tri par TAS

Conclusion
2

3. INTRODUCTION

Étant donné un tableau d’entiers T (n: sa taille),
l’algorithme du trie permet d’organiser les éléments du
tableau selon un ordre déterminé (croissant par exemple).

Plusieurs algorithmes de tri existent: tri par sélection,
par insertion, par bulle, par fusion, rapide, par ABR et
par TAS.

L’objectif de ce cours est de concevoir ces algorithmes de
tri de manière récursive, ensuite, de calculer leur
complexité.
3

4. TRI PAR SÉLECTION
PRINCIPE

Le principe est de rechercher la plus petite valeur et la
placer au début du tableau, puis la plus petite valeur
dans les valeurs restantes
et la placer à la deuxième
position et ainsi de suite...
7
3
18 13 7
3
7
7
13 18
3
7
7
13 18
7
3
18 13 7
3
7
7
13 18
3
3
7
7
18 13 7
18 13 7
4

5. TRI PAR SÉLECTION
ALGORITHME RÉCURSIF
Tri_Selection (T: tableau, debut, fin : entier)
Debut
Si (debut < fin) alors
min rechercher_min(T, debut, fin)
Permuter (T, debut, min)
Tri_Selection (T, debut + 1, fin)
FSI
Fin
5

6. TRI PAR SÉLECTION
FONCTION « RECHERCHER_MIN »
Rechercher_min (T: tableau, debut, fin : entier): entier
Debut
min debut
Pour idebut +1 à fin faire
Si (T[i] < T[min]) alors min  i;
Rechercher_min  min;
Fin
6

7. TRI PAR SÉLECTION
COMPLEXITÉ DE LA FONCTION « RECHERCHER_MIN »
Rechercher_min (T: tableau, debut, fin : entier): entier
Debut
min debut
C1
Pour idebut +1 à fin faire
Si (T[i] < T[min]) alors min  i;
Nombre d’itération =
Fin – debut = n-1
Rechercher_min  min; C3
Fin
Tmin (n) = C1 + C2 (n-1) + C3 = C’ n + C’’  O(Tmin) = O (n)
7

8. TRI PAR SÉLECTION
COMPLEXITÉ
Tri_Selection (T: tableau, debut, fin : entier)
T (n) tq n = fin – debut + 1
Debut
Si (debut < fin) alors
min rechercher_min(T, debut, fin)
Permuter (T, debut, min)
Tmin (n)
C1
Tri_Selection (T, debut + 1, fin)
T (n - 1)
FSI
Fin
T (n) = T(n-1) + Tmin (n) + C
O(T) = O (n2)
8

9. TRI PAR INSERTION
PRINCIPE

Le principe est d’ordonner les deux premiers éléments et
d’insérer le 3e élément de manière à ce que les 3 premiers
éléments soient triés, ensuite d’ insérer le 4e élément à sa
place et ainsi de suite. A la fin de la ie itération, les i
premiers éléments de T sont triés et rangés au début du
tableau T′
7
3
18 13 7
3
7
18 13 7
3
7
7
3
7
7
13 18
13 18
3
3
7
7
18 13 7
13 18 7
9

10. TRI PAR INSERTION
ALGORITHME RÉCURSIF
Tri_Insertion (T: tableau, n : entier)
Debut
Si (n>1) alors
Tri_Insertion(T,n-1);
Insérer (T, n) // insérer le nème élément à sa place dans le tableau T[1..n-1]
FSI
Fin
10

11. TRI PAR INSERTION
PROCÉDURE « INSÉRER »
Inserer (T: tableau, n : entier)
Debut
in-1
Tant que (i>0 et T[i]>T[i+1]) faire
DTQ
Permuter (i+1, i)
i i-1
FTQ
FSI
Fin
11

12. TRI PAR INSERTION
COMPLEXITÉ DE LA PROCÉDURE « INSÉRER »
Inserer (VAR T: tableau, n : entier)
Debut
in-1
Tant que (i>0 et T[i]>T[i+1]) faire
DTQ
Permuter (i+1, i)
i i-1
Pire des cas que le nème élément
contient la valeur la plus petite
et dans ce cas on doit parcourir
tous le tableau  Nombre
d’itération maximal = n
n-1
FTQ
FSI
Fin
12
Tinsérer (n) = C1 n + C2  O(Tinsérer) = O (n)

13. TRI PAR INSERTION
COMPLEXITÉ
Tri_Insertion (T: tableau, n : entier)
T (n) tq n taille du tableau
Debut
Si (n>1) alors
Tri_Insertion(T,n-1);
T (n - 1)
// insérer le n-ème élément dans le tableau T[1..n-1] :
Insérer (T, n)
Tinsérer (n )
FSI
Fin
13
T (n) = T(n-1) + Tinsérer (n )
O(T) = O (n2)

14. TRI PAR PROPAGATION
PRINCIPE

L'algorithme de tri par propagation (ou à bulles) consiste à
faire remonter progressivement les plus grands éléments d'un
tableau. Son principe est d’inverser deux éléments successifs
s'ils ne sont pas classés dans le bon ordre et de recommencer
jusqu'à ce qu’on ne peut plus permuter.
7
3
3
3
7
7
3
13 7
13 7
18
18
3
7
18 13 7
3
18 13 7
7
13 7
7
7
18
13 18
3
3
3
7
7
7
18 13 7
13 18 7
7
13 18
14

15. TRI PAR PROPAGATION
ALGORITHME RÉCURSIF
Tri_Propagation (T: tableau, n : entier)
Debut
Si non Trier (T, n) alors
DSI
Pour i 1 à n-1 faire
Si T[i] > T[i+1] alors permuter (T[i], T(i+1))
// La dernière case contient toujours l’élément le plus grand
Tri_Propagation (T, n-1)
FSI
Fin
15

16. TRI PAR PROPAGATION
FONCTION « TRIER »
Fonction Trier (T: tableau, n : entier) : Booléen;
Debut
Ok vrai; i 1;
Tant que (i <n et non OK) faire
DTQ
Si T[i]>T[i+1] alors okfaux
ii+1
FTQ
Trier  OK
Fin
16

17. TRI PAR PROPAGATION
COMPLEXITÉ DE LA FONCTION « TRIER »
Fonction Trier (T: tableau, n : entier) : Booléen;
Debut
Ok vrai; i 1;
Tant que (i <n et non OK) faire
DTQ
Si T[i]>T[i+1] alors okfaux
ii+1
Pire des cas que le tableau soit
trié et dans ce cas on parcourt
tous le tableau  Nombre
d’itération maximal = n
n-1
FTQ
Trier  OK
Fin
17
Ttrier (n) = C1 n + C2  O(Ttrier) = O (n)

18. TRI PAR PROPAGATION
COMPLEXITÉ
Tri_Propagation (T: tableau, n : entier)
Debut
T (n) tq n taille du tableau
Ttrier (n)
Si non Trier (T, n) alors
DSI
Pour i 1 à n-1 faire
Si T[i] > T[i+1] alors permuter (T[i], T(i+1))
n-1 fois
// La dernière case contient toujours l’élément le plus grand
Tri_Propagation (T, n-1)
T (n-1)
FSI
Fin
18
T (n) = T(n-1) + Ttrier (n) + c1(n-1) + c2
O(T) = O (n2)

19. TRI PAR FUSION
PRINCIPE

Le principe est de trier deux tableaux de taille N/2 et
ensuite de les fusionner de sorte à ce que le tableau final
soit trié.
7
7
3
3
7
18 13 7
18
3
3
18 13 7
13 7
13
7
7
7
7
13
13 18
19
3
7
7
10 13 18

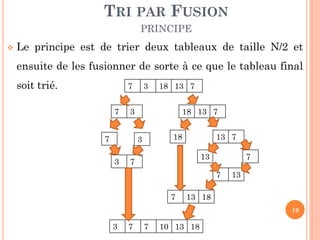
20. TRI PAR FUSION
PARADIGME DIVISER POUR RÉGNER

DIVISER: Diviser le tableau en deux tableaux:
T [debut..fin] = T1[debut..milieu] + T2[milieu+1..fin]

REGNER: trier (par fusion) les deux tableaux

COMBINER: combiner les 2 tableaux de telle manière
que le tableau T reste trie
20

21. TRI PAR FUSION
ALGORITHME RÉCURSIF
Tri_Fusion (T: tableau, debut, fin : entier)
Debut
Si (debut<fin) alors
milieu  (debut + fin) /2
Tri_Fusion(T, debut, milieu);
Tri_fusion (T, milieu + 1, fin);
Fusionner (T, debut, milieu, fin)
FSI
Fin
21

22. TRI PAR FUSION
PROCÉDURE « FUSIONNER »
Procédure fusionner(VAR T: tableau, debut, milieu, fin: entier)
Debut
Tmp: tableau temporaire du taille fin-debut+1
i debut; gauche  debut, droite  milieu + 1;
Tant que (i<=fin) faire
Si
((gauche<=milieu
et
T[gauche]<T[droite])
ou
droite>fin)
alors
Tmp[i]T[gauche]; gauche++;
Sinon
Tmp [i]T[droite]; droite++;
// recopier le tableau
Pour idebut à fin faire T[i]=tmp[i]
Fin
22

23. TRI PAR FUSION
COMPLEXITÉ DE LA PROCÉDURE « FUSIONNER »
Procédure fusionner(VAR T: tableau, debut, milieu, fin: entier)
Tfusionner(n) tq n= fin – debut +1
Debut
Tmp: tableau temporaire du taille fin-debut+1
i debut; gauche  debut, droite  milieu + 1;
Tant que (i<=fin) faire
Si
((gauche<=milieu
n fois
et
T[gauche]<T[droite])
ou
droite>fin)
alors
Tmp[i]T[gauche]; gauche++;
Sinon
Tmp [i]T[droite]; droite++;
// recopier le tableau
Pour idebut à fin faire T[i]=tmp[i]
Fin
n fois
Tfusionner(n) = c1 * n + c2  O (Tfusionner) = O (n)
23

24. TRI PAR FUSION
COMPLEXITÉ
Tri_Fusion (T: tableau, debut, fin : entier)
T (n) tq n taille du tableau
Debut
Si (debut<fin) alors
milieu  (debut + fin) /2
Tri_Fusion(T, debut, milieu);
T (n/2)
Tri_fusion (T, milieu + 1, fin);
T (n/2)
Fusionner (T, debut, milieu, fin)
Tfusionner(n)
FSI
Fin
24
T (n) = 2T(n/2) + Tfusionner(n)
O(T) = O (n log2 n)

25. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE IV:
ALGORITHMES DE TRI
Cours n°8: 3 Novembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

26. TRI RAPIDE
PRINCIPE

Le principe est de choisir une valeur dans le tableau appelée
pivot (par exemple la première valeur du tableau) et de
déplacer avant elle toutes celles qui lui sont inférieures et
après elle toutes celles qui lui sont supérieures. Réitérer le
procédé avec la tranche de tableau inférieure et la tranche de
tableau supérieure à ce pivot.
26

27. TRI RAPIDE
PARADIGME DIVISER POUR RÉGNER

DIVISER: Diviser le tableau en deux tableaux selon le
pivot choisi : T1[debut..pivot] et T2[pivot+1..fin]

REGNER: trier (par trie rapide) les deux tableaux

COMBINER: combiner les 2 tableaux:
T [debut..fin] = T1[debut..pivot] + T2[pivot+1..fin] est trié
27

28. TRI RAPIDE
ALGORITHME RÉCURSIF
Tri_Rapide (T: tableau, debut, fin : entier)
Debut
SI debut < fin alors
Pivotpartitionner(T, debut, fin , pivot)
Tri_Rapide(T, debut, pivot)
Tri_Rapide(T, pivot+1, fin)
FSI
Fin
28

29. TRI RAPIDE
FONCTION « PARTITIONNER »
Partitionner (T: tableau, debut, fin, pivot: entier): entier
Debut
permuter (T[pivot], T[fin])
j premier
Pour i 1 à fin -1 faire
SI T[i] <= T[fin] alors
Permuter (T[i], T[j])
jj+1
FSI
FP
Permuter (T[fin] , T[j])
Partitionner  j
Fin
29

30. TRI RAPIDE
FONCTION « PARTITIONNER »
Partitionner (T: tableau, debut, fin, pivot: entier): entier
Debut
permuter (T[pivot], T[fin])
j premier
Pour i 1 à fin -1 faire
SI T[i] <= T[fin] alors
Permuter (T[i], T[j])
jj+1
FSI
FP
Permuter (T[fin] , T[j])
Partitionner  j
Fin
30

31. TRI RAPIDE
COMPLEXITÉ DE LA FONCTION « PARTITIONNER »
Partitionner (T: tableau, debut, fin, pivot: entier): entier
Debut
permuter (T[pivot], T[fin])
Tpartitionner(n) tq n= fin – debut +1
j premier
Pour i 1 à fin -1 faire
Pire de cas: n-1 fois
SI T[i] <= T[fin] alors
Permuter (T[i], T[j])
jj+1
FSI
FP
Permuter (T[fin] , T[j])
Partitionner  j
Fin
Tpartitionner(n) = c1 * n + c2  O(Tpartitionner) = O (n)
31

32. TRI RAPIDE
COMPLEXITÉ
Tri_Rapide (T: tableau, debut, fin : entier)
T(n)/ n= fin – debut +1
Debut
SI debut < fin alors
Pivotpartitionner(T, debut, fin , pivot)
Tri_Rapide(T, debut, pivot)
Tri_Rapide(T, pivot+1, fin)
Tpartitionner(n)
T(pivot-debut+1)
T(fin-pivot)
FSI
Fin
32
T (n) = T(pivot-debut+1) + T(fin-pivot) + Tpartitionner(n)

33. TRI RAPIDE
CHOIX DU PIVOT ET COMPLEXITÉ
T (n) = T(pivot-debut+1) + T(fin-pivot) + Tpartitionner(n)

Cas 1: Pivot aléatoire. Le pire cas intervient quand le
partitionnement produit une région à n-1 éléments et une
région à un élément:
T(n) = T(n-1) + T(1) + Tpartitionner(n) = T(n-1) + f(n)
 O(T) = O(n2)

Cas 2: Pivot Arbitraire (premier élément, dernier
33
élément ou élément en milieu ). Même chose que le cas 1.

34. TRI RAPIDE
CHOIX DU PIVOT ET COMPLEXITÉ
T (n) = T(pivot-debut+1) + T(fin-pivot) + Tpartitionner(n)

Cas 3: Pivot optimal comme la valeur médiane qui
permet de couper le tableau en deux parties égales de
taille n/2 :
T(n) = 2T(n/2) + Tpartitionner(n)  O(T) = O(n log2 n)
34

35. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE IV:
ALGORITHMES DE TRI
Cours n°9: 10 Novembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

36. TRI PAR ABR
DÉFINITION

Un Arbre Binaire de Recherche (ABR) est un arbre
binaire, dans lequel chaque nœud contient un entier en
respectant la propriété suivante :

Inférieur (ou égal) aux entiers de son sous-arbre gauche

Supérieur strictement aux entiers de son sous-arbre droit
36

37. TRI PAR ABR
PRINCIPE
1. Insérer toutes les éléments du tableau dans un
ABR
20 15 10 35 19 13 5
3
12 7
16 40 25 38
20
15
35
25
10
40
19
5
3
13
7 12
38
16
37

38. TRI PAR ABR
PRINCIPE
2. Parcourir l’ABR en ordre infixé: fils gauche, nœud,
20
fils droit
15
35
25
10
40
19
5
3
3
5
7
13
7 12
38
16
10 12 13 15 16 19 20 25 35 38 40
38

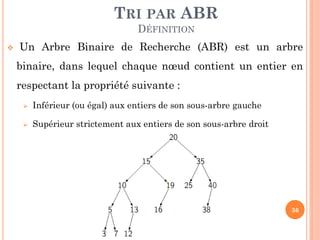
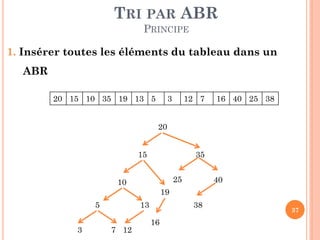
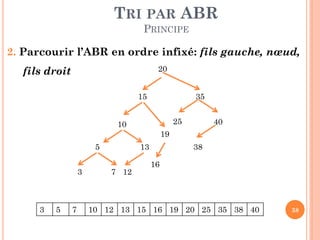
39. TRI PAR ABR
ALGORITHME ITÉRATIF
Soit AR un arbre de recherche binaire
Tri_ARB_IT (T: Tableau, n: entier)
Debut
// Construire ARB
ARNil
Pour i1 à n faire
ARInsérer (AR, T[i]).
Parcours_Infixe (AR, T); //Parcours Infixe
Fin
39

40. TRI PAR ABR
FONCTION « INSÉRER »
Insérer (AR: nœud , x: entier): nœud
Debut
SI (AR=Nil) alors // L’arbre est vide
AR Noeud(x,Nil,Nil) // Créer la racine (le premier nœud)
SINON
SI x ≤ valeur(AR) alors
AR.FGInsérer(x, FG(AR)) // Insérer à gauche
SINON
AR.FDInsérer(x, FD(AR)) // Insérer à droite
FSI
Insérer  AR
Fin
40

41. TRI PAR ABR
TERMINOLOGIE

Si h est la hauteur d’un arbre binaire de recherche, et n
le nombre des nœuds (ou la taille du tableau)
h=0
20
h=1
19
10
h=2
h=3
h=4
35
15
5
3
13
7 12
16
25
h=4
40
n = 14
38
41

42. TRI PAR ABR
COMPLEXITÉ DE LA FONCTION « INSÉRER »
Insérer (AR: nœud , x: entier): nœud
Tinsérer (h) tq h est la hauteur de l’arbre
Debut
SI (AR=Nil) alors // L’arbre est vide
AR Noeud(x,Nil,Nil) // Créer la racine (le premier nœud)
SINON
SI x ≤ valeur(AR) alors
AR.FGInsérer(x, FG(AR)) // Insérer à gauche Tinsérer (h +1)
SINON
AR.FDInsérer(x, FD(AR)) // Insérer à droite
Tinsérer (h +1)
FSI
Insérer  AR
Fin
42
Tinsérer (h+1) = Tinsérer (h) + c  O(Tinsérer ) = O (h)

43. TRI PAR ABR
COMPLEXITÉ DE LA FONCTION « INSÉRER »
O(Tinsérer) = O (h)

Pire de cas: un tableau déjà trié  Arbre mal
équilibré  h = n-1  O(Tinsérer) = O(n-1) = O(n)
h=0
25
h=1
18
25
15
5
2
15
h=2
h=3
h=4
18
5
2
43

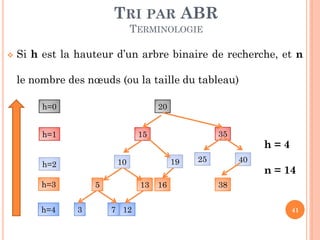
44. TRI PAR ABR
PARCOURS INFIXÉ
Soit « indice » une variable globale initialisé à 1
Parcours_Infixe (AR: nœud, T: Tableau)
Debut
Si ( AR  Nil) alors //Arbre n’est pas vide
Parcours_Infixe(FG(AR, T, indice))
T[indice]valeur (AR) //Écrire la valeur dans le tableau
Indice  indice + 1;
Parcours_Infixe(FD(AR), T, indice)
FSI
Fin
44

45. TRI PAR ABR
COMPLEXITÉ DU PARCOURS INFIXÉ
Soit « indice » une variable globale initialisé à 1
Parcours_Infixe (AR: nœud, T: Tableau)
Tinfixe (n) tq n le nombre des nœuds
Debut
Si ( AR  Nil) alors //Arbre n’est pas vide
Parcours_Infixe(FG(AR, T, indice))
Tinfixe (k)
T[indice]valeur (AR) //Écrire la valeur dans le tableau
Indice  indice + 1;
Parcours_Infixe(FD(AR), T, indice) Tinfixe (n-k-1)
FSI
Fin
45
Tinfixe (n) = Tinfixe (k) + Tinfixe (n-k-1) + c

46. TRI PAR ABR
COMPLEXITÉ DU PARCOURS INFIXÉ
Tinfixe (n) = Tinfixe (k) + Tinfixe (n-k-1) + c

Évidemment, le parcours infixé passe par tous les nœuds de l’arbre, ainsi
O(Tinfixe) = O(n)

Démonstration par récurrence

Cas évident n = 0, T(0) = 0  O(T) = O(0) = O (n) vérifiée

Hypothèse de récurrence pour k<n , on a O(T) = O (k)  T(k) = a k + b

Cas général:
Tinfixe (n) = Tinfixe (k) + Tinfixe (n-k-1) + c
Tinfixe (n) = a k + b + a (n-k-1) + b + c = a n + (2 b –a + c)
Tinfixe (n) = a n + d  O(Tinfixe) = O(n) ..........................CQFD
46

47. TRI PAR ABR
COMPLEXITÉ DE L’ALGORITHME ITÉRATIF
Soit AR un arbre de recherche binaire
Tri_ARB_IT (T: Tableau, n: entier)
TARB (n)
Debut
// Construire ARB
O(TARB)= n * O (n) + O (n)
= O (n2) + O(n)
ARNil
Pour i1 à n faire
n fois
= O(n2)
ARInsérer (AR, T[i]). Tinsérer (n)
Parcours_Infixe (AR, T); //Parcours Infixe Tinfixe (n)
Fin
47

48. TRI PAR ABR
ALGORITHME
RÉCURSIF
Tri_ABR(T: Tableau, n: entier, AR: nœud)
Debut
SI (n>0) alors
Insérer (ARB, T[n])
Tri_ABR(T, n-1, AR)
SINON // n=0 l’arbre est construit en totalité
Parcours_Infixe (AR, T);
FSI
Fin
48

49. TRI PAR ABR
COMPLEXITÉ DE L’ALGORITHME RÉCURSIF
Tri_ABR(T: Tableau, n: entier, AR: nœud)
TARB (n)
Debut
SI (n>0) alors
Insérer (ARB, T[n])
Tri_ABR(T, n-1, AR)
Tinsérer (n)
TARB (n-1)
SINON // n=0 l’arbre est construit en totalité
Parcours_Infixe (AR, T); Tinfixe (n)
FSI
Fin
49
TARB (n)= TARB (n – 1 ) + Tinsérer (n)  O (TARB ) = O(n2)

50. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE IV:
ALGORITHMES DE TRI
Cours n°10: 17 Novembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

51. TRI PAR TAS
DÉFINITION

Un TAS un arbre binaire qui vérifie les deux propriétés
suivantes :

Propriété structurelle: arbre binaire complet (ou
parfait), i.e. Tous les niveaux sont totalement remplis
sauf le dernier qui est rempli de la gauche vers la
droite.

Propriété d’ordre :

TASmin: valeur (père)  valeur (fils)

TASmax: valeur (père)  valeur (fils)
51

52. TRI PAR TAS
TASMIN
4
Minimum
5
6
15
16
9
25
14
7
12
11
20
8
Maximum
52

53. TRI PAR TAS
TASMAX
40
Maximum
35
15
1
26
19
13
14
17
12
11
20
8
Maximum
53

54. TRI PAR TAS
HAUTEUR D’UN TAS

Théorème: Un tas de n nœud a une hauteur O(log2 n)

Démonstration

Soit h, la hauteur d’un tas de n nœud
h=0 ; n0 = 20
h=1 ; n1 = 21
h=2 ; n2 = 22
h=3 ; n3 = 23
54

55. TRI PAR TAS
HAUTEUR D’UN TAS

Théorème: Un tas de n nœud a une hauteur O(log2 n)

Démonstration

Soit h, la hauteur d’un tas de n nœud

Au niveau ih, ni=2i

Donc n = 20 + 21 + 22 + ....+ 2h-1 + c tel que , 0c<2h
n = 2h + c  2h h  log2 n  O(h) = O(log2 n).

Conséquence: Les opérations proportionnelle à h sont
O (log2 n)
55

56. REPRÉSENTATION PAR TABLEAU

Un tas se représente naturellement par un tableau:

Les sommets sont numérotés par un parcours en largeur, de
gauche à droite.

Le sommet « i » est rangé dans la case d’indice i du tableau.
1
2
5
15
8
3
6
5
4
4
6
7
9
7
20
9
16
25
14
12
11
8
1
2
3
4
5
6
7
8
9
10
11
12
13
4
5
6
15
9
7
20
16
25
14
12
11
8
56

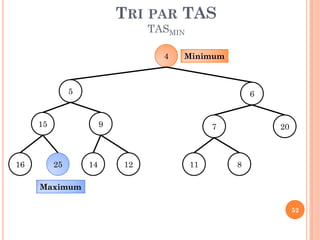
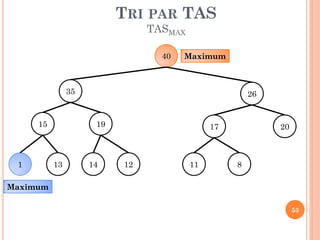
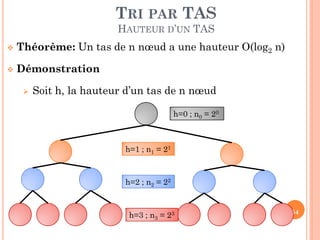
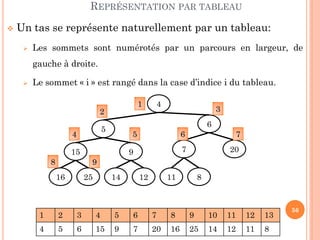
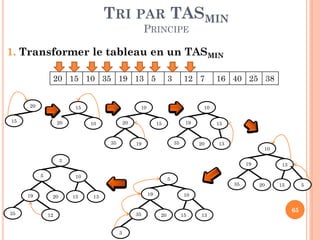
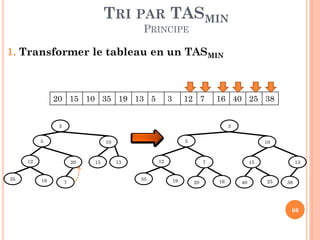
57. TRI PAR TAS
REPRÉSENTATION PAR TABLEAU

Indice(racine)=1

Indice(FG)=2*Indice(Père)

Indice(FD)=2*Indice(Père)+1

Indice(Père)= [Indice (Fils)/2]
1
2
3
4
5
6
7
8
9
10
11
12
13
4
5
6
15
9
7
20
16
25
14
12
11
8
57

58. TRI PAR TASMIN
INSERTION

Pour insérer une valeur « v » dans un TASmin
1.
Insérer « v » à la fin du dernier niveau de l’arbre (à la fin du
tableau).
2.
Tant que la valeur du père de « v » est plus grande que « v »,
échanger la valeur du père de v avec « v ».

Exemple: insertion de 3
4
6
5
15
16
4
25
5
7
9
6
14
15
12
9
7
20
11
20
16
8
25
58
14
12
11
8

59. 4
4
6
5
15
16
4
25
5
6
7
9
15
14
9
7
12
20
16
20
11
25
8
14
15
11
8
3
4
25
5
6
7
9
16
3
12
6
5
15
14
9
12
7
3
16
3
5
4
14
9
12
11
7
7
6
6
15
12
16
11
25
8
20
3
5
9
15
14
20
4
15
25
8
4
5
16
11
25
3
3
14
8
12
20
11
8
16
20
4
25
5
3
7
9
15
14
9
7
12
6
16
6
11
25
14
8
12
20
11
8
20

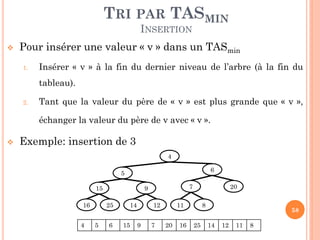
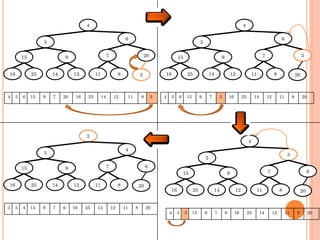
60. TRI PAR TASMIN
INSERTION
Procédure Insérer_TAS (Tas: tableau, n, x: entier)
Début
nn+1
in
Tas[i ]  x
Tant que (i/2 > 0 et Tas[i/2] > x) faire
Permuter (Tas, i, i/2)
i  i/2
60
Fin

61. TRI PAR TASMIN


1.
EXTRAIRE MINIMUM
Le minimum se trouve à la racine.
Pour supprimer la racine:
Remplacer la racine par le dernier élément « v » (à la fin du
tableau).
2.
Tant que la valeur « v » est supérieure à celle de l’un de ses fils,
échanger la valeur « v » avec celle du plus petit de ses fils.

Exemple :
4
6
5
15
16
4
25
5
7
9
6
14
15
12
9
7
11
20
16
20
61
26
25
14
12
11
8

62. 4
26
6
5
15
16
4
25
5
6
7
9
15
14
9
7
12
20
11
16
25
20
15
26
14
11
26
26
25
5
7
9
16
12
6
5
6
14
15
9
12
7
20
5
16
6
5
9
6
14
15
26
12
7
20
20
11
16
16
25
14
12
11
25
15
16
14
12
6
26
7
26
25
11
5
9
15
20
11
5
25
26
7
9
6
14
15
9
12
7
20
20
11
16
25
14
12
11 62

63. 5
5
6
9
15
16
25
5
7
26
9
6
14
15
12
26
7
20
20
11
16
15
16
25
14
12
6
26
11
5
25
26
7
9
6
14
15
9
12
7
20
20
11
16
25
14
12
11
5
6
9
15
16
5
25
9
7
26
6
14
15
12
26
7
20
20
11
16
25
14
26
11
63

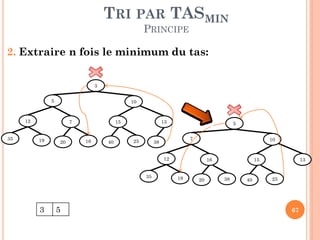
64. TRI PAR TASMIN
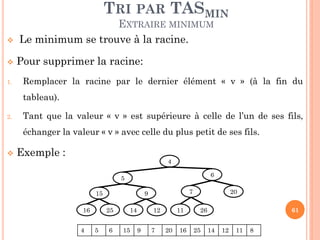
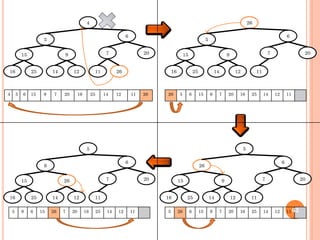
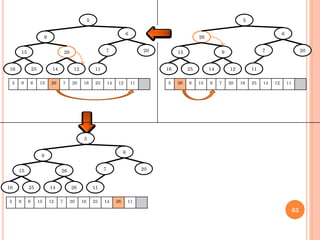
EXTRAIRE MINIMUM
ExtraireMin (Tas: tableau, n : entier )
Début
Tas [1]  T[n];
min  1; Sortie vrai
TQ (non sortie) faire
i min; g  2* i ; d  2 *i + 1
Si g < n et Tas[g] < Tas[min] alors min  g
Si d < n et Tas[d] < Tas[min] alors min  d
Si min  i alors Permuter (Tas, i, min)
Sinon Sortie vrai
Fin
64

65. TRI PAR TASMIN
PRINCIPE
1. Transformer le tableau en un TASMIN
20 15 10 35 19 13 5
20
15
15
20
3
12 7
10
10
20
10
35
16 40 25 38
19
15
35
19
15
20
13
10
3
5
19
35
19
10
20
15
5
19
13
35
12
3
35
13
20
15
5
10
20
15
13
65

66. TRI PAR TASMIN
PRINCIPE
1. Transformer le tableau en un TASMIN
20 15 10 35 19 13 5
3
12 7
16 40 25 38
3
3
5
12
35
20
19
5
10
7
15
10
12
13
35
7
19
20
15
16
40
13
25
38
66

67. TRI PAR TASMIN
PRINCIPE
2. Extraire n fois le minimum du tas:
3
5
10
12
35
7
19
20
15
16
40
13
25
5
7
38
10
12
35
3
5
16
19
20
15
38
40
13
25
67

68. TRI PAR TASMIN
PRINCIPE
2. Extraire n fois le minimum du tas:
7
12
10
19
16
15
13
10
35
25
38
20
40
12
13
19
35
3
5
7
10
16
25
20
15
40
38
68

69. TRI PAR TASMIN
PRINCIPE
2. Extraire n fois le minimum du tas:
13
12
16
19
35
16
13
20
15
19
40
20
35
25
15
38
40
25
38
15
16
19
25
20
38
40
35
69
3
5
7
10 12 13 15

70. TRI PAR TASMIN
PRINCIPE
2. Extraire n fois le minimum du tas:
16
19
35
19
20
25
20
38
40
35
38
25
35
40
38
25
35
40
38
20
35
40
38
25
40
38
40
40
3
5
7
10 12 13 15 16 19 20 25 35 38 40
70

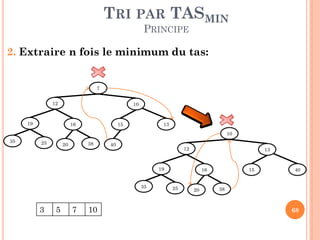
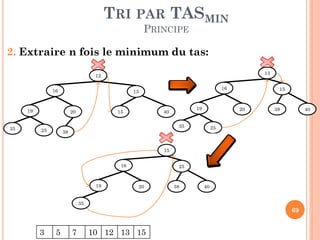
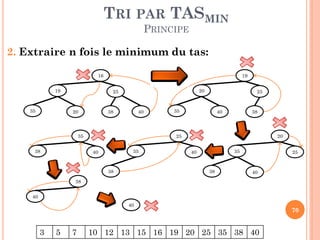
71. TRI PAR TASMIN
ALGORITHME ITÉRATIF
Tri_TASmin (T: Tableau, n: entier)
Début
//Construire le TAS
Pour i 1 à n faire
Insérer_TAS (Tas, i-1, T[i])
// Extraire les minimums
Pour i1 à n faire
T[i]  TAS[1]
Extraire_Minimum (TAS, n)
Fin
71

72. TRI PAR TASMIN
COMPLEXITÉ DE L’ALGORITHME ITÉRATIF
Tri_TASmin (T: Tableau, n: entier) TTAS (n) tq n la taille du tableau
Début
//Construire le TAS
Pour i 1 à n faire
Insérer_TAS (Tas, i-1, T[i])
TInsérer ??
// Extraire les minimums
Pour i0 à n-1 faire
T[i+1]  TAS[1]
Extraire_Minimum (TAS, n-i) Textraire??
Fin
72

73. TRI PAR TASMIN
COMPLEXITÉ DE LA PROCÉDURE INSÉRER_TAS
Procédure Insérer_TAS (Tas: tableau, n, x: entier)
TInsérer(n)
Début
nn+1
Pire des cas: le n+1 ème élément du
tableau est le minimum 
in
Tas[i ]  x
le nombre d’itération de la boucle
égale à log2(n+1)
Tant que (i/2 > 0 et Tas[i/2] > x) faire
Permuter (Tas, i, i/2)
i  i/2
73
Fin
TInsérer (n) = c1 log2(n+1) + c2  O(TInsérer ) = O(log2(n+1) )

74. TRI PAR TASMIN
COMPLEXITÉ DE LA PROCÉDURE EXTRAIRE_MINIMUM
Extraire_Minimum (Tas: tableau, n : entier ) TExtraire(n)
Début
Tas [1]  T[n];
min  1; Sortie vrai
TQ (non sortie) faire
i min; g  2* i ; d  2 *i + 1
Pire des cas: le dernier
élément est le maximum
 le nombre d’itération
Si g < n et Tas[g] < Tas[min] alors min  g correspond à la hauteur de
Si d < n et Tas[d] < Tas[min] alors min  d l’arbre donc égale à log2 n
Si min  i alors Permuter (Tas, i, min)
Sinon Sortie vrai
Fin
TExtraire (n) = c3 log2(n) + c4  O(TExtraire ) = O(log2(n) )
74

75. TRI PAR TASMIN
COMPLEXITÉ DE L’ALGORITHME ITÉRATIF
Tri_TASmin (T: Tableau, n: entier) TTAS (n) tq n la taille du tableau
Début
//Construire le TAS
Pour i 1 à n faire
Insérer_TAS (Tas, i-1, T[i])
TInsérer (i-1) = log2(i) + c2  log2(i)
// Extraire les minimums
Pour i0 à n-1 faire
T[i+1]  TAS[1]
Extraire_Minimum (TAS, n-i) Textraire (n-i) = log2(n-i) + c4  log2(n-i)
Fin
75
O(TTAS ) = O(nlog2(n) )

76. ALGORITHME RÉCURSIF
i1; phase1
Tri_TASmin (T, TAS: Tableau, n, i, phase: entier)
Début
Si Phase = 1 alors //Construire le TAS
Si (i<=n) alors
Insérer_TAS (Tas, i-1, T[i])
Tri_TASmin (T, TAS, i++, n, phase)
Sinon
Tri_TASmin(T, TAS, 0, n, 2) // On passe à la phase 2
Sinon // Phase 2: Extraire les minimums
Si (i<n) alors
T[i+1]  TAS[1]
Extraire_Minimum (TAS, n-i)
Tri_TASmin (T, TAS, i++, n, phase)
Fsi
Fin
76

77. COMPLEXITÉ DE L’ALGORITHME RÉCURSIF
i1; phase1
Tri_TASmin (T, TAS: Tableau, n, i, phase: entier)
TTAS (m) tq m= n-i+1 la taille effective du tableau (m n)
Début
Si Phase = 1 alors //Construire le TAS
Si (i<=n) alors
Insérer_TAS (Tas, i-1, T[i]) O(TInsérer ) = O(log2(n-m+1))
Tri_TASmin (T, TAS, i++, n, phase) TTAS (m-1)
Sinon
Tri_TASmin(T, TAS, 0, n, 2) // On passe à la phase 2
Sinon // Phase 2: Extraire les minimums
Si (i<n) alors
T[i+1]  TAS[1]
Extraire_Minimum (TAS, n-i) O(Textraire) = O(log2(m-1))
Tri_TASmin (T, TAS, i++, n, phase) TTAS (m-1)
Fsi
Fin
O(TTAS ) = O(nlog2(n) )
77

78. CONCLUSION
Algorithme de Tri
Complexité au Pire
Tri par Sélection
O(n2)
Tri par Insertion
O(n2)
Tri par Propagation
O(n2)
Tri par ABR
O(n2)
Tri Rapide
O(n2)
O(nlog2(n))
Tri par Fusion
O(nlog2(n))
Tri par TAS
O(nlog2(n))
78

79. EXERCICE

Réécrire
les
algorithmes
de
tri
(vus
précédemment) afin de pouvoir trier le tableau
en ordre décroissant (plus grand au plus petit).
79

80. TP: TRI PAR ABRE

Un Arbre Binaire de Recherche Équilibré (ABRE), comme son nom
indique, est un arbre :

binaire de recherche : chaque nœud possède au plus deux fils
(gauche et droit), et la valeur du père est inférieur ou égale à la valeur
de son fils gauche et supérieur strictement à la valeur de son fils droit.

Équilibré : possède un critère d'équilibre spécifique par exemple :

Dans TAS, l'arbre est complet, i.e. si sa hauteur est h, les niveaux
inférieurs (0, 1, 2,...., h-1) sont entièrement remplis.

Dans un arbre AVL, les hauteurs du sous arbre gauche et celle du
sous arbre droit diffèrent au plus de un.

Dans un arbre rouge-noir, la hauteur maximum est égale à 2 log2 (n
+ 1) où n est le nombre de nœuds.

.............
80

81. TP: TRI PAR ABRE

Le but de ce TP est de proposer un algorithme de tri par un ABRE
permettant de classer les éléments du tableau.

Pour ce faire, les étapes suivantes doivent être respectées :
1.
Conception de l’algorithme : définir la structure de l’ABRE choisi,
décrire le principe du tri, dérouler le principe sur un exemple, écrire
l’algorithme (version itérative et récursive) et enfin calculer
la
complexité de l’algorithme.
2.
Implémentation de l’algorithme : Développer une application sous
Java permettant, entre autre, de:

Via une interface graphique :

Saisir manuellement le tableau (la taille et les éléments), ou

Importer le tableau à partir d’un benchmark (fichier .txt)

Afficher le tableau trié

Calculer le temps d’exécution.
81

82. TP: TRI PAR ABRE

Pour ce faire, les étapes suivantes doivent être respectées :
1.
Conception de l’algorithme
2.
Implémentation de l’algorithme
3.
Test : Donner le temps d’exécution dans le cas où n=10, n=100,
n=1000 (n présente la taille du tableau).

Le
rapport
(au
maximum
sur
10
pages)
et
l’application (code source + exécutable .Jar sur un
CD-ROM) doivent être rendus un mois après la date
de remise du TP.
82

83. SOURCES DE CE COURS

Frédéric Vivien, Algorithmique avancée, École Normale Supérieure de Lyon, 2002.,
pp. 93. Disponible sur http://perso.ens-lyon.fr/frederic.vivien/Enseignement/Algo2001-2002/Cours.pdf

Slim
Msfar,
Algorithmique
et
Complexité,
2012,
pp
104.
Disponible
sur
http://p835.phpnet.org/testremorque/upload/catalogue/coursalgorithmi.pdf

Algorithmes
récursifs
de
tri,
disponible
sur
http://foofish.blogspot.com/2007/01/algorithmes-rcursifs-de-tri.html

François Laroussinie Algorithmes de tri, Université Paris Diderot (Paris 7), 2010, pp
110. Disponible sur www.liafa.jussieu.fr/~francoisl/IREM/tri.pdf‎

Parcours
d’un
arbre
binaire,
disponible
sur
math.univ-
lyon1.fr/irem/IMG/pdf/parcours_arbre_avec_solutions-2.pdf

Olivier
Bournez,
Cours
7:
Arbres
de
recherche.
Tas.
Disponible
sur
http://www.enseignement.polytechnique.fr/informatique/INF421/Amphi-b/cours7handout2x2.pdf

Renaud Dumont, Algorithmique P2, HeapSort et files de priorité, 2010, pp 83
31,
Disponible sur www.montefiore.ulg.ac.be/~dumont/pdf/ac7.pdf‎