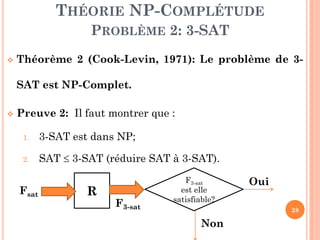
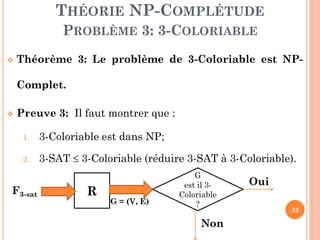
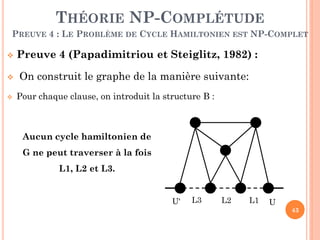
Le document traite de la théorie de la NP-complétude dans le cadre de l'algorithmique, en présentant les problèmes de décision et leur classification en classes P et NP. Il explique la notion de réduction entre problèmes, ainsi que les difficultés associées à la question ouverte de savoir si P est égal à NP. Plusieurs exemples de problèmes NP-complets, tels que SAT, 3-SAT et 3-coloriabilité, illustrent la théorie tout en notant l'importance de ces problèmes en informatique théorique.

1. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE VI:
NP-COMPLÉTUDE
AROUSSI
2013-2014
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. PLAN DU CHAPITRE VI
 Introduction
(Vocabulaire Général)
 Classification
 Notion
de Réduction
 Théorie
de NP-Complétude
 Quelques

de Problème
Problèmes NP-Complets
Conclusion
2

3. INTRODUCTION
PROBLÈME DE DÉCISION

Pour des raisons de simplicité et techniques, la théorie de
la NP-Complétude se limite à l’étude des problèmes de
décision dont la solution est formulée en termes
oui/non.

Un problème de décision est une paire P =(X,Y), où

X est l’ensemble des instances de P ;

Y est l’ensemble des instances-«oui»

X Y est l’ensemble des instances-«non»
3

4. INTRODUCTION
PROBLÈME DE DÉCISION

Un algorithme pour un problème de décision (X,Y) est un
algorithme qui calcule la fonction F : X →{0, 1}, définie
par

Cette restriction aux problèmes de décision est justifiée
par le fait que les autres problèmes qui ne sont pas de
décision, comme les problèmes d’optimisation et de
recherche, peuvent être facilement transformés en un
problème de décision équivalent.
4

5. INTRODUCTION
PROBLÈME DE DÉCISION VS AUTRES PROBLÈMES

Problème de Recherche:
Exemple
Entrée
Réponse
Algorithme de recherche
(Trouver un arbre recouvrant)
G (X, E) non
orienté
Arbre recouvrant
Algorithme de décision
(Existence d’un arbre recouvrant)
G (X, E) non
orienté
Oui/Non
Réduction de la recherche à la décision par test
d'hypothèse (La connexité de G)
5

6. INTRODUCTION
PROBLÈME DE DÉCISION VS AUTRES PROBLÈMES

Problème d’Optimisation:
Exemple
Entrée
Réponse
Algorithme d’optimisation
(Trouver un arbre recouvrant de poids
minimum)
G (X, E, W)
non orienté
Arbre
recouvrant
minimum
Algorithme de décision
(Existence d’un arbre recouvrant de poids
 k)
G (X, E, W)
non orienté
Oui/Non
Lorsque le critère d'optimisation est borné a priori,
réduction de l'optimisation à la décision par test
d'hypothèse (La connexité de G et le poids de l’arbre
recouvrant).
6

7. INTRODUCTION
ALGORITHME DÉTERMINISTE VS NON-DÉTERMINISTE

Un algorithme déterministe est un algorithme dont la
solution qu’il produit peut être déduite des spécifications
de l’algorithme lui-même.

Un algorithme non déterministe est un algorithme dont
la solution est devinée puis vérifiée.
7

8. INTRODUCTION
ALGORITHME EFFICACE

Pour différentes raisons, la convention suivante s’est
imposée en informatique :
Un algorithme est efficace (ou facile) si sa complexité en
temps est polynomiale, c’est-à-dire en O(nk) pour un entier
k.

Un problème est de complexité polynomiale s'il existe un
algorithme de complexité polynomiale le résolvant.
8

9. CLASSIFICATION DES PROBLÈMES
CLASSE P

La classe P regroupe tous les problèmes de décision qui
peuvent être résolus par un algorithme déterministe de
complexité polynomiale.

Exemple:

Problème de l’existence de l’arbre de recouvrement de poids  k
(Algorithme de Kruskal)

9
Problème de l’existence d’un chemin de longueur  k (Algorithme
de Dijkstra)

10. CLASSIFICATION DES PROBLÈMES
CLASSE NP

La classe NP (Non deterministic Polynomial) regroupe
tous les problèmes de décision qui peuvent être résolus
par un algorithme non-déterministe de complexité
polynomiale (i.e. dont la solution peut être vérifiée en
temps polynomial)

Pour montrer qu’un problème est dans la classe
NP, il suffit de trouver un algorithme qui vérifie si une sol
ution donnée est valide en temps polynomiale.
10

11. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 1: Problème de Satisfaction en calcul
propositionnel (SAT)

Soit F = (x1, ...., xn) une formule du calcul propositionnel
en Forme Normale Conjonctive, i.e. F = C1  C2  .....  Cm
pour une collection de clauses {C1, C2, ....., Cm} sur l’
ensemble X = {x1, ...., xn } de variables booléennes
(littéraux).

Décider si F est satisfiable, c-à-d décider s’il existe x1, ....,
xn  {0, 1}n tel que F s’évalue en vraie pour cette valeur 11
de
ses variables (toutes les clauses de C soient vraies).

12. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 2: Problème de K-SAT (k>2)

Soit F = (x1, ...., xn) une formule du calcul propositionnel
en Forme Normale Conjonctive, i.e. F = C1  C2  .....  Cm
pour une collection de clauses {C1, C2, ....., Cm} sur
l’ensemble X = {x1, ...., xn } tel que chaque clause
contient exactement k littéraux |Ci| = k.

Décider si F est satisfiable, c-à-d décider s’il existe x1, ....,
xn  {0, 1}n tel que F s’évalue en vraie pour cette valeur de
ses variables (toutes les clauses de C soient vraies).
12

13. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 3: Problème de sac à dos entier

Soient un ensemble d’objets avec un poids Pi et une
valeur Vi, une capacité de sac à dos Pmax et un objectif de
valeur Vmax.

Déterminer s’il existe un ensemble d’objets dont le poids
total  Pmax et la valeur totale  Vmax.
13

14. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 4: Problème du cycle hamiltonien

Soit G = (X, E) un graphe non orienté

Déterminer s’il existe un cycle hamiltonien, c’est-à-dire décider
s’il existe un chaîne de G passant une fois et une seule par
chacun des sommet et revenant à son point de départ.

Variantes:
chaîne
hamiltonien,
hamiltonien, chemin hamiltonienne.
circuit
14

15. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 5: Problème de voyageur de commerce
(PVC)

Un représentant doit visiter n villes. Il souhaite faire une tournée
en visitant chaque ville exactement une fois et en terminant sa
tournée dans la ville de départ.

Le voyage entre la ville i et la ville j a un coût c (i, j), et le
représentant souhaite effectuer une tournée dont le coût total est
15
minimum.

16. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 5: Problème de voyageur de commerce
(PVC)

Le problème de décision correspondant est:

Soit un graphe G= (V, E, C) non orienté.

Décider s’il existe une tournée de coût  k.
16

17. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 6: Problème de Coloriage de Graphe

Étant donnée le graphe G = (X, E) non orienté,
déterminer le nombre minimal de couleurs pour
colorier les sommets X du G tel que deux sommets
adjacent soient de couleur différente.
17

18. CLASSIFICATION DES PROBLÈMES
CLASSE NP

Problème 6: Problème de Coloriage de Graphe

Le problème de décision correspondant est:

Soient un graphe G = (X, E) et un entier k

Déterminer si le graphe G admet un coloriage avec au
moins de k couleurs.

Ce problème de décision est connu sous le nom du
18
problème K-Coloriabilité

19. CLASSIFICATION DES PROBLÈMES
COMPARAISON ENTRE LES DEUX CLASSES P ET NP

Clairement, P  NP mais la question qui se pose est :
P = NP ?

C’est l’une des questions (voire la question) non résolue les
plus célèbres qui défie les chercheurs depuis plus de 40 ans :
elle a été placée parmi la liste des sept problèmes du prix du
millénaire réputés insurmontables posés par le l’institut Clay
Mathematical en 2000. L’institut offre un million de dollars
à qui déterminerait la réponse à cette question.
19

20. CLASSIFICATION DES PROBLÈMES
COMPARAISON ENTRE LES DEUX CLASSES P ET NP

Clairement, P  NP mais la question qui se pose est :
P = NP ?

Intérêt: Si P = NP, alors tous les problèmes vérifiables
polynomialement seraient décidables en temps polynomial.

La plupart des personnes pensent que ces deux classes sont
distinctes car il y a un très grand nombre de problèmes pour
lesquels on n’arrive pas à produire d’algorithme polynomiaux
depuis plus de 40 ans.
20

21. NOTION DE RÉDUCTION
IDÉE

Soient A et B deux problèmes. Si A se réduit à B (noté A
 B) , alors

le problème A est plus facile que le problème B, ou

le problème B est plus difficile que le problème A.
21

22. NOTION DE RÉDUCTION
DÉFINITION

Soient A (XA, YA) et B (XB, YB) deux problèmes de
décision. Une réduction de A vers B (A  B) est une
fonction R : XA  XB calculable en temps polynomial telle
que
aYA ssi R(a) YB :
R
22

23. NOTION DE RÉDUCTION
PROPRIÉTÉS

Soient A (XA, YA), B (XB, YB) et C (XC, YC) des problèmes
de décision.

AA

A  B et B  C impliquent A  C.

A  B
et B  A
impliquent A  B (A et B sont
équivalents).
23

24. NOTION DE RÉDUCTION
APPLICATION À LA COMPARAISON DE DIFFICULTÉ

Intuitivement, si un problème est plus facile qu’un
problème polynomial, alors il est polynomial.

Formellement :

Si A  B, et si B  P alors A  P.

Si A  B, et si A  P alors B  P.
24

25. THÉORIE NP-COMPLÉTUDE
DÉFINITION

Un problème B est dit NP-complet, si
1.
2.

B  NP
 A  NP, A  B.
Les problèmes NP-complets sont donc les plus difficiles de
la classe NP.
25

26. THÉORIE NP-COMPLÉTUDE
PREUVE

Pour prouver la NP-complétude d’un problème B, il suffit
de prouver que :
1.
B est dans NP;
2.
A  B pour un problème A que l’on sait déjà NPcomplet.

La difficulté est d’arriver à en produire un premier
26
problème NP-Complet.

27. THÉORIE NP-COMPLÉTUDE
PROBLÈME 1: SAT

Théorème 1 (Cook-Levin, 1971): Le problème SAT est
NP-complet.

Le problème SAT est le premier problème montré comme
NP-complet.

Résultat admis: la preuve consiste en un codage d'une
machine de Turing qui vérifie les solutions de P en temps
polynomial.

Ce théorème va être utilisé pour en montrer par réduction
d’autres problèmes NP-Complet.
27

28. THÉORIE NP-COMPLÉTUDE
PROBLÈME 2: 3-SAT

Théorème 2 (Cook-Levin, 1971): Le problème de 3SAT est NP-Complet.

Preuve 2: Il faut montrer que :
1.
3-SAT est dans NP;
2.
SAT  3-SAT (réduire SAT à 3-SAT).
Fsat
R
F3-sat
F3-sat
est elle
satisfiable?
Oui
28
Non

29. THÉORIE NP-COMPLÉTUDE
PREUVE 2 : LE PROBLÈME DE DE 3-SAT EST NP-COMPLET

Preuve 2: SAT  3-SAT (réduire SAT à 3-SAT).

Toute clause du problème SAT peut être remplacée de manière
équivalente par un ensemble de clauses 3-SAT qui contiennent
chacune exactement trois littéraux.
29

30. THÉORIE NP-COMPLÉTUDE
PREUVE 2 : LE PROBLÈME DE DE 3-SAT EST NP-COMPLET

Preuve 2: SAT  3-SAT (réduire SAT à 3-SAT).

Toute clause du problème SAT peut être remplacée de manière
équivalente par un ensemble de clauses 3-SAT qui contiennent
chacune exactement trois littéraux.
30

31. THÉORIE NP-COMPLÉTUDE
PREUVE 2 : LE PROBLÈME DE DE 3-SAT EST NP-COMPLET

Preuve 2: SAT  3-SAT (réduire SAT à 3-SAT).

La
satisfiabilité
des
clauses
Z’
est
donc
équivalente
à
la
satisfaisabilité de l’ensemble initiale Z.

La réduction est manifestement polynomiale ; on a donc bien prouvé
que SAT se réduisait à 3-SAT; ce dernier est donc bien NP-complet
31

32. THÉORIE NP-COMPLÉTUDE
PROBLÈME 3: 3-COLORIABLE

Théorème 3: Le problème de 3-Coloriable est NPComplet.

Preuve 3: Il faut montrer que :
1.
3-Coloriable est dans NP;
2.
3-SAT  3-Coloriable (réduire 3-SAT à 3-Coloriable).
F3-sat
R
G = (V, E)
G
est il 3Coloriable
?
Non
Oui
32

33. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME

DE
3-COLORIABLE EST NP-COMPLET
Preuve 3: 3-SAT  3-Coloriable.
On construit un graphe ayant 3 + 2 n + 5 m sommets tels que:

Les trois premiers sont notés VRAI, FAUX, NSP. Ces trois sommets
sont reliés deux à deux en triangle, de sorte qu’ils doivent être tous
trois
de
couleurs
différentes.
On
appellera
les
couleurs
correspondantes CVRAI(e.g. vert), CFAUX(e.g. rouge), CNSP (e.g. bleu)
NSP
VRAI
FAUX
33

34. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME

DE
3-COLORIABLE EST NP-COMPLET
Preuve 3: 3-SAT  3-Coloriable.
On construit un graphe ayant 3 + 2 n + 5 m sommets tels que:

On associe un sommet à chaque variable (Xi) et au complémentaire
de chaque variable (Not Xi). Pour assurer qu’une variable prenne la
valeur VRAI ou FAUX, pour chaque variable xi on construit un
triangle dont les sommets sont Xi, NOT Xi, et NSP.
NSP
Xi
NSP
Not
Xi
Xi
Not
Xi
34

35. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME

DE
3-COLORIABLE EST NP-COMPLET
Preuve 3: 3-SAT  3-Coloriable.
On construit un graphe ayant 3 + 2 n + 5 m sommets tels que:

Pour chaque clause {A, B, C}, on introduit le motif :
A
3
2
B
4
C

0
Ce motif sous graphe est 3-coloriable
VRAI
1
35

36. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME

DE
3-COLORIABLE EST NP-COMPLET
Preuve 3: 3-SAT  3-Coloriable.
On construit un graphe ayant 3 + 2 n + 5 m sommets tels que:

Ce motif est 3-coloriable
A
3
2
B
CVRAI ou CFAUX
A
CVRAI ou CFAUX C
4
VRAI
C
1
3
2
B
0
0
4
VRAI
1
36

37. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME

3-COLORIABLE EST NP-COMPLET
DE
Preuve 3: 3-SAT  3-Coloriable.
On construit un graphe ayant 3 + 2 n + 5 m sommets tels que:

Ce motif est 3-coloriable
A
3
2
CVRAI ou CFAUX
B
4
VRAI
C
CVRAI ou CFAUX
A
C
1
3
2
B
0
0
4
VRAI
1
37

38. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME
DE
3-COLORIABLE EST NP-COMPLET

Preuve 3: 3-SAT  3-Coloriable.

Considérons alors le graphe formé des trois sommets distingués, des
triangles formés sur les variables, et des motifs donnés. Si ce graphe
est 3-coloriable, alors en particulier tout sous-graphe est coloriable.

À partir d’une 3-coloration du graphe, on construit une affectation de
valeurs de vérité en mettant à 1 toutes les variables coloriées par
CVRAI.
Cette affectation est cohérente (une variable et son
complémentaire ont bien une valeur opposée) et au moins une
variable par clause est à 1.

Inversement, étant donné une affectation de valeurs de vérité, il est
38
aisé de déduire une 3-coloration du graphe.

39. THÉORIE NP-COMPLÉTUDE
PREUVE 3 : LE PROBLÈME
DE
3-COLORIABLE EST NP-COMPLET

Preuve 3: 3-SAT  3-Coloriable.

L’existence d’une 3-coloration du graphe est donc
équivalente à la satisfaisabilité de la formule initiale.

La réduction est manifestement polynomiale ; on a donc
bien prouvé que 3-SAT se réduisait à 3-COLORABILITE ;
ce dernier est donc bien NP-complet.
39

40. THÉORIE NP-COMPLÉTUDE
PROBLÈME 4: CYCLE HAMILTONIEN

Théorème 4 (Karp, 1972): Le problème de Cycle
Hamiltonien est NP-Complet.

Preuve 4: Il faut montrer que :
1.
Cycle Hamiltonien est dans NP;
2.
Plusieurs méthodes:
a.
3-SAT  Cycle Hamiltonien.
b.
3-SAT  Recouvrement de Sommets Cycle Hamiltonien
c.
40
3-SAT  Stable  Recouvrement de Sommets  Cycle
hamiltonien

41. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET

Preuve 4 (Papadimitriou et Steiglitz, 1982) :
3-SAT  Cycle Hamiltonien.
F3-sat
R
G = (V, E)
G
contient il
un C. H?
Oui
Non
41

42. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET

Preuve 4 (Papadimitriou et Steiglitz, 1982) :

On construit le graphe de la manière suivante:

Pour chaque variable, on introduit le sous graphe suivant:
X
Not X

Chaque nouvelle variable est liée à la précédente
X1
X2
Xn
42

43. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET



Preuve 4 (Papadimitriou et Steiglitz, 1982) :
On construit le graphe de la manière suivante:
Pour chaque clause, on introduit la structure B :
Aucun cycle hamiltonien de
G ne peut traverser à la fois
L1, L2 et L3.
U'
L3
L2
L1
U
43

44. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET



Preuve 4 (Papadimitriou et Steiglitz, 1982) :
On construit le graphe de la manière suivante:
Les clauses sont liées comme suit:
C1
X1
C2
X2
Cm
Xn
44

45. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET



Preuve 4 (Papadimitriou et Steiglitz, 1982) :
On construit le graphe de la manière suivante:
Les littéraux de chaque clause sont liés aux variables la structure A
suivante:
45

46. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET

Preuve 4 (Papadimitriou et Steiglitz, 1982) :

Par exemple, le graphe suivant présente ces clauses
C1
C2
A
A
A
C3
A
A
A
A
A
X1
A
46
X2
X3

47. THÉORIE NP-COMPLÉTUDE
PREUVE 4 : LE PROBLÈME DE CYCLE HAMILTONIEN EST NP-COMPLET

Preuve 4 (Papadimitriou et Steiglitz, 1982) :

Nous affirmons maintenant que G est hamiltonien si et seulement si
F3-sat est satisfaisable. Soit C un cycle hamiltonien. On définit un
assignement en fixant un littéral à vrai si et seulement si C contient
l’arête correspondante. D’après les propriétés des structures A et B,
chaque clause contient un littéral qui est vrai.

Inversement, tout assignement satisfaisant définit un ensemble
d’arêtes qui correspondent à des littéraux qui sont vrai. Comme
chaque clause contient un littéral qui est vrai, cet ensemble d’arêtes
peut être complété en un cycle hamiltonien de G.

Enfin, la réduction est trivialement polynomiale.
47

48. THÉORIE NP-COMPLÉTUDE
PROBLÈME 5: PVC

Théorème
5:
Le
problème
du
voyageur
de
Commerce (PVC) est NP-Complet.

Preuve 5: Il faut montrer que :
1.
2.

PVC est dans NP;
Cycle Hamiltonien  PVC.
Le problème PVC revient à trouver un cycle hamiltonien
48
C dont la somme des poids des arêtes soit minimum.

49. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6: SAC À DOS

Théorème 6: Le problème du sac à dos est NPComplet.

Preuve 6: Il faut montrer que :
1.
Sac à Dos est dans NP;
2.
3-SAT  Stable 
Recouvrement des sommets 
Somme de sous ensemble  Sac à dos
49

50. THÉORIE NP-COMPLÉTUDE
PREUVE 6 : LE PROBLÈME DE SAC À DOS EST NP-COMPLET

Preuve 6: 3-SAT  Stable 
Recouvrement des
sommets  Somme de sous ensemble  Sac à dos.

Théorème 6.1 (Karp, 1972): Le problème du stable est NP-
Complet.

Théorème 6.2 (Karp, 1972): Le problème du recouvrement des
sommets est NP-Complet.

Théorème 6.3 (Karp, 1972): Le problème de somme de sous
50
ensemble est NP-Complet.

51. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.1: STABLE

Soit un graphe non orienté G et un entier k. Le problème
consiste à décider s’il existe un ensemble d'au moins k
sommets, ne contenant aucune paire de sommets voisins.

On appelle un tel ensemble un stable ou un ensemble
indépendant de G.
51

52. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.1: STABLE

Théorème 6.1 (Karp, 1972): Le problème du stable
est NP-Complet.

Preuve 6.1: Il faut montrer que :
1.
Stable est dans NP;
2.
3-SAT  Stable.
F3-sat
R
G = (V, E)
G
contient il un
stable de
taille k?
Oui
52
Non

53. THÉORIE NP-COMPLÉTUDE
PREUVE 6.1 : LE PROBLÈME DE STABLE EST NP-COMPLET

Preuve 6.1: 3-SAT  Stable

On construit un graphe G avec 3m sommets (m le nombre
des clauses):

Pour chaque littéral xi, G possède une arête entre chaque
sommet associé à un littéral xi et chaque sommet associé
à un littéral not xi

Xi
Not
Xi
Ainsi, un stable de G correspond à une affectation de
valeurs de vérité à une partie des variables;
53

54. THÉORIE NP-COMPLÉTUDE
PREUVE 6.1 : LE PROBLÈME DE STABLE EST NP-COMPLET

Preuve 6.1: 3-SAT  Stable

On construit un graphe G avec 3m sommets (m le nombre
des clauses):

Pour chaque clause C = L1  L2  L3, on associe un
triangle.
L1
L3

Ainsi,
L2
un stable de G contient au plus un des trois
sommets associés à la clause C
54

55. THÉORIE NP-COMPLÉTUDE
PREUVE 6.1 : LE PROBLÈME DE STABLE EST NP-COMPLET

Preuve 6.1: 3-SAT  Stable

Par exemple, le graphe suivant présente ces clauses
X1
Not
X2
Not
X1
Not
X3
X2
Not
X3
Not
X1
X3
Not
X2
55

56. THÉORIE NP-COMPLÉTUDE
PREUVE 6.1 : LE PROBLÈME DE STABLE EST NP-COMPLET

Preuve 6.1: 3-SAT  Stable

Soit m le nombre de clauses dans F. On démontre que F
est satisfiable ssi G possède un stable de taille m.

En effet, si F est satisfiable, on considère une assignation
des variables satisfaisant F. Pour chaque clause C de F,
on choisit un littéral de C rendu vrai par l’assignation :
cela définit m sommets formant un stable de G.
56

57. THÉORIE NP-COMPLÉTUDE
PREUVE 6.1 : LE PROBLÈME DE STABLE EST NP-COMPLET

Preuve 6.1: 3-SAT  Stable

Réciproquement, si G a un stable de taille m, alors il a
nécessairement un sommet dans chaque triangle. Ce
sommet correspond à un littéral rendant la clause
associée vraie, et forme une assignation des variables
cohérente par construction des arêtes.

La réduction est clairement polynomiale.
57

58. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.2: RECOUVREMENT DES SOMMETS

Soit un graphe non orienté G et un entier k. Le problème
consiste à décider s’il existe un ensemble d'au plus k
sommets couvrants toutes les arêtes (au moins une des 2
extrémités est couverte).

Théorème
6.2
(Karp,
1972):
Le
problème
du
recouvrement des sommets est NP-Complet.
58

59. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.2: RECOUVREMENT DES SOMMETS

Preuve 6.2: Il faut montrer que :
1.
Stable est dans NP;
2.
Stable  Recouvrement des sommets.

Le problème recouvrement des sommets est équivalent
au problème stable par passage au complémentaire:
Si G = (V, E) admet un stable X de taille k alors V-X
59
est un couvrant de taille n-k de G.

60. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.3: SOMME DE SOUS ENSEMBLE

Soit un ensemble fini d'entiers E et un entier t. Le
problème consiste à décider s’il existe un sous ensemble
E’ E tel que

Théorème 6.2 (Karp, 1972): Le problème de somme
de sous ensemble est NP-Complet.
60

61. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.3: SOMME DE SOUS ENSEMBLE

Preuve 6.3: Il faut montrer que :
1.
Stable est dans NP;
2.
Recouvrement des sommets  Somme de sous ensemble.
Un graphe
G = (A, B)
R
Oui
Un ensemble
d’entier E et
un entier t
?
Non
61

62. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.3: SOMME DE SOUS ENSEMBLE

Preuve 6.3: Recouvrement des sommets  Somme
de sous ensemble.

Numéroter les sommets (A) entre 0 et n-1 et les arêtes (B) entre 0 et
m-1.

Soit D = (dij) la matrice d’incidence arête-sommet, c.-à-d.: que dij = 1
si l’arête i est incidente au sommet j, dij = 0 sinon.

Construire l'ensemble E à partir de G comme suit:

Pour chaque arête i est associé l'entier bi (b4)

Pour chaque sommet j est associé un poids aj tel que:
62

63. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.3: SOMME DE SOUS ENSEMBLE

Preuve 6.3: Recouvrement des sommets  Somme
de sous ensemble.

Construire l'ensemble E à partir de G comme suit:

Pour chaque arête i est associé l'entier bi (b4)

Pour chaque sommet j est associé un poids aj tel que:

On construit l'entier t :
63

64. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6.3: SOMME DE SOUS ENSEMBLE

Preuve 6.3: Recouvrement des sommets  Somme
de sous ensemble.
1.
Pour tout sous-ensemble E’ de somme t, il y a k termes
correspondant à des sommets dans E’.
2.
Inversement, étant donnée une couverture de sommets,
on construit l’ensemble E’ en prenant tout simplement
les sommets de la couverture.
3.
Il est facile de voir que la réduction s’effectue en temps
polynomial.
64

65. THÉORIE NP-COMPLÉTUDE
PROBLÈME 6: SAC À DOS

Théorème 6: Le problème du sac à dos est NPComplet.

Preuve 6: Il faut montrer que :
1.
Sac à Dos est dans NP;
2.
Somme de sous ensemble  Sac à dos

En particulier pour ai = pi et Pmax = Vmax = t, on trouve
65
problème de somme de sous ensemble.

66. SOURCES DE CE COURS

Olivier Bournez, Fondements de l’informatique Logique, modèles, et calculs,
Chapitre 12: Quelques problèmes NP-complets, Cours INF423 de l’Ecole
Polytechnique, 2013, pp. 234.

Jean Fonlupt et Alexandre Skoda. Optimisation combinatoire – Théorie et
algorithmes, Chapitre 15: NP-complétude, 2010, 664p.

Gilles Schaeffer, Cours 4: Réduction et NP-complétude, 2010, pp. 124,
Disponible
sur
http://www.enseignement.polytechnique.fr/informatique/INF550/Cours1011/
INF550-2010-5.pdf

Johanne Cohen, La NP-complétude, PRISM/CNRS, 2012, pp. 95, Disponible
66
sur http://www.prism.uvsq.fr/~joco/enseignement/Complexite.pdf