Le document présente un cours sur l'algorithmique avancée au sein du Master en Génie des Systèmes Informatiques de l'Université Blida 1, avec un accent sur les structures de données telles que les arbres de recherche. Il décrit les objectifs du cours, le contenu, les évaluations ainsi que les différentes notions fondamentales autour des arbres, y compris leurs définitions, typologies et méthodes de parcours. Les concepts et méthodes abordés incluent notamment les arbres binaires, les heuristiques et la notion de NP-complétude dans divers domaines d'application algorithmique.

1. ALGORITHMIQUE AVANCÉE
Université Blida 1
Faculté des Sciences
Département d’Informatique
Master GSI (Génie des Systèmes Informatiques)
Semestre 1
Mme AROUSSI
2015-2016
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. PRÉAMBULE
 Pré-requis: Cours (Algo1-S4, Algo 2-S5).
 UEF: GLOG (Génie Logiciel)
 Volume horaire hebdomadaire: 1.5H Cours + 1.5H TD
 Évaluation: continu + Examen
 Coefficient 1, Crédit 3
2

3. OBJECTIFS DU COURS
 Donner un panorama des structures et des méthodes
que nous retrouvons dans divers domaines
d'applications algorithmiques: codage, réseaux,
robotique, compilation, conception assistée par
ordinateur (CAO), etc...
 Savoir analyser et comparer les performances de
différentes solutions algorithmiques.
3

4. CONTENU DU COURS
I. Arbres de Recherche
II. Plus Courts Chemins
III. NP-Complétude
IV. Heuristiques & Méta-heuristiques
4

5. CHAPITRE I:
ARBRES DE RECHERCHE
Université Blida 1
Faculté des Sciences
Département d’Informatique
Master GSI (Génie des Systèmes Informatiques)
Semestre 1
Mme AROUSSI
2015-2016
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

6.  Introduction
 Définitions et Terminologies
 Topologie
 Partie I: Arbres Binaires
 Partie II: Arbres Binaires de Recherche (ABR)
 Partie III: Arbres AVL
 Partie IV: Arbres M-aire de Recherche (AMR)
 Partie V: B-Arbres
6
PLAN DU CHAPITRE I

7. 7
 Dans les tableaux, nous avons :
 Un accès direct par indice (rapide)
 L’insertion et la suppression nécessitent des décalages
 Dans les Listes Linéaires Chaînées, nous avons :
 Un accès séquentiel lent
 L’insertion et la suppression se font uniquement par modification de
chaînage
 Les arbres représentent un compromis entre les deux :
 Un accès relativement rapide à un élément à partir de sa clé
 L’insertion et la suppression non coûteuses
INTRODUCTION

8. 8
 De plus, les arbres sont des structures de données
fondamentales en informatique, très utilisés dans tous les
domaines, parce qu’ils sont bien adaptés à la
représentation naturelle d’informations homogènes
organisées, et d’une grande commodité et rapidité de
manipulation.
INTRODUCTION

9. 9
 Leur usage est multiple, car il capte l’idée de hiérarchie; à
titre d’exemples, nous pouvons citer:
 Découpage d’un livre en parties, chapitres, sections,
paragraphes…,
INTRODUCTION
Livre
C1 C2 C3
S1.1 S1.2 S2.1 S2.2 S2.3
S2.1.1 S2.1.2

10. 10
 Leur usage est multiple, car il capte l’idée de hiérarchie; à
titre d’exemples, nous pouvons citer:
 Hiérarchies de fichiers,
INTRODUCTION

11. 11
 Leur usage est multiple, car il capte l’idée de hiérarchie; à
titre d’exemples, nous pouvons citer:
 Expressions Arithmétiques
INTRODUCTION
-
A *
+ F
B *
C -
D E
 L’expression A - (B + C * (D - E)) * F
se représente facilement par un arbre
où apparaît clairement la priorité des
opérations:

12. 12
DÉFINITION & TERMINOLOGIES
 Un arbre est une structure de données (souvent dynamique)
représentant un ensemble de valeurs organisées
hiérarchiquement (non linéaire). Chaque valeur est stockée dans
un nœud. Les nœuds sont connectés entre eux par des arêtes
qui représentent des relations parent/fils.
A
C DB
E G HF I
LKJ
NœudsArêtes

13. 13
DÉFINITION & TERMINOLOGIES
 Racine: est le nœud qui n'a
pas de prédécesseur (parent) et
possède zéro ou plusieurs fils. La
racine constitue la caractéristique
d'un arbre.
 Feuille : est un nœud qui n'a
pas de successeur (fils). Une
feuille est aussi appelée un nœud
externe.
 Nœud interne : est tout nœud
qui admet au moins un
successeur (fils).
A
C DB
E G HF I
LKJ
Racine
Nœud interne
Feuilles

14. 14
DÉFINITION & TERMINOLOGIES
 Fils d’un nœud : sont ses
successeurs. Dans l'exemple, F,
G, H, et I sont les fils du nœud D.
 Frères : sont les successeurs
ou les fils issus d'un même nœud
(parent direct). Dans l'exemple,
B, C et D sont des frères.
 Père : est un nœud qui admet
au moins un successeur (fils).
Dans l'exemple, D est le père des
nœuds F, G, H et I.
A
C DB
E G HF I
LKJ

15. 15
DÉFINITION & TERMINOLOGIES
 Sous arbre : est une portion
de l'arbre. Dans l'exemple, le
nœud G avec ces deux fils J et K
constituent un sous arbre.
 Une branche est une suite de
nœuds connectés de père en fils
(de la racine à une feuille).
A-B-E
 A-C
 A-D-F
A-D-G-J
…..
A
C DB
E G HF I
LKJ

16. 16
DÉFINITION & TERMINOLOGIES
 Descendants d’un nœud :
sont tous les nœuds du sous arbre
de racine nœud. Dans l'exemple,
les descendants de D sont F, G,
H, I, J, K et L.
 Ascendants d’un nœud :
sont tous les nœuds se trouvant
sur la branche de la racine vers
ce nœud. Dans l'exemple, les
ascendants de J sont G, D et A.
Les ascendants de E sont B et A.
A
C DB
E G HF I
LKJ

17. 17
DÉFINITION & TERMINOLOGIES
 Taille d’un arbre: est le
nombre de nœuds qu’il possède.
 Taille de l’arbre ci contre = 12
 Un arbre vide est de taille
égale à 0.
Degré d’un nœud : est le
nombre de ses fils. Dans
l'exemple, le degré de B est 1, le
degré de D est 4.
 Ordre d’un arbre : est le
degré maximum de ses nœuds.
 Ordre de l’arbre ci contre = 4
A
C DB
E G HF I
LKJ

18. 18
DÉFINITION & TERMINOLOGIES
 Le niveau d'un nœud: est la distance qui le sépare de la
racine:
 Le niveau de la racine = 0
 Le niveau de chaque nœud est égale au niveau de son père plus 1
 Le niveau du nœud contenant ‘G' est égal à 2.
Racine
…..…………..…………………………………………….......
………………..…………………………………………….......
……………………………….......
.…………………………………………….......
A
C DB
E G HF I
LKJ
Niveaux
0
1
2
3

19. 19
DÉFINITION & TERMINOLOGIES
 La profondeur d'un arbre (ou sa hauteur) : est le plus
grand niveau, c-à-d la distance entre la racine et la feuille la plus
lointaine. Dans l'exemple, la profondeur de l'arbre est égal à 3
Racine
…..…………..…………………………………………….......
………………..…………………………………………….......
……………………………….......
.…………………………………………….......
A
C DB
E G HF I
LKJ
Niveaux
0
1
2
3

20. 20
DÉFINITION & TERMINOLOGIES
 Forêt : est un ensemble d'arbres.
A
C DB
E
G
HF I
L
KJ

21. 21
DÉFINITION & TERMINOLOGIES
Définition récursive
 Cas particulier: NIL est un arbre vide, contenant zéro nœud
T1
T’1
Racine
Racine de T1
Racine de T’1
 Cas général: SI n est un
nœud et si T1, T2, ...Tm sont
des arbres, ALORS on peut
construire un nouvel arbre en
connectant T1, T2, ...Tm
comme des fils à n.
 Chaque Ti est définit de la
même manière (récursivement).
 T1, T2, ...Tm sont alors des
sous- arbres de n.

22. 22
TYPOLOGIE
Arbre binaire : est un arbre où le degré maximum d’un nœud
est égal à 2.
Arbre de Recherche Binaire : est un arbre binaire où la clé
de chaque nœud est supérieure à celles de ses descendants
gauche, et inférieure à celles de ses descendants droits.
Arbre m-aire d’ordre n : est un arbre ou le degré maximum
d’un nœud est égal à n.
B-Arbre d’ordre n: est un arbre où :
 la racine a au moins 2 fils
 chaque nœud, autre que la racine, a entre n/2 et n fils
 tous les nœuds feuilles sont au même niveau
 ……

23. PARTIE II:
ARBRES BINAIRES

24.  Définition
 Modèle
 Parcours
 Exemples d’application
24
PLAN DE LA PARTIE II

25. 25
DÉFINITION
Un arbre binaire est un arbre où chaque nœud est connecté à
deux sous-arbres (un sous-arbre gauche et un sous-arbre droit).
Donc, un arbre binaire est un arbre d’ordre 2, c’est-à-dire que
chaque nœuds a au plus deux fils. Ainsi, le premier fils d'un nœud
n est appelé Fils-Gauche (FG) et le deuxième fils est appelé Fils-
Droit (FD). A
B
C KG
F
H I
J
racine
D
NIL

26. 26
DÉFINITION
 Un arbre binaire est dit strictement binaire si chaque nœud
interne (non feuille) a exactement 2 fils différents de NIL.
 Si un arbre strictement binaire a n feuilles Alors :
 le nombre total de ses nœuds = 2n-1.
 le nombre de ses nœuds non feuilles (nœuds internes) = n-1
A
B
C KG
F
H I
J
racine
D
M
 Le nombre de feuilles : n=6
(C, D,H, M, J, K)
 Le nombre total de nœuds :
2n-1=11
 Le nombre de nœuds
internes: n-1=5 (A, B, F, G, I)

27. 27
DÉFINITION
 Un arbre binaire complet est un arbre strictement binaire où
toutes les feuilles sont au même niveau.
 Dans un arbre binaire complet de profondeur « d » :
le nombre total de nœuds n = 20 + 21 + 22 + ... 2d = 2d+1-1
ainsi, d = log2(n+1) – 1
le nombre de nœuds internes = 2d-1
le nombre de feuilles = 2d
le nombre de nœuds dans le niveau i = 2i
racine
D
A
B
C KG
F

28. 28
DÉFINITION
 Un arbre binaire complet est un arbre strictement binaire où
toutes les feuilles sont au même niveau.
 Dans l’exemple ci dessous:
d = 2
le nombre total de nœuds n = 23-1 = 7
le nombre de nœuds internes = 22-1 = 3
le nombre de feuilles = 22 = 4
le nombre de nœuds dans le niveau 1 = 2
racine
D
A
B
C KG
F

29. 29
MODÈLE
 L'arbre est implémenté souvent de manière dynamique
comme un ensemble de maillons (nœuds) chaînés entre eux.
 La structure d'un nœud de l'arbre est la suivante :
Structure de Données
TYPE Tnoeud = STRUCTURE
Info : Typeqq
FG : * Tnoeud
FD : * Tnoeud
FIN
VAR Arbre : * Tnoeud

30. 30
MODÈLE
 On définit le modèle (machine abstraite) suivant d’un arbre
binaire:
Fonction Rôle
Info(p) permet d'accéder à l'information du nœud p
FG(p) permet d'accéder à l'information de fils gauche du nœud p
FD(p) permet d'accéder à l'information de fils droit du nœud p
Aff_info(p, x) permet de modifier l'information du nœud p
Aff_FG(p, x) permet de modifier l'information de fils gauche du nœud p
Aff_FD(p, x) permet de modifier l'information de fils droit du nœud p
Créer_noeud(x)
permet de créer un nœud avec x comme information et
retourne la référence du nœud. Le nœud créé a Nil comme fils
gauche et droit.
Liberer_noeud(p) permet de libérer le nœud référencé par p.

31. 31
PARCOURS
 Le parcours d’un arbre consiste à passer par tous ses
nœuds.
 Les parcours permettent d’effectuer tout un ensemble de
traitement sur les arbres.
 On distingue deux types de parcours :
 Des parcours en profondeur (depth-first) explorent
l'arbre branche par branche. Parmi lesquels: le Préordre,
l‘Inordre et le Postordre.
Des parcours en largeur (breadth-first) explorent
l'arbre niveau par niveau

32. 32
PARCOURS EN PROFONDEUR
 Dans un parcours en profondeur, on descend le plus
profondément possible dans l’arbre puis, une fois qu’une
feuille a été atteinte, on remonte pour explorer les autres
branches en commençant par la branche « la plus basse »
parmi celles non encore parcourues.
 Le parcours en profondeur peut se faire en :
Préordre (Préfixe) : où on affiche la racine avant ses fils (Racine
FG FD),
Inordre (Infixe) : où on affiche le fils gauche avant sa racine et
son frère droit (FG Racine FD),
 Postordre(Postfixe) : où on affiche les fils avant leur racine (FG
FD Racine).

33. 33
PARCOURS EN PROFONDEUR
 Ces parcours (préordre, inordre et postordre) sont des
parcours simples à définir et à programmer (en récursif).
 Soit R un arbre binaire (pouvant être vide : R=NIL).
 S'il n'est pas vide (n pointe le nœud racine), alors il a la forme
suivante (avec T1 et T2 des sous arbres définis de la même manière
que n) :
R
T1 T2
Sous arbre gauche G Sous arbre droit D

34. 34
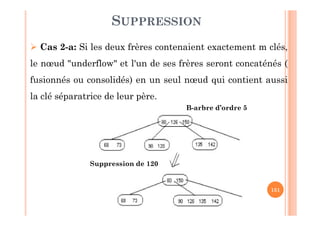
PARCOURS PREORDRE
 Le parcours préordre de R (s'il n'est pas vide) consiste à
visiter le nœud racine (R) ensuite parcourir récursivement
en préordre les sous arbres T1 (sous arbre gauche) puis T2
(sous arbre droit) ce qui donne : [ R , T1 , T2 ou RGD]
R
T1 T2
Sous arbre gauche G Sous arbre droit D

35. 35
PARCOURS PREORDRE
 Le parcours préordre de R (s'il n'est pas vide) consiste à
visiter le nœud racine (R) ensuite parcourir récursivement
en préordre les sous arbres T1 (sous arbre gauche) puis T2
(sous arbre droit) ce qui donne : [ R , T1 , T2 ou RGD]
A
B C
E GD F
H I
HID EB FGA CRésultat de parcours:

36. 36
PARCOURS PREORDRE
 La procédure (récursive) qui affiche les valeurs en
parcours préordre d’un arbre de racine R est :
Procédure Préordre( R:* Tnoeud )
Début
SI R ≠ NIL
ecrire( Info(R) )
Préordre( FG(R) )
Préordre( FD(R) )
FSI
fin

37. 37
PARCOURS INORDRE
 Le parcours inordre de R (s'il n'est pas vide) consiste
d'abord à parcourir récursivement en inordre le sous arbre
gauche T1, puis visiter le nœud racine (R) ensuite parcourir
récursivement en inordre le sous arbre droit T2 ce qui donne
[ T1 , R , T2 ou GRD ]
R
T1 T2
Sous arbre gauche G Sous arbre droit D

38. 38
PARCOURS INORDRE
 Le parcours inordre de R (s'il n'est pas vide) consiste
d'abord à parcourir récursivement en inordre le sous arbre
gauche T1, puis visiter le nœud racine (R) ensuite parcourir
récursivement en inordre le sous arbre droit T2 ce qui donne
[ T1 , R , T2 ou GRD ]
A
B C
E GD F
H I
Résultat de parcours: H ID EB F GA C

39. 39
PARCOURS INORDRE
 La procédure (récursive) qui affiche les valeurs en
parcours inordre d’un arbre de racine R est :
Procédure Inordre( R:*Tnoeud )
Début
SI R ≠ NIL
Inordre( FG(R) )
ecrire( Info(R) )
Inordre( FD(R) )
FSI
fin

40. 40
PARCOURS POSTORDRE
 Le parcours postordre de R (s'il n'est pas vide) consiste
d'abord à parcourir récursivement en postordre les sous
arbres T1 puis T2 ensuite visiter le nœud racine (R) ce qui
donne [ T1 , T2 , R ou GDR]
R
T1 T2
Sous arbre gauche G Sous arbre droit D

41. 41
PARCOURS POSTORDRE
 Le parcours postordre de R (s'il n'est pas vide) consiste
d'abord à parcourir récursivement en postordre les sous
arbres T1 puis T2 ensuite visiter le nœud racine (R) ce qui
donne [ T1 , T2 , R ou GDR]
A
B C
E GD F
H I
Résultat de parcours: HIDEBFG AC

42. 42
PARCOURS POSTORDRE
 La procédure (récursive) qui affiche les valeurs en
parcours postordre d’un arbre de racine R est :
Procédure Postordre( R: *Tnoeud)
Début
SI R≠NIL
Postordre( FG(R) )
Postordre( FD(R) )
ecrire( Info(R) )
FSI
fin

43. 43
PARCOURS EN PROFONDEUR
 On peut faire ces trois parcours sans utiliser la
récursivité. Il faudra alors un moyen pour pouvoir remonter
dans les branches de l'arbre:
 On pourra par exemple utiliser une structure de pile pour
sauvegarder les adresses des nœuds par lesquels on est descendu et
les dépiler quand on en aura besoin pour remonter.
 On peut aussi enrichir la structure des nœuds en incluant un
pointeur vers le nœud père.
 Il existe d'autres types de parcours en profondeur, comme
par exemple:
 Le préordre inverse (R T2 T1 ou RDG),
 L'inordre inverse (T2 R T1 ou DRG),
 Le postordre inverse (T2 T1 R ou DGR).

44. 44
PARCOURS EN LARGEUR
 Dans le parcours par niveau, tous les nœuds d’un même
niveau sont traités avant de descendre au niveau suivant
Résultat de parcours:A
B C
E GD F
H I
HIDEB FGA C

45. 45
PARCOURS EN LARGEUR
 Dans le parcours par niveau, tous les nœuds d’un même
niveau sont traités avant de descendre au niveau suivant
Procédure parcours_largeur( R:* Tnoeud )
Var F:filed’attente; P: *Tnoeud;
Debut
P←R;
Si R ≠ NIL Alors
Enfiler(F,P);
TQ (Non FileVide(F))
Defiler(F,P);
écrire(info(P));
Si FG(P) ≠ NIL Alors Enfiler(F,FG(P));
Si FD(P) ≠ NIL Alors Enfiler(F,FD(P));
FTQ
Fin

46. 46
EXEMPLES D’APPLICATION
 Représentation des Expressions Arithmétiques :
 Les expressions arithmétiques peuvent êtres représentées sous
forme d'arbre binaire. Les nœuds internes contiennent des
opérateurs, alors que les feuilles contiennent des valeurs
(opérandes).
 Exemple: l'expression (a-b)*((c+d)/e) sera représentée par l'arbre
suivant :
c
e
*
- /
+
d
ba

47. 47
EXEMPLES D’APPLICATION
 Représentation des Expressions Arithmétiques :
 Les différentes formes de représentation d’une expression
arithmétiques peuvent être trouvés en parcourant l’arbre:
 Le parcours en préordre (RGD) donne la forme polonaise préfixée,
 Le postordre (GDR) donne la forme postfixée
 Le parcours inordre (GRD) donne la forme infixée (forme normale
sans parenthèses)
c
e
*
- /
+
d
ba

48. 48
EXEMPLES D’APPLICATION
 Représentation des Expressions Arithmétiques :
 L’évaluation d’une expression arithmétiques peuvent se faire les
deux fonctions suivantes:
 La fonction Opérande(T) qui retourne vrai si T est un
opérande, sinon elle retourne faux.
 La fonction Calcul qui permet de calculer l’opération
arithmétique entre deux opérandes

49. 49
EXEMPLES D’APPLICATION
 Représentation des Expressions Arithmétiques :
c
e
*
- /
+
d
ba
Fonction Eval_inordre(A: *Tnoeud): réel
SI (A= Null) alors
Retourner (0)
SINON
SI Operande(A) alors
Retourner (Info(A))
SINON
Eval ← Calcul(Eval(Fg(A)), Info(A), Eval(Fd(A)))
FSI

50. PARTIE III:
ARBRES BINAIRES DE
RECHERCHE(ABR)

51.  Définition
 Complexité
 Parcours
 Opérations de Recherche et de mise à jours (Insertion et
Suppression)
 Exemples d’application: Tri par ABR
51
PLAN DE LA PARTIE III

52. 52
DÉFINITION
 Un Arbre Binaire de Recherche (ABR) est un arbre
binaire ordonné tel que pour tout nœud n:
 Toutes les valeurs du sous-arbe gauche de n sont strictement
inférieures à la valeur de n, et
 Toutes les valeurs du sous-arbre droit de n sont supérieures ou
égales à la valeur de n.

53. 53
DÉFINITION
 Un Arbre Binaire de Recherche (ABR) est un arbre
binaire ordonné tel que pour tout nœud « i »:
 Toutes les valeurs du sous-arbre gauche de « i » sont strictement
inférieures à la clé de « i », et
 Toutes les valeurs du sous-arbre droit de « i » sont supérieures ou
égales à la clé de « i ».
 Intérêt de cette propriété : diminuer la complexité
temporel de recherche, d’insertion et de suppression dans
l’arbre

54. 54
COMPLEXITÉ
 Intérêt de cette propriété : diminuer la complexité
temporel de recherche, d’insertion et de suppression dans
l’arbre
O (n)
O (h) tel que h = log2(n) dans un
arbre équilibré
87 ?

55. 55
PARCOURS
 Voici un exemple d’un ABR contenant des valeurs
entières, appliquer les différents parcours vus sur les
arbres binaires. 20
15 59
5
3 10
27 71
33
8
55
52
 Le parcours inordre de cet arbre donne la liste ordonnée
suivante : 3, 5, 8, 10, 15, 20, 27, 33, 52, 55, 59, 71

56. 56
OPÉRATION DE RECHERCHE
 La recherche est dichotomique, à chaque étape, un sous
arbre est éliminé:
 Rechercher (55)
 Rechercher (FD(20))
 Rechercher (FG(59))
 Rechercher (FD(27))
 Rechercher (FD (33))
 Élément trouvé
20
15 59
5
3 10
27 71
33
8
55
52
55 ?

57. 57
OPÉRATION DE RECHERCHE
Fonction RechercherABR (R:*Tnoeud, x: entier) : * Tnoeud
Fin
Fonction RechercherABR (R:*Tnoeud, x: entier) : * Tnoeud
Debut
Si R = Null alors
Retourner (Null)
Sinon
Si Info (R) = x alors
Retourner (R)
Sinon
Si Info(R)>x alors
Retourner (RechercherABR (FG(R), x))
Sinon
Retourner (RechercherABR (FD(R), x))
Fin

58. 58
OPÉRATION D’INSERTION
 L'insertion d'un élément se fait toujours au niveau d'une
feuille. Cette insertion dans un ABR doit maintenir la
propriété des arbres de recherche, ainsi:
1. Rechercher la position d’insertion
2. Raccorder le nouveau nœud à son parent

59. 59
OPÉRATION D’INSERTION
 RechercherPosition (25)
 Rechercher (FD(20))
 Rechercher (FG(59))
 Position trouvé pour l’insertion, le père est le nœud 27
 Insérer 25 au niveau de la feuille dont le père est 27
20
15 59
5
3 10
27 71
33
8
55
52
+ 25
25

60. 60
OPÉRATION D’INSERTION
Fonction InsererABR (R:*Tnoeud, x: entier) : * Tnoeud
Debut
Si R = Null alors
RCreerNoeud(x)
Sinon
Si Info(R)>x alors
Aff_FG(R, InsererABR (FG(R), x))
Sinon
Aff_FD(R, InsererABR (FD(R), x))
Retourner (R)
Fin

61. 61
OPÉRATION DE SUPPRESSION
 Pour supprimer le nœud « i » d’un ARB, il faudra le
rechercher. Une fois le nœud « i » trouvé, on se trouve
dans une des situations suivantes :

62. 62
OPÉRATION DE SUPPRESSION
 Cas 1: Suppression d'une feuille
 Il suffit de l'enlever de l'arbre vu qu'elle n'a pas de fils.
 Exemple: supprimer le nœud i qui contient la valeur 8
1. Rechercher(8)
2. Libérer le nœud « i »
« i »
20
15 59
5
3 10
27 71
33
8
55
52
12

63. 63
OPÉRATION DE SUPPRESSION
 Cas 2: Suppression d'un nœud avec un fils
 Il faut l'enlever de l'arbre en le remplaçant par son fils.
 Exemple: supprimer le nœud i qui contient la valeur 10
1. Rechercher(10)
2. Chainer le père de i avec le FD(i)
3. Libérer le nœud « i »
« i »
20
15 59
5
3 10
27 71
33
12 55
52

64. 64
OPÉRATION DE SUPPRESSION
 Cas 2: Suppression d'un nœud avec un fils
 Il faut l'enlever de l'arbre en le remplaçant par son fils.
 Exemple: supprimer le nœud i qui contient la valeur 10
1. Rechercher(10)
2. Chainer le père de i avec le FG(i)
3. Libérer le nœud « i »
« i »
20
15 59
5
3 10
27 71
33
55
52
8

65. 65
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 1: On échange le nœud à supprimer avec son successeur
le plus proche (le nœud le plus à gauche du sous-arbre droit) ou
son plus proche prédécesseur (le nœud le plus à droite du
sous-arbre gauche). Cela permet de garder une structure d'arbre
binaire de recherche. 34
66
50
56
55
71
70
69
81
22
8
17
9
29
25
23 32
Le plus proche
prédécesseur
Le plus proche
successeur

66. 66
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 1  Cas A: On échange le nœud à supprimer avec son
successeur le plus proche (le nœud le plus à gauche ou le plus
petit du sous-arbre)
 Racine: 71
 La plus petite valeur : 69
34
66
50
56
55
71
70
69
81
22
8
17
9
29
25
23 32

67. 67
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 1  Cas A: On échange le nœud à supprimer avec son
successeur le plus proche (le nœud le plus à gauche ou le plus
petit du sous-arbre)
 Racine: 71
 La plus petite valeur : 69
34
66
50
56
55
71
70
69
81
Fonction Successeur (R: *Tnoeud): *Tnoeud
Fin
Fonction Successeur (R: *Tnoeud): *Tnoeud
Debut
RFD(R)
Si R≠Null alors
TQ FG(R)≠Null faire RFG(R)
Retourner (R)
Fin

68. 68
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 1  Cas A: On échange le nœud à supprimer avec son
plus proche prédécesseur (le nœud le plus à droite ou le plus
grand du sous-arbre gauche).
 Racine: 50
 La plus petite valeur : 56
34
66
50
56
55
71
70
69
81
22
8
17
9
29
25
23 32

69. 69
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 1  Cas A: On échange le nœud à supprimer avec son
plus proche prédécesseur (le nœud le plus à droite ou le plus
grand du sous-arbre gauche).
 Racine: 50
 La plus petite valeur : 56
34
66
50
56
55
71
70
69
Fonction Predecesseur (R: *Tnoeud): *Tnoeud
Fin
Fonction Predecesseur (R: *Tnoeud): *Tnoeud
Debut
RFG(R)
Si R≠Null alors
TQ FD(R)≠Null faire RFD(R)
Retourner (R)
Fin

70. 70
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Etape 2: on applique à nouveau la procédure de suppression qui
est maintenant une feuille ou un nœud avec un seul fils.
 Ainsi, si on choisit d’échanger le nœud « 66 » avec son plus proche
successeur « 69 », on obtient
34
66
50
56
55
71
70
69
81
22
8
17
9
29
25
23 32
69

71. 71
OPÉRATION DE SUPPRESSION
 Cas 3: Suppression d'un nœud avec deux fils
 Puis on applique à nouveau la procédure de suppression qui est
maintenant une feuille ou un nœud avec un seul fils.
 Ainsi, si on choisit d’ échanger le nœud « 66 » avec son plus proche
prédécesseur « 56 », on obtient
34
66
50
55
71
70
69
81
22
8
17
9
29
25
23 32
56

72. 72
OPÉRATION DE SUPPRESSION
 En conclusion, pour supprimer le nœud « i » d’un ARB, il
faudra le rechercher. Une fois le nœud « i » trouvé, on se
trouve dans une des situations suivantes :
Cas
« i »
Action
FG FD
Feuille Null Null Remplacer « i » par Null
Avec un
fils
Null ≠Null Remplacer « i » par FD(i)
≠Null Null Remplacer « i » par FG(i)
Avec
deux
fils
≠Null ≠Null
1. Rechercher le plus proche
prédécesseur ou successeur de « i »,
soit P.
2. Remplacer Info(i) par Info(P)
3. Remplacer P par FG(P) ou FD(P)

73. 73
OPÉRATION DE SUPPRESSION
Fonction SupprimerABR (R:*Tnoeud, x: entier) : * Tnoeud
Debut
Si R = Null alors
Retourner (R)
Sinon
Si Info(R)>x alors
Aff_FG(R, SupprimerABR (FG(R), x))
Retourner (R)
Sinon
Si Info(R)<x alors
Aff_FD(R, SupprimerABR (FD(R), x))
Retourner (R)
Sinon // Info(R) = x
Retourner (SupprimerRacine (R))
Fin

74. 74
OPÉRATION DE SUPPRESSION
Fonction SupprimerRacine (R:*Tnoeud) : * Tnoeud
Debut
Si FG(R) = Null alors
Si FD(R) = Null alors //Cas n°1: R est une feuille
LibérerNoeud(R)
Retourner (Null)
Sinon //Cas n°2: R possède un FD
DFD(R)
LibérerNoeud(R)
Retourner (D)
Sinon
Si FD(Q) = Null alors //Cas n°2: R possède un FG
GFG(R)
LibérerNoeud(R)
Retourner (G)
Sinon // Cas n°3: R possède deux fils
SSuccesseur (R)
Aff_Info (R, Info(S))
Aff_FD(R, SupprimerABR (DF(R), Info(S)))
Retourner (R)
Fin

75. 75
EXEMPLE D’APPLICATION: TRI PAR ABR
 Étant donné un tableau d’entiers T (n: sa taille), dire
comment peut on trier ce tableau en utilisant un Arbre
Binaire de Recherche (ABR)?
 Exemple:
20 15 10 35 19 13 5 3 12 7 16 40 25 38

76. 76
1. Insérer toutes les éléments du tableau dans un
ABR
20 15 10 35 19 13 5 3 12 7 16 40 25 38
20
15 35
10
19
5 13
3 7 12
25 40
38
16
EXEMPLE D’APPLICATION: TRI PAR ABR

77. 77
2. Parcourir l’ABR en inordre : GRD
3 5 7 10 12 13 15 16 19 20 25 35 38 40
20
15 35
10
19
5 13
3 7 12
25 40
38
16
EXEMPLE D’APPLICATION: TRI PAR ABR

78. 78
Procedure Tri_ARB(Var T: Tableau, n: entier)
Debut
RNull
Pour i0 à n-1 faire RInsererABR (R, T[i]).
Inordre (R, T); //Parcours Infixe
Fin
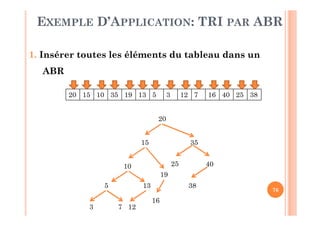
EXEMPLE D’APPLICATION: TRI PAR ABR
Indice est une variable globale initialisée à 0
Procedure Inordre (R: *Tnœud, Var T: Tableau)
Si ( R  Null) alors //Arbre n’est pas vide
Inordre(FG(R), T))
T[indice]Info(R) //Écrire la valeur dans le tableau
indice++
Inordre(FD(R), T)

79. PARTIE IV:
ARBRES BINAIRES DE
RECHERCHE ÉQUILIBRÉS
(ARBRES AVL)

80.  Introduction
 Définition
 Techniques d’équilibrage
 Opérations de Base: Recherche, Insertion et
Suppression
80
PLAN DE LA PARTIE IV

81. 81
INTRODUCTION
 La complexité au meilleur des cas de la recherche, de
l’insertion et de la suppression dans un ABR est O(h), où
h est la hauteur (ou profondeur) de l’arbre. Ce cas est
atteint par des arbres équilibrés
 Cependant, la complexité au pire cas pour un arbre à n
nœuds, est O(n). Ce cas est atteint par des arbres très
déséquilibrés, ou «filiformes».
 Plusieurs espèces des arbres équilibrés ont été
développés: les arbres AVL, les arbres 2-3, les arbres
rouge et noir, etc.

82. 82
INTRODUCTION
O (n)O (h) tel que h = log2(n)
87 ?
ABR Equilibré Filiformes

83. 83
DÉFINITION
 Les arbres AVL ont été introduits par les finlandais Adelson-
Velskii et Landis dans les années 60.
 Un arbre AVL est un ABR équilibré dont:
 la différence de hauteur (ou profondeur) entre le sous-
arbre gauche et le sous-arbre droit d'un nœud « R » diffère
d'au plus 1.
|Profondeur(FG(R) ) – Profondeur(FD(R)) | ≤ 1
 les arbres gauches et droits d'un nœud sont des arbres
AVL.
 Un champs supplémentaire est ajouté à tous les nœuds: c’est le
facteur de déséquilibre (appelé aussi facteur de balance «
Bal ») qui est calculé après chaque insertion/suppression.

84. 84
EXEMPLE
100
50
30 80
200
10
150
40
 Exemple: soit l’ABR suivant. Est-il un arbre AVL?
+1
+1 +1
0 0 0
0
Notons:
 qu’une feuille est un
arbre de hauteur 0,
 et que l’arbre vide a la
hauteur −1.
 L’arbre vide et l’arbre
réduit à une feuille,
sont des arbres AVL
Cet arbre est un arbre AVL
À vérifier pour chaque nœud R, on a:
| Profondeur(FG(R) ) – Profondeur(FD(R)) | <= 1

85. 85
EXEMPLE
 Exemple: Cet ABR est un arbre AVL avant insertion
Insérer la valeur 5 100
50
30 80
200
10
150
40
+1
+1 +1
0 0 0
0 0

86. 86
EXEMPLE
 Exemple: Cet ABR est un arbre AVL avant insertion
Insérer la valeur 5 100
50
30 80
200
10
150
40
Cet arbre n’est pas un arbre AVL après insertion de 5
 arbre déséquilibré
50
+1
+1
0
+1
0 0
+2Après insertion, calculer le
facteur de déséquilibre de
chaque nœud.

87. 87
EXEMPLE
 Exemple: Cet ABR est un arbre AVL avant insertion
Insérer la valeur 45 100
50
30 80
200
10
150
40
+1
+1 +1
0 0 0
0 0

88. 88
EXEMPLE
 Exemple: Cet ABR est un arbre AVL avant insertion
Insérer la valeur 45
Cet arbre n’est pas un arbre AVL après insertion de 45
 arbre déséquilibré
100
50
30 80
200
10
150
40
450
0
-1
-1
+1
0 0
+2

89. 89
TECHNIQUES D’ÉQUILIBRAGE
 L’opération d’équilibrage, appelée rotation, s’applique à tous les
arbres binaires.
 Le but des rotations est de pouvoir rééquilibrer un ABR.
 On opère donc une rotation gauche lorsque l’arbre est
«déséquilibré à droite», i.e. son sous-arbre droit est plus haut
que son sous-arbre gauche.
 On opère une rotation droite dans le cas contraire à savoir son
sous-arbre gauche est plus haut que son sous-arbre droit.
 Les rotations ne sont donc définies que pour les arbres binaires non
vides dont le sous-arbre gauche (pour rotation gauche) et sous-arbre
droit (pour rotation droite) n’est pas vide.
 Les rotations préservent l’ordre des données d’un ABR (parcours
inordre).

90. 90
TECHNIQUES D’ÉQUILIBRAGE
 Rotation simple : Rotation droite
 Soit A=(B, R, Z) un arbre binaire tel que B=(X, P, Y).
 La rotation droite est l’opération:
((X, P, Y), R, Z) → (X, P, (Y, R, Z))
R
P
X
(hauteur
h+1)
Déséquilibre gauche
Y
(hauteur
h)
Z
(hauteur
h)
P
R
X
(hauteur
h+1)
Y
(hauteur
h)
Z
(hauteur
h)
+1
+2
0
0
Rotation droite

91. 91
TECHNIQUES D’ÉQUILIBRAGE
 Rotation simple : Rotation droite
 Soit A=(B, R, Z) un arbre binaire tel que B=(X, P, Y).
 La rotation droite est l’opération:
((X, P, Y), R, Z) → (X, P, (Y, R, Z))
R
P
X
(hauteur
h)
Déséquilibre gauche
Y
(hauteur
h)
Z
(hauteur
h-1)
P
R
X
(hauteur
h)
Y
(hauteur
h)
Z
(hauteur
h-1)
0
+2
-1
+1
Rotation droite

92. 92
TECHNIQUES D’ÉQUILIBRAGE
 Rotation simple : Rotation gauche
 Soit A=(X, R, B) un arbre binaire tel que B=(Y, P, Z).
 La rotation gauche est l’opération:
( X, R, (Y, P, Z)) → ((X, R, Y), P, Z)
P
R
X
(hauteur h)
Y
(hauteur h)
Z
(hauteur
h+1)
R
P
Déséquilibre droit
X
(hauteur
h)
Y
(hauteur
h)
Z
(hauteur
h+1)
-1
-2
0
0Rotation gauche

93. 93
TECHNIQUES D’ÉQUILIBRAGE
 Rotation simple : Rotation gauche
 Soit A=(X, R, B) un arbre binaire tel que B=(Y, P, Z).
 La rotation gauche est l’opération:
( X, R, (Y, P, Z)) → ((X, R, Y), P, Z)
P
R
X
(hauteur h-1)
Y
(hauteur
h)
Z
(hauteur
h)
R
P
Déséquilibre droit
X
(hauteur
h-1)
Y
(hauteur
h)
Z
(hauteur
h)
0
-2
-1
+1Rotation gauche

94. 94
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation gauche-droite
 C’est une rotation gauche sur le sous arbre-gauche du nœud r
suivie d’une rotation droite sur le nœud r
P
Q
R
D
(h)
C
(h)
B
(h)
A
(h)
Q
P
R
D
(h)
C
(h)
B
(h)
A
(h)
Rotation gauche Rotation droite
Q
P R
D
(h)
C
(h)
B
(h)
A
(h)
((((A,A, P,P, ((B,B, Q,Q, CC)))),, R,R, D)D) →→ ((((((A,A, P,P, BB)),, Q,Q, CC)),, R,R, D)D) →→ ((((A,A, P,P, BB)),, Q,Q, ((C,C, R,R, DD))))
0
0
-1
+2
0
+1
0
0+2

95. 95
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation gauche-droite
 C’est une rotation gauche sur le sous arbre-gauche du nœud r
suivie d’une rotation droite sur le nœud r
P
Q
R
D
(h)
C
(h-1)
B
(h)
A
(h)
Q
P
R
D
(h)
C
(h-1)
B
(h)
A
(h)
Rotation gauche Rotation droite
Q
P R
D
(h)
C
(h-1)
B
(h)
A
(h)
((((A,A, P,P, ((B,B, Q,Q, CC)))),, R,R, D)D) →→ ((((((A,A, P,P, BB)),, Q,Q, CC)),, R,R, D)D) →→ ((((A,A, P,P, BB)),, Q,Q, ((C,C, R,R, DD))))
0
+1
-1
+2
0
+2
-1
0+2

96. 96
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation gauche-droite
 C’est une rotation gauche sur le sous arbre-gauche du nœud r
suivie d’une rotation droite sur le nœud r
P
Q
R
D
(h)
C
(h)
B
(h-1)
A
(h)
Q
P
R
D
(h)
C
(h)
B
(h-1)
A
(h)
Rotation gauche Rotation droite
Q
P R
D
(h)
C
(h)
B
(h-1)
A
(h)
((((A,A, P,P, ((B,B, Q,Q, CC)))),, R,R, D)D) →→ ((((((A,A, P,P, BB)),, Q,Q, CC)),, R,R, D)D) →→ ((((A,A, P,P, BB)),, Q,Q, ((C,C, R,R, DD))))
+1
-1
-1
+2
+1
+1
0
0+2

97. 97
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation droite-gauche
 C’est une rotation droite sur le sous arbre-droit du nœud r suivie
d’une rotation gauche sur le nœud r
Rotation droite Rotation gauche
(A,(A, R,R, ((((B,B, Q,Q, CC)),, P,P, DD)))) →→ (A,(A, R,R, ((B,B, Q,Q, ((C,C, P,P, DD)))))) →→ ((((A,A, R,R, BB)),, Q,Q, ((C,C, P,P, DD))))
P
Q
R
A
(h)
0
+1
-2
B
(h)
C
(h)
D
(h)
Q
P
R
0
-1
-2
A
(h)
B
(h)
C
(h)
D
(h)
Q
R P
0 0
0
A
(h)
B
(h)
C
(h)
D
(h)

98. 98
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation droite-gauche
 C’est une rotation droite sur le sous arbre-droit du nœud r suivie
d’une rotation gauche sur le nœud r
Rotation droite Rotation gauche
(A,(A, R,R, ((((B,B, Q,Q, CC)),, P,P, DD)))) →→ (A,(A, R,R, ((B,B, Q,Q, ((C,C, P,P, DD)))))) →→ ((((A,A, R,R, BB)),, Q,Q, ((C,C, P,P, DD))))
P
Q
R
A
(h)
+1
+1
-2
B
(h)
C
(h-1)
D
(h)
Q
P
R
-1
-1
-2
A
(h)
B
(h)
C
(h-1)
D
(h)
Q
R P
0 -1
0
A
(h)
B
(h)
C
(h-1)
D
(h)

99. 99
TECHNIQUES D’ÉQUILIBRAGE
 Rotation double : double rotation droite-gauche
 C’est une rotation droite sur le sous arbre-droit du nœud r suivie
d’une rotation gauche sur le nœud r
Rotation droite Rotation gauche
(A,(A, R,R, ((((B,B, Q,Q, CC)),, P,P, DD)))) →→ (A,(A, R,R, ((B,B, Q,Q, ((C,C, P,P, DD)))))) →→ ((((A,A, R,R, BB)),, Q,Q, ((C,C, P,P, DD))))
P
Q
R
A
(h)
-1
+1
-2
B
(h-1)
C
(h)
D
(h)
Q
P
R
0
-2
-2
A
(h)
B
(h-1)
C
(h)
D
(h)
Q
R P
1 0
0
A
(h)
B
(h-1)
C
(h)
D
(h)

100. 100
OPERATIONS DE BASE
 La recherche est identique à celui des ABR car les
arbres AVL sont avant tout des ABR équilibrés.
 L’insertion d’un élément dans un arbre AVL peut
provoquer un déséquilibre. Donc, pour rétablir l’équilibre
(rééquilibrer) de l’arbre après une insertion, une seule
rotation ou double rotation suffit.
 La suppression d’un élément dans un arbre AVL peut
provoquer un déséquilibre. Donc pour rétablir l’équilibre
(rééquilibrer) de l’arbre après une suppression, il faut
jusqu’à h rotations (h est la hauteur de l’arbre) ou double
rotations.

101. 101
INSERTION
 L’ajout d’un nœud se fait toujours au niveau d’une feuille,
puis on rééquilibre l’arbre AVL si l’insertion a
déséquilibré l’arbre.
 Le déséquilibre est rencontré lorsque le facteur
d’équilibrage d’un nœud de l’arbre égale à ± 2.

102. 102
INSERTION
 Exemple: soit la série de nombres à insérer dans un
arbre AVL (2 10 12 4 16 8 6 14 )
2 10 12 4 16 8 6 14
2
0
2 10 12 4 16 8 6 14
2
10 0
-1
2 10 12 4 16 8 6 14
2
10
12 0
-1
-2
Rotation simple
10
122 00
0

103. 103
INSERTION
 Exemple: soit la série de nombres à insérer dans un
arbre AVL (2 10 12 4 16 8 6 14 )
2 10 12 4 16 8 6 14
10
122
4 0
-1 0
1
2 10 12 4 16 8 6 14
10
122
4 16 00
-1-1
0

104. 104
INSERTION
 Exemple: soit la série de nombres à insérer dans un
arbre AVL (2 10 12 4 16 8 6 14 )
2 10 12 4 16 8 6 14
10
122
4 16
8 0
-1
-2
0
-1
1
Rotation
simple
10
124
8 1620 0
0
-10
0

105. 105
INSERTION
 Exemple: soit la série de nombres à insérer dans un
arbre AVL (2 10 12 4 16 8 6 14 )
2 10 12 4 16 8 6 14
10
124
8 162
6 0
10
-1
0
-1
1

106. 106
INSERTION
 Exemple: soit la série de nombres à insérer dans un
arbre AVL (2 10 12 4 16 8 6 14 )
2 10 12 4 16 8 6 14
10
124
8 162
6 14
0
0
1
-2
10
-1
0
Rotation
double
10
144
8 162
6
12
0
1
0 0
0-1
1
0

107. 107
INSERTION
 Exemple 2: soit l’arbre suivant, donner le résultat après
insertion de 7
10
144
8 162
6
12
1 9

108. 108
INSERTION
 Exemple 2: soit l’arbre ci-dessus, donner le résultat
après insertion de 7
0
10
144
8 162
6
12
-1
1
0 0
0
1
-1
2
10
9 0
7
Nœud inséré
10
14
4
8
16
2 6
12
-1
0
0
1
-1
10
9
07 0
0
0
0
Rotation
double

109. 109
INSERTION
R
h h
R
hh+1
R
h h+1
R
hh+2
R
hh+1
R
h+1h+1
R
h h+2
R
h+1 h+1
R
h h+1
0
+1
-1
+1
+2
0
-1
0
-2
AvantAprès insertion à gauche Après insertion à droite
Cas A
Cas B

110. 110
INSERTION
 Remarques:
 Après une insertion, seules les nœuds qui sont sur le chemin du
point d’insertion à la racine sont susceptibles d’être déséquilibrés.
 Cas A: L’arbre devient non équilibré quand le nouveau nœud
inséré est un descendant gauche d’un nœud qui avait un facteur
d’équilibrage égal à 1
 Cas B: L’arbre devient non équilibré quand le nouveau nœud
inséré est un descendant droit d’un nœud qui avait un facteur
d’équilibrage égal à -1

111. 111
INSERTION
R
hh+2
+2
R
h
+1
P
hh
0
Cas A
Si insertion dans le sous-arbre
gauche du fils gauche alors
Rotation Simple à droite
Si insertion dans le sous-arbre droit
du fils gauche alors Rotation
Double Gauche-Droite
R
h
+2
P
h
+1
h+1
R
h
+2
P
h
-1
h+1
Avant

112. 112
INSERTIONR
h h+2
-2 Cas B
R
h
-1
P
hh
0
R
h
P
h
-2
+1
h+1
R
h
P
hh
-2
-1
Si insertion dans le sous-arbre
droit du fils droit alors Rotation
Simple à gauche
Si insertion dans le sous-arbre gauche
du fils droit alors Rotation Double
Droite-Gauche
Avant

113. 113
SUPPRESSION
 Le principe de la suppression d’un élément dans un arbre
AVL est le même que dans un ABR, c.à.d. recherche de
l’élément à supprimer, suppression et remplacement, le
cas échéant, par l’élément qui lui immédiatement
inférieur ou supérieur.
 Après la première phase de la suppression, la hauteur de
l’arbre est diminué de 1. Le problème est que cet arbre
n’est plus forcément un arbre AVL. Il faut donc le
rééquilibrer.

114. 114
SUPPRESSION
 S’il y a déséquilibre, la rotation appliquée peut diminuer
à son tour la hauteur de l’arbre et générer un nouveau
déséquilibre. En fait les rotations peuvent s’enchainer en
cascade depuis l’élément supprimé jusqu’à la racine.
Ainsi, on peut faire jusqu’à h simple rotations ou double
rotations (h est la hauteur de l’arbre initial).

115. 115
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 10:
10
14
4
8
16
2 6
12
-1
0
0
1
-1
10
9
0
7
0
0
0
0
12
14
4
8
16
2 6 -1
-1
1
-1
10
9
0
7
0
0
0
0

116. 116
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 8:
12
14
4
8
16
2 6 -1
-1
1
-1
10
9
0
7 0
0
0
0
12
14
4
9
16
2 6 -1
-1
1
-2
10 0
7 0
0
0

117. 117
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 8:
12
14
4
9
16
2 6 -1
-1
1
-2
10 0
7 0
0
0
14
12
4
9
162 6 -1
0
1
0
10 0
7
0
0
1
RSG

118. 118
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 12 puis 16:
14
12
4
9
162 6 -1
0
1
0
10 0
7
0
0
1
144
9
2 6 -1
1
0
10 0
7
0
+2

119. 119
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 12 puis 16:
144
9
2 6 -1
1
0
10 0
7
0
+2
9
4
14
2
6 -1
1 1
1 0
0
7
0
-1
RSD

120. 120
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 30:
100
200
30
50
300
10 40
-1
-1
+1
20
80
60
0
+1
+1
-1
9070+1
0
00
0
40
50
300
10
-1
-1
+1
20
80
60
+2
+1
-1
9070
+1
100
200
0
0
0
0

121. 121
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 30:
40
50
300
10
-1
-1
+1
20
80
60
+2
+1
-1
9070
+1
100
200
0
0
0
0
RDG-D
20
50
300
10
-1
+1
40 80
60
0
0
+1
-2
9070+1
100
200
0 0
0
0

122. 122
SUPPRESSION
 Exemple: soit l’arbre suivant. Donner le résultat après la
suppression de 30:
RDD-G
20
50
300
10
-1
+1
40 80
60
0
0
+1
-2
9070+1
100
200
0 0
0
0
20
80
30010
-1
-1
40
50
60
0
0
9070
+1
100
200
0
0 0 0
0
0

123. PARTIE V:
ARBRES M-AIRE DE
RECHERCHE (AMR)

124.  Définitions
 Modèle
 Opérations de Base: Recherche, Insertion et
Suppression
124
PLAN DE LA PARTIE V

125. 125
DÉFINITION
 Un arbre de recherche m-aire peut être défini comme une
généralisation de l'arbre de recherche binaire. Au lieu d'avoir
une clé et deux pointeurs, on aura « d-1 » clés et « d »
pointeurs.
 Un arbre de recherche m-aire d'ordre « d » est un arbre
dans lequel chaque nœud peut avoir « d » fils.

126. 126
DÉFINITION
 Si s1, s2, ... sd sont les « d » sous arbres issus d'un nœud
donné avec les clés k1, k2, ....,kd-1 dans l'ordre ascendant,
alors :
 Toutes les clés dans s1 sont inférieurs à k1
 Toutes les clés dans sj (j=2,3, ...d-1) sont supérieurs à kj-1 et
inférieur à kj
 Toutes les clés dans sd sont supérieurs kd-1.
s1 k1 s2 ….. kj-1 sj kj …... kd-1 sd
ki des données tq: k1 < k2 ....< kd-1

127. 127
DÉFINITION
 Propriété d’ordre:
s1 k1 s2 ….. kj-1 sj kj …... kd-1 sd
s11 k11 s12 k12 ....... s1(d-1) k1(d-1) s1d
sj1 kj1 sj2 kj2 ....... sj(d-1) kj(d-1) sjd
sd1 kd1 sd2 kd2 ....... sd(d-1) kd(d-1) sdd
ki des données tq: k1 < k2 ....< kd-1
(Éléments du s1) < k1 (Éléments du sd) > kd-1
kj-1 < (Éléments du sj) < kj
(j=2,3, ...d-1)

128. 128
EXEMPLE
 Soit l’arbre m-aires de recherche AMR d’ordre 4

129. 129
MODÈLE
 La structure de l’arbre ARM est la suivante:
Type TnœudAMR = Structure
Info : Tableau[0..d-2] d’entier
Fils : Tableau[0..d-1] de *TnoeudAMR
Degré : [0 .. d] (intervalle d’entier)
Fin

130. 130
MODÈLE
 Pour écrire des algorithmes sur ce type d'arbres, le modèle
doit être formé des opérations suivantes :
 CreerNoeud(x)
 Info(P, i)
 Fils (P, i)
 Degré(P)
 LibererNoeud(P)
 Aff_info(P, x, i)
 Aff_fils(P, Q, i)
 Aff_Degré(P, n)

131. 131
RECHERCHE
 La recherche dans un AMR ressemble beaucoup à celle
effectuée dans un ABR, excepté qu’au lieu de prendre à
chaque nœud une décision de branchement binaire (Fils
gauche ou droit), on prend une décision à options multiples,
selon le nombre de fils du nœud.

132. 132
RECHERCHE
 Exemple: Rechercher l’élément 68.
On récupère l’adresse du nœud (nœud P) ainsi la position
dans le nœud (soit pos = 2) où l’élément 68 doit exister.

133. 133
INSERTION
 L’insertion se déroule comme suit:
1. Rechercher l’élément à insérer « x »:
RechercherAMR(R, x, Var P, Var pos, Var trouve).
2. Si l’élément n’est pas trouvé (trouve = faux)
a. Si le tableau « Info » du nœud « P » n’est pas plein alors
insérer l’élément à sa position « pos » dans ce tableau «
Info ».
b. Sinon le tableau « Info » du « P » est plein alors créer un
nouveau nœud contenant l’élément « x » à insérer
ensuite placer comme fils numéro « pos » du « P »

134. 134
INSERTION
 Exemple: Insérer les éléments suivants: 1, 40, 68, 170.
1 6 10 37 40
68
170

135. 135
SUPPRESSION
 On distingue deux types de suppression:
1. Suppression logique:
 Laisser la clé au niveau du nœud et le marquer comme
supprimé
 Le nœud reste utilisé pour l'algorithme de recherche
 L’insertion d’un nœud supprimé consiste à le marquer
comme non supprimé
2. Suppression physique: Technique similaire à celle
des ABR

136. 136
SUPPRESSION
 Suppression physique:
a. Si l’élément à supprimer est le seul élément dans le
nœud alors libérer le nœud.
 Exemple: supprimer 37 ou 110

137. 137
SUPPRESSION
 Suppression physique:
b. Si l’élément à supprimer a un sous arbre gauche ou
droit vide alors supprimer l’élément, ensuite tasser le
nœud (décalage dans le nœud + changer l’adresse du
fils).
 Exemple: la suppression du 65 entraîne le décalage de 69 à la
position de 65 ainsi le déplacement du fils droit de 65.
68
62 69
68

138. 138
SUPPRESSION
 Suppression physique:
b. Si l’élément à supprimer a un sous arbre gauche ou
droit vide alors supprimer l’élément, ensuite tasser le
nœud (décalage dans le nœud + changer l’adresse du
fils).
 Exemple: la suppression du 120 entraîne le décalage de 150 à
la position de 120.
68
100 120
110

139. 139
SUPPRESSION
Suppression physique:
c. Si l’élément à supprimer a des sous arbres gauche et
droit tous les deux non vides alors remplacer l’élément
à supprimer par son successeur/prédécesseur, ensuite
supprimer ce successeur/prédécesseur
 Exemple: la suppression du 85 entraîne le remplacement du
85 par 100 , ensuite la suppression du 100
120 150
110
12 50 100

140. PARTIE VI:
B-ARBRES: AMR EQUILIBRÉS

141.  Introduction
 Définition
 Opérations de Base: Insertion et Suppression
141
PLAN DE LA PARTIE VI

142. 142
INTRODUCTION
 Le problème avec les AMR est celui du maintien de
l'équilibre de l'arbre i.e. tous ses feuilles sont au même
niveau.
 Bayer et McCreight (en 1970) ont fourni une solution à ces
problèmes par l'invention des B-arbres (B pour Bayer /
Boeng / Balanced).

143. 143
DÉFINITION
Un B-arbre d'ordre d (tel que d= 2*m +1) est défini comme
suit :
La racine, si elle n’est pas une feuille, a au moins 2 fils.
Chaque nœud contient k clés avec:
 1≤k≤2*m (nœud racine)
 m≤k≤2*m (nœud non racine)
Tous les nœuds feuilles sont au même niveau.

144. 144
INSERTION
 L’insertion se fait toujours au niveau des feuilles.
 Ainsi, l’insertion se déroule comme suit:
1. Rechercher la position de l’élément à insérer, soit P le
nœud trouvé.
2. Si le nœud (P) n’est pas plein alors insérer la clé à sa
bonne position dans le nœud.

145. 145
INSERTION
 Exemple: Considérons le B-arbre suivant d'ordre 3,
insérer les valeurs suivantes dans l’ordre : 55, 57, 95, 85, 87.

146. 146
INSERTION
2. Si le nœud (P) n’est pas plein alors insérer la clé à sa
bonne position dans le nœud.
3. Sinon, si le nœud (P) est plein, l’éclatement se fait en
cascade (approche ascendante) comme suit
a. Classer les clés dans l’ordre croissant : a1, a2, …ad; soit
amil la clé du milieu
b. déplacer les clés amil+1 … ad dans un nouveau nœud (Q)
c. Insérer la valeur du milieu amil dans le nœud père (aller
à 2) de telle sorte que le nœud P se trouvera à sa
gauche et Q à sa droite.

147. 147
INSERTION
 Exemple: Considérons le B-arbre suivant d'ordre 3,
insérer les valeurs suivantes dans l’ordre : 55, 57, 95, 85, 87.

148. 148
INSERTION
 Exemple: Considérons le B-arbre suivant d'ordre 3,
insérer les valeurs suivantes dans l’ordre : 55, 57, 95, 85, 87.

149. 149
SUPPRESSION
 Il faut supprimer l‘élément tout en préservant la qualité
de B-arbre, c'est à dire en gardant au moins m clés dans le
nœud (non racine).
 C'est le cas de la suppression physique dans un Arbre de
M-aire Recherche (AMR). En plus, si le nœud feuille qui
contenait la clé à supprimer a moins de m clés, alors l'action
suivante est entreprise :

150. 150
SUPPRESSION
 Cas 1: Si l'un des frères (gauche ou droit) contient plus de
m clés, alors la clé, soit Ks, dans le nœud père qui sépare
entre les deux frères est ajoutée au nœud "underflow" et le
dernier (si frère droit) ou le premier élément (si frère gauche)
est ajoutée au père à la place de Ks.
Suppression de 113
B-arbre d’ordre 5

151. 151
SUPPRESSION
 Cas 2-a: Si les deux frères contenaient exactement m clés,
le nœud "underflow" et l'un de ses frères seront concaténés (
fusionnés ou consolidés) en un seul nœud qui contient aussi
la clé séparatrice de leur père.
Suppression de 120
B-arbre d’ordre 5

152. 152
SUPPRESSION
 Cas 2-b: Il est aussi possible que le père contient
seulement m clés et par conséquent il n'a pas de clé à
donner. Dans ce cas, il peut emprunter de son père et frère.
Suppression de 65
B-arbre d’ordre 5

153. 153
SUPPRESSION
 Cas 2-c: Dans le pire des cas, quand les frères du père
n'ont pas des clés à donner, le père et son frère peuvent aussi
être concaténés et une clé est prise du grand père.
Suppression de 173
B-arbre d’ordre 5

154. 154
SUPPRESSION
 Cas 2-d: Si tous les antécédents d'un nœud et leurs frères
contiennent exactement m clés, une clé sera prise de la
racine (due aux concaténations en cascades):
Si la racine avait plus d'une clé, ceci termine le
processus.
Si la racine contenait une seule clé, elle sera utilisée
dans la concaténation. Le nœud racine est libéré et la
profondeur de l'arbre est réduit d'une unité.

155. SOURCES DE CE COURS
 N. EL-ALLIA , Cours d’Algorithmique et Structures de données dynamiques, Ecole
nationale Supérieure d’Informatique (ESI), 2014.
 Djamel Eddine ZEGOUR, Cours de Structures de Données, Ecole nationale
Supérieure d’Informatique (ESI), Disponible sur
http://zegour.esi.dz/Cours/Cours_sdd.htm
 W. K. Hidouci, Cours Structures De Données et Fichiers, École nationale Supérieure
d’Informatique, Disponible sur hidouci.esi.dz/algo/
 B. Boutoumi, Cours d’Algorithmique et Structures de données, Université Saad
Dahlab de Blida, 2014, Disponible sur https://sites.google.com/a/esi.dz/s-
aroussi/algorithmique-et-structure-de-donnees/nouveau-programme .
 A. Aroussi, Cours d’ Algorithmique et Structure de Données (ancien
programme/semestre 2), Université de Blida 1, 2015, Disponible sur
https://sites.google.com/a/esi.dz/s-aroussi/algorithmique-et-structure-de-
donnees/annee-universitaire-2014-2015/ancien-programme/semestre-2
155