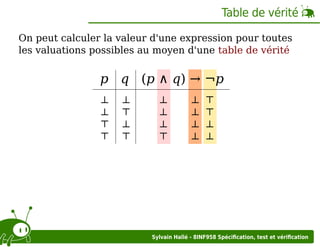
Le document examine l'utilisation de la logique mathématique et de la modélisation formelle pour résoudre des problèmes liés aux tests et à l'assurance qualité dans le développement logiciel. Il aborde des concepts tels que les propositions logiques, les valuations, les tables de vérité, et les quantificateurs, tout en offrant des exemples concrets pour illustrer ces notions. La démarche souligne l'importance de la précision dans la définition des problèmes et des relations entre variables pour parvenir à des conclusions logiques.































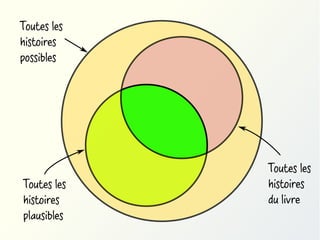
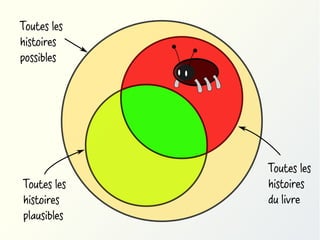
















































![Quantificateurs
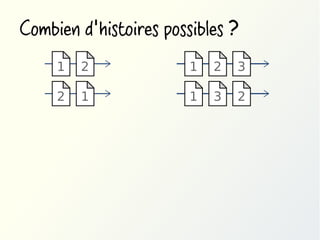
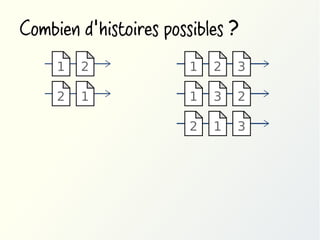
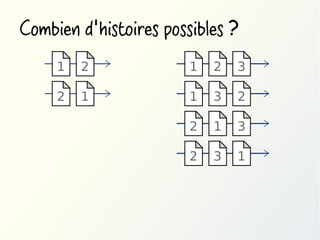
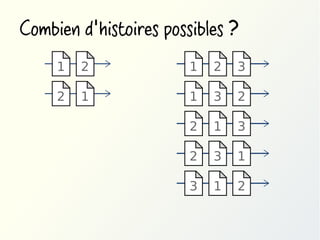
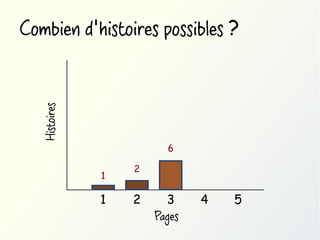
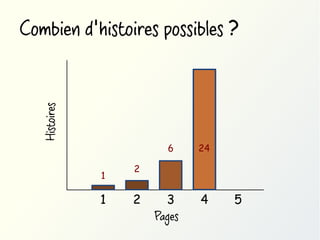
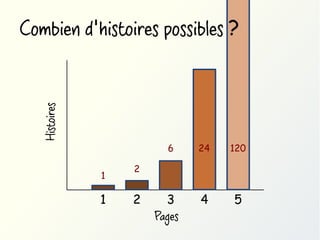
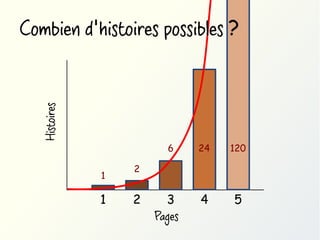
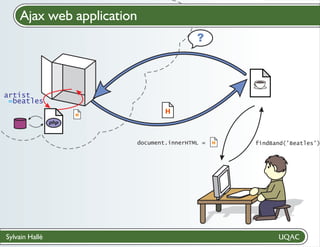
Méthode #2: utiliser des quantificateurs
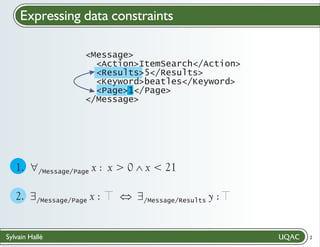
∀x : ∀y : (assassin(x) ∧ victime(y)) → déteste(x,y)
"pour tout x (pris dans l'ensemble E)"
Intuitivement, si E = {a, b, c, ..., k}, alors
∀x : φ ≡ φ[x/a] ∧ φ[x/b] ∧ ... ∧ φ[x/k]
où φ[x/a] est l'expression φ dans laquelle on a remplacé
tous les x par a
Ex.: ∀x : assassin(x) ≡ assassin(Agatha) ∧
assassin(Charles) ∧ assassin(Maître d'hôtel)
Sylvain Hallé - 8INF958 Spécification, test et vérification](https://image.slidesharecdn.com/inf9073-140123141811-phpapp01/85/A-la-chasse-aux-bugs-avec-la-Laboratoire-d-informatique-formelle-122-320.jpg)






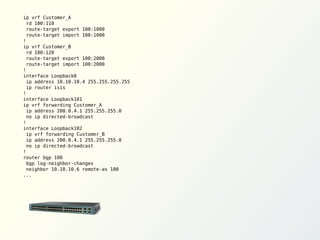





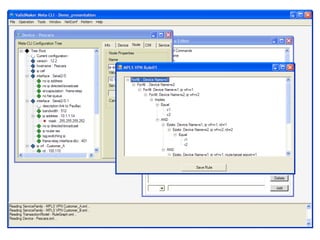



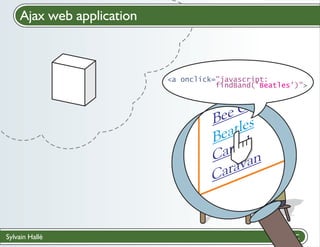
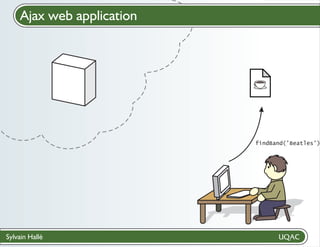
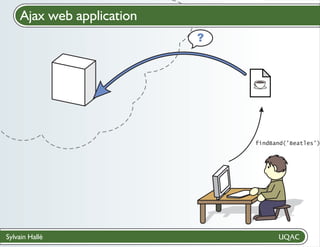
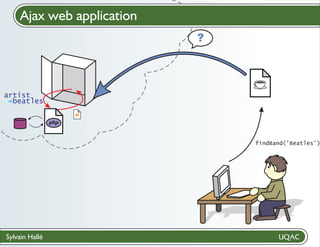
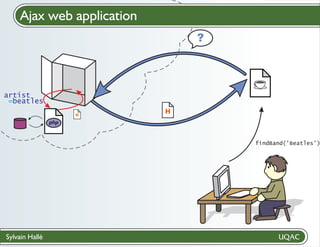




















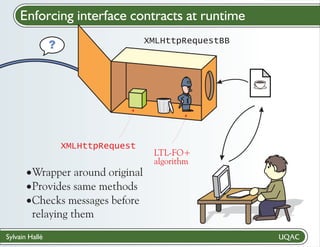




![Add BeepBeep to an application
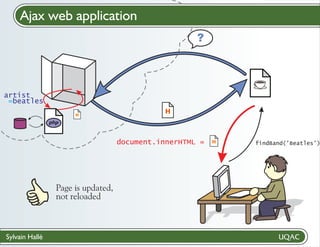
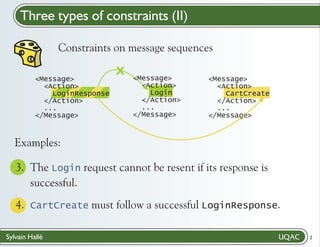
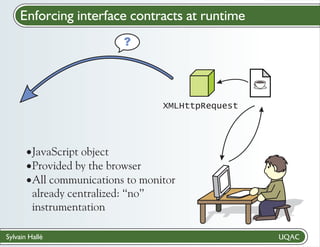
Create a contract
? file with LTL-FO+ formulas
# ------------------------------------------------------# BeepBeep contract file for the Beep Store
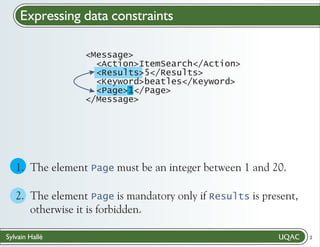
# ------------------------------------------------------% The element Page must be an integer between 1 and 20.
; G ([p /Message/Page] (((p) > ({0})) & ((p) < ({21}))))
% The element Page is mandatory only if Results is
present, otherwise it is forbidden.
; G ([a /Message/Action] (((a) = ({ItemSearch})) -> (
((<r /Message/Results> ({TRUE})) ->
(<p /Message/Page> ({TRUE}))) &
((<p /Message/Page> ({TRUE})) -> (
<r /Message/Results> ({TRUE}))))))
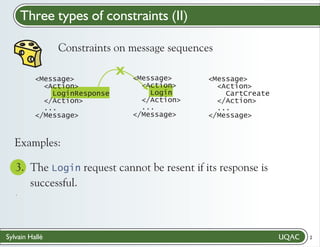
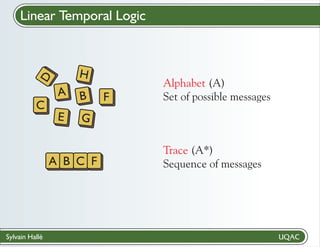
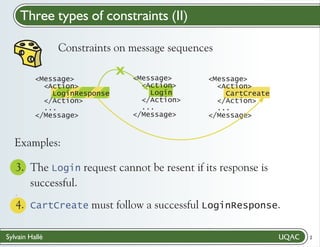
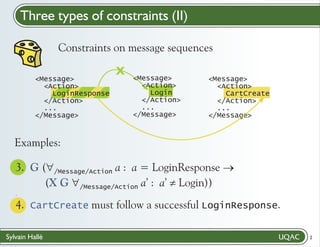
% The Login request cannot be resent if its response
is successful.
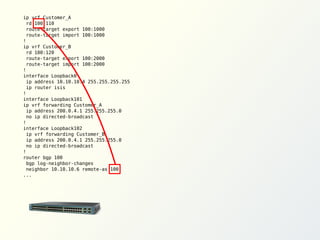
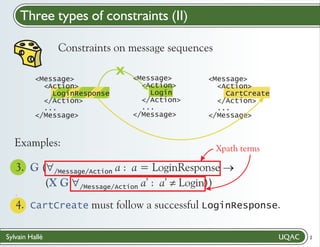
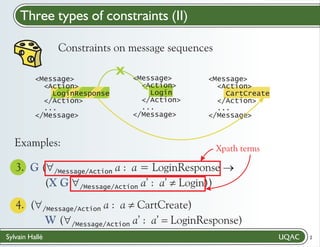
; G ([a /Message/Action] (((a) = ({LoginResponse})) ->
(X (G ([b /Message/Action] (!((b) = ({Login}))))))))
Sylvain Hallé
}
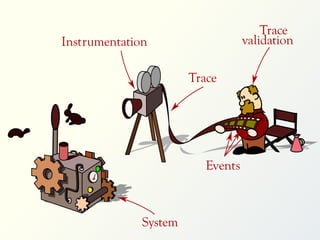
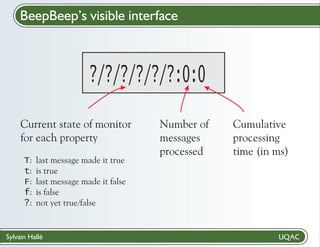
Caption: used
when violations
are discovered
Plain-text
LTL-FO+
(automatically
parsed)](https://image.slidesharecdn.com/inf9073-140123141811-phpapp01/85/A-la-chasse-aux-bugs-avec-la-Laboratoire-d-informatique-formelle-248-320.jpg)




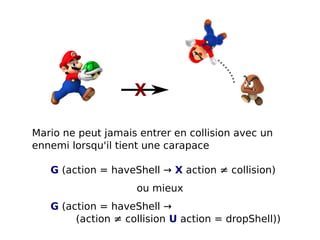

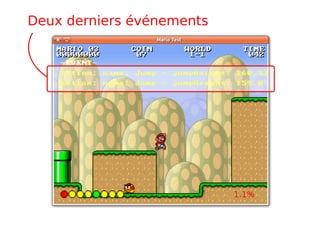

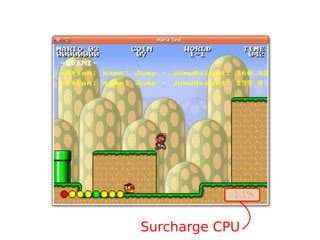

![COVERSTORY
Verified software
My computer won’t fail me
Web-browser crashes are annoying, but as far as software malfunctions go, the
consequences are mild. With a plane’s autopilot or the control room of a nuclear power
station, it’s another matter. As our lives become ever more saturated with computers,
how can we know they won’t fail? Currently, we systematically test all conceivable
scenarios under which they might. A better insurance might be logic. [...]
32 | New Scientist | 16 October 2010](https://image.slidesharecdn.com/inf9073-140123141811-phpapp01/85/A-la-chasse-aux-bugs-avec-la-Laboratoire-d-informatique-formelle-262-320.jpg)