Le document présente des algorithmes arithmétiques et leurs applications en langage Pascal, incluant des calculs de permutations, combinaisons, ainsi que des conversions entre bases de numération (décimale, binaire, hexadécimale). Plusieurs exemples et exercices sont fournis pour illustrer la fonctionnalité des programmes. L'auteur, Mohamed Sayari, insiste sur l'importance des procédures modulaires dans la programmation.

![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
b) Analyse de la procédure saisir Algorithme de la procédure saisir
DEF PROC saisir var (n, p : entier)
0) DEF PROC saisir (var n, p : entier)
Résultat = n, p
1) Répéter
2) N= [ ] répéter
Ecrire ("P= "), lire (P)
N= donnée ("N=")
Jusqu’à (p≥1)
Jusqu’à (n≥p)
2) Répéter
1) P= [ ] répéter Ecrire ("N= "), lire (N)
P= donnée ("P= ") Jusqu’à (N≥p)
Jusqu’à (p ≥1) 3) Fin saisir
c) Analyse de la fonction calcul Algorithme de la fonction calcul
DEF FN calcul (n, p : entier) : entier
0) DEF FN CALCUL (n, p : entier) : entier
2) Résultat = calcul a
1) A 1
1) A= [a1] pour i de n à (n-p+1) (pas=-1) Faire Pour i de n à n-p+1 (pas=-1) Faire
Aa*i Aa*i
Fin pour Fin pour
2) Calcul a
TDOL 3) Fin calcul
objet Tupe/nature
I Entier
a entier
2](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-2-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
III.3 Calcul de
Activité1 : écrire un programme modulaire en Pascal qui permet de calculer et d’afficher le avec n et p
deux entiers tel que 0≤p≤ n
a) Analyse du programme principal
2) Résultat = Ecrire ("C (", p, ",", n, ")=", FN calcul (n, p))
3) (N,p)= proc saisir (n, p)
Algorithme du programme principal
TDOG
0) DEBUT arrangement
Objet Type/Nature 1) Proc saisir (n, p)
N Entier 2) Ecrire ("C (", p, ",", n, ")=", FN calcul (n, p))
p entier 3) Fin arrangement
saisir procédure
calcul fonction
b) Analyse de la procédure saisir
DEF PROC saisir var (n, p : entier)
Résultat = n, p
2) N= [ ] répéter
Algorithme de la procédure saisir
N= donnée ("N=")
Jusqu’à (n≥p) 0) DEF PROC saisir (var n, p : entier)
1) P= [ ] répéter 1) Répéter
P= donnée ("P= ") Ecrire ("P= "), lire (P)
Jusqu’à (p ≥0) Jusqu’à (p≥0)
2) Répéter
Ecrire ("N= "), lire (N)
Jusqu’à (N≥p)
3) Fin saisir
c) Analyse de la fonction calcul
DEF FN calcul (n, p : entier) : real Algorithme de la fonction calcul
2) Résultat = calcul c
0) DEF FN CALCUL (n, p : entier) : réel
1) C FACT (n) / (FACT (p) * FACT (n-p))
1) C FACT (n) / (FAT(p)*FACT (n-p))
2) CALCUL c
3) Fin calcul
3](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-3-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
III.4 Application
=9 =8 =1
=1 =1
Activité : écrire la fonction combinaison récursive
Analyse de la fonction COMB récursive
DEF FN Combo (n, p : entier) : entier
Résultat= combo
1) combo= [ ] si (p=0) ou (p=n) alors combo 1
Sinon combo FN combo (n-1, p-1) + FN combo (n-1, p)
Fin si
4](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-4-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
IV. Quelques règles de divisibilité (livre page 166)
V. Conversion entre les bases de numération
V.1 Définition
Un système de numération est une méthode de comptage fondée sur une base de numération qui est
un entier supérieur ou égal à 2. Soit N une base de numération, le système sera doté de N chiffres de
0 à N-1
V.2 Exemples de bases de numération (voir livre page 166)
V.3 Conversion d’un nombre décimal en binaire
Ecrire un programme modulaire en pascal qui permet de saisir un entier positif, le convertit en
binaire.
a) Analyse du programme principal
2) Résultat = Ecrire (Fn conv_DEC_BIN(n))
1) N = proc saisir (n)
b) Analyse de la procédure CONV_DEC_BIN
DEF FN CONV_DEC_BIN (n : entier) : chaîne Algorithme du programme principal
2) Résultat = CONV_DEC_BIN ch
1)Ch=[ch ""] répéter 0) Début conversion
R n mod 2 1) Proc saisir (n)
N n div 2 2) Ecrire (Fn conv_DEC_BIN(n))
Ch chr(48+R)+ch 3) Fin conversion
Jusqu’à (n=0)
Algorithme de la fonction CONV_DEC_BIN
0) DEF FN CONV_DEC_BIN (n : entier) : chaîne
1) Ch ""
répéter
R n mod 2
N n div 2
Ch chr(48+R)+ch
Jusqu’à (n=0)
2) CONV_DEC_Bin ch
3) Fin CONV_DEC_BIN
5](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-5-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
V. 4 Conversion d’un nombre binaire en décimal
Ecrire un programme modulaire en pascal qui permet de saisir un nombre binaire (sous forme d’une
chaîne de caractères), le convertit en décimal.
Algorithme du programme principal
a) Analyse du programme principal
2) Résultat = Ecrire (FN conv_bin_dec(ch)) 0) Début conversion
1)Ch= proc saisir (ch) 1) Proc saisir (ch)
2) Ecrire (FN conv_bin_dec(ch))
3) Fin conversion
b) Analyse de la procédure saisir
DEF PROC SAISIR (var ch : chaîne) Algorithme de la procédure saisir
Résultat = ch 0) DEF PROC SAISIR (var ch : chaîne)
1)Ch=[ ] répéter 1) répéter
Ch= donnée ("CH= ") Ecrire ("CH= "), lire (ch)
i0 i0
répéter répéter
ii+1 ii+1
test ch[i] dans ["0","1"] test ch[i] dans ["0","1"]
jusqu’à (non test) ou (i=long(ch)) jusqu’à (non test) ou (i=long(ch))
jusqu’à test Jusqu’à test
2) Fin saisir
c) Analyse de la fonction conv_bin_dec Algorithme de la fonction conv_bin_dec
DEF FN conv_bin_dec (ch :chaîne) : entier long
0)DEF FN conv_bin_dec (ch :chaîne): entire long
2)Résultat = conv_bin_dec n
1)N <- 0
1)N= [n0] pour i de 1 à long (ch) faire
pour i de 1 à long (ch) faire
N n +(ord(ch[i])-48)*puissance(long(ch)-i)
N n +(ord(ch[i])-48)*puissance(long(ch)-i)
Fin pour
Fin pour
2) conv_bin_dec N
3) Fin conv_bin_dec
d) Analyse de la fonction puissance Algorithme de la fonction puissance
DEF FN puissance (x :entier) :entier 0)DEF FN puissane (x :entier) : entier
2)Résultat = puissance p 1)p 1
Pour i de 1 à x faire
1)P=[ p 1] pour i de 1 à x Faire
Pp*2
P 2*p Fin pour
Fin pour 2)puissance p
3) Fin puissance
6](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-6-320.jpg)

![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
V. 5 Conversion d’un nombre hexadécimal en binaire
Activité : écrire un programme modulaire en pascal qui permet de saisir un nombre hexadécimal, le
convertit en binaire.
Analyse du programma principal :
2)Résultat= Ecrire("("ch," )16= (", FN conv_hex_bin(ch), ")2")
1)Ch= proc saisir (ch)
Algorithme du programme principal
TDOG 0) Début conversion
Objet Type/nature Rôle
1) proc saisir (ch)
Ch Chaîne
Saisir Procédure 2) Ecrire ("("ch,») 16= (", FN conv_hex_bin(ch), ")2")
Conv_hex_bin fonction 3 Fin conversion
Analyse de la procédure saisir
TDOL
DEF PROC saisir (var ch :chîne) Objet Type/nature Rôle
Résultat = ch i Entier
test booléen
1)Ch=[ ] répéter Algorithme de la procédure saisir
Ch= donnée ("CH=") 0) DEF PROC saisir (var ch :chîne)
i 0 1) répéter
Répéter Ecrire ("CH="), lire (ch)
i i+1 i 0
Répéter
ch[i] dans ["0".."9", "A".."F"]
i i+1
Jusqu’à (non test) ou (i=long (ch))
ch[i] dans ["0".."9", "A".."F"]
Jusqu’à (test)
jusqu’à (non test) ou (i=long(ch))
Analyse de la fonction conv_hex_bin Jusqu’à (test)
2) fin saisir
DEF FN conv_hex_bin (ch : chaîne): chaîne
2)Résultat= conv_hex_bin ph
2)Ph=[] tant que ph[1]= "0" faire TDOL
Efface(ph, 1, 1) Objet Type/nature Rôle
i Entier
Fin tant que con fonction
1)Ph=[ph""]pour i de 1 à long (ch) faire ph chaîne
Si ch[i] dans ["0".."9"] alors ph ph + conv(ord(ch[i])-48)
Sinon ph ph + conv (ord(ch[i])-55)
Fin si
Analyse de la fonction conv
DEF FN conv (x : entier): chaîne TDOL
2)Résultat= convdh Objet Type/nature Rôle
i Entier
1)dh=[dh"0000", i4] répéter dh chaîne
dh[i] chr((x mod 2)+48)
x x div 2
i i – 1
8](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-8-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
Algorithme de la fonction conv_hex_bin
jusqu’à (x=0)
0) DEF FN conv_hex_bin (ch : chaîne): chaîne Algorithme de la fonction conv
1) Ph"" 0) DEF FN conv (x : entier): chaîne
pour i de 1 à long (ch) faire 1) dh"0000"
Si ch[i] dans ["0".."9"] alors ph ph + conv(ord(ch[i])-48) i4
Sinon ph ph + conv (ord(ch[i])-55) répéter
Fin si dh[i] chr((x mod 2)+48)
2) tant que ph[1]= "0" faire x x div 2
Efface (ph, 1, 1) i i – 1
Fin tant que jusqu’à (x=0)
3) fin conv_hex_bin 2) fin conv
4) Fin conv_hex_bin
9](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-9-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
V. 6 Conversion d’un nombre binaire en hexadécimal
Activité : écrire un programme modulaire en pascal qui permet de saisir un nombre binaire, le
convertit en hexadécimal.
Analyse du programme principal :
2) Résulat= Ecrire ("(", ch, ") 2= (", FN conv_bin_hex(ch), ")16")
1) Ch= proc saisir (ch)
Algorithme du programme principal
TDOG
0) Début conversion
Objet Type/nature Rôle
Conv_bin_hex fonction 1) proc saisir (ch)
ch chaîne
2) Ecrire ("(", ch, ") 2= (", conv_bin_hex(ch), ")16")
Saisir procédure
3) Fin conversion
Analyse de la fonction conv_bin_hex
DEF FN conv_hex_bin (ch : chaîne): chaîne
3) Résultat= conv_bin_hex ph
2) Ph= [ph "" ] répéter
Ph ph + Fn conv (sous-chaîne (ch, 1, 4))
Efface (ch, 1, 4)
Algorithme de la fonction conv_bin_hex
Jusqu’à (long (ch)=0)
1) Ch=[ ] tant que long(ch) mod 4≠0 Faire 0) DEF FN conv_bin_hex (ch : chaîne): chaîne
Insère (ch, "0", 1) 1) tant que long(ch) mod 4≠0 Faire
Fin tant que Insère (ch, "0", 1)
Fin tant que
TDOL
2) ph ""
Objet Type/nature Rôle Répéter
conv fonction Ph ph + FN conv (sous-chaîne (ch, 1, 4))
ph chaîne Efface (ch, 1, 4)
Jusqu’à (long (ch)=0)
3) conv_bin_hex ph
Analyse de la fonction conv 4) fin conv_bin_hex
DEF FN conv (dh : chaîne) : caractère
Résultat= conv
2)Conv=[ ] si x dans [0..9] alors conv chr (x+48) Algorithme de la fonction conv
Sinon conv chr (x+55) 0) DEF FN conv (dh : chaîne) : caractère
Fin si 1) x0
pour i de 1 à 4 faire
1) x=[x0] pour i de 1 à 4 faire
x x + (ord (ch[i])-48) * FN puissance (4-i)
x x + (ord (ch[i])-48) * FN puissance (4-i)
Fin pour
Fin pour
2) si x dans [0..9] alors conv chr (x+48)
TDOL Sinon conv chr (x+55)
Objet Type/nature Rôle Fin si
x enier 3) Fin conv
i entier
10](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-10-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
Analyse de la fonction puissance Algorithme de la fonction puissance
DEF FN puissance (a :etier) : entier
Résultat=puissance b 0) DEF FN puissance (a :etier) : entier
1) b1
b=[b1] pour i de 1 à 4 faire
Pour i de 1 à 4 faire
bb*2
bb*2
fin pour
TDOL fin pour
Objet Type/nature Rôle 2) puissance b
b enier
i entier
11](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-11-320.jpg)
![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
V. 5 Conversion d’un nombre hexadécimal en décimal
Activité : écrire un programme modulaire en pascal qui permet de saisir un nombre hexadécimal, le
convertit en décimal.
Analyse du programme principal :
2) Résultat= Ecrire ("(ch",") 16= (", FN conv_hex_dec (ch),") 10")
1) Ch=proc saisir (ch)
Algorithme du programme principal TDOG
0) Début conversion Objet Type/nature
1) proc saisir (ch) saisir Procédure
Conv_hex_dec fonction
2) Ecrire ("(ch",") 16= (", FN conv_hex_dec (ch),") 10") ch chaîne
3) Fin conversion
Analyse de la fonction conv_hex_dec :
DEF FN conv_hex_dec (ch :chaîne): entire long
2) Résultat= conv_hex_dec N
1) N= [N 0] pour i de 1 à long (ch) faire
Si ch[i] dans ["0".."9"] alors N N + (ord (ch[i])-48) * FN puissance (long (ch) –i)
Sinon N N + (ord (ch[i])-55) * FN puissance (long (ch)-i)
Fin si
Fin pour
Algorithme de la fonction conv_hex_dec
0) DEF FN conv_hex_dec (ch :chaîne): entire long
1) N0
pour i de 1 à long (ch) faire TDOL
Si ch[i] dans ["0".."9"] alors N N + (ord (ch[i])-48) * FN puissance (long (ch) –i) Objet Type/nature
Sinon N N + (ord (ch[i])-55) * FN puissance (long (ch)-i) N Entier long
Fin si i entier
Fin pour
2) conv_hex_dec N
3) Fin conv_hex_dec
Analyse de la fonction puissance :
DEF FN puissance (x : entier) : entier long
2) Résultat= puissance p Algorithme de la fonction puissance
1) P= [p0] pour i de 1 à x faire 0) DEF FN puissance (x : entier) : entier long
P p * 16 1) p0
Fin pour Pour i de 1 à x faire
P p * 16
TDOL Fin pour
Objet Type/nature 2) Puissance p
p Entier long 3) Fin puissance
i entier
12](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-12-320.jpg)
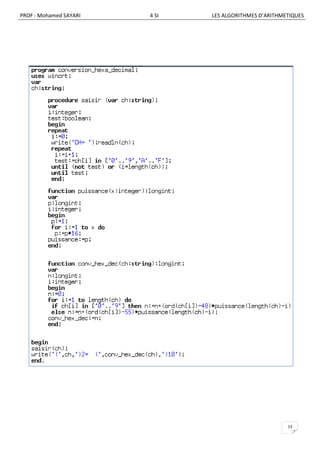

![PROF : Mohamed SAYARI 4 SI LES ALGORITHMES D’ARITHMETIQUES
b) Analyse de la fonction conversion
DEF FN conversion (ch : chaîne ; b1, b2 : entier) : chaîne
3) Résultat = conversion ph Algorithme de la fonction convesrion
2) Ph FN convb2 (n10, b2) 0) DEF FN conversion (ch : chaîne ; b1, b2 : entier)
1) N10 FN conv10 (ch, b1) 1) N10 FN conv10 (ch, b1)
2) Ph FN convb2 (n10, b2)
3) conversion ph
4) fin conversion
c) Analyse de la fonction conv10 (convertit un nombre vers la base décimal)
DEF FN conv10 (ch : chaîne ; b1 : entier) : entier long
2) Résultat= conv10 n
1) N= [n0] pour i de long (ch) à 1 (pas=-1) Faire
Si ch[i] dans ["0".."9"] alors n n + (ord (ch[i])-48) * Fn puissance (b1, long (ch)-1)
Sinon n n + (ord (ch[i])-55) * Fn puissance (b1, long (ch)-1)
Fin si
Fin pour
Algorithme de la fonction conv10
0) DEF FN conv10 (ch : chaîne ; b1 : entier) : entier long
1) n0
Pour i de long (ch) à 1 (pas=-1) Faire
Si ch[i] dans ["0".."9"] alors n n + (ord (ch[i])-48) * Fn puissance (b1, long (ch)-1)
Sinon n n + (ord (ch[i])-55) * Fn puissance (b1, long (ch)-1)
Fin si
Fin pour
2) conv10 n
3) Fin conv10
d) Analyse de la fonction convb2 (convertit un nombre décimal vers la base B2)
DEF FN convb2 (n1O : entier long ; b2 : entier) : chaîne
2) Résultat= convb2 ph
Algorithme de la fonction convb2
1) Ph= [ph""] répéter 0) DEF FN convb2 (n1O : entier long ; b2 : entier) : chaîne
R n mod b2 1) ph""
Si r ≤9 alors ph chr(r + 48) + ph Répéter
Sinon ph chr(r+55) + ph R n mod b2
Fin si Si r ≤9 alors ph chr(r + 48) + ph
Sinon ph chr(r+55) + ph
N10 N10 div b2 Fin si
Jusqu’à (N10 = 0) N10 N10 div b2
Jusqu’à (N10 = 0)
2) convb2 ph
3) fin convb2
Algorithme de la fonction puissance
e) Analyse de la fonction puissance 0) DEF FN puissance (x, y : entier) : entier long
DEF FN puissance (x, y : entier) : entier long 1) Z 1
2) Résultat= puissance Z Pour i de 1 à y faire
1) Z= [Z 1] pour i de 1 à y faire ZZ*x
Fin pour
ZZ*x
2) puissance Z
Fin pour 3) Fin puissance
15](https://image.slidesharecdn.com/lesalgorithmesdarithmetiques-120820133902-phpapp01/85/Les-algorithmes-d-arithmetique-15-320.jpg)
