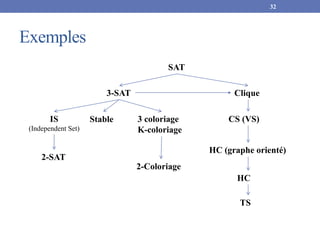
Le document traite de la complexité des problèmes algorithmique à travers des notions clés telles que la décidabilité, les classes P et NP, ainsi que les transformations polynomiales entre différents problèmes. Il détaille également les catégories de complexité en temps, y compris les machines de Turing déterministes et non déterministes, et explique des exemples de problèmes de décision et d'optimisation comme le problème du voyageur de commerce et la satisfiabilité booléenne (SAT). Enfin, le document aborde les notions de NP-complet et NP-dur en présentant des théorèmes et des exemples corollaires.

1. CHAPITRE 2 :
COMPLEXITÉ DES
PROBLÈMES
1

2. Introduction
• Problèmes décidables : la solution algorithmique existe
• Est-ce que cette solution est efficace ?
• Est-ce qu’elle utilise une quantité de ressources
« raisonnables »
temps et espace
2

3. Complexité des problèmes en temps
Principaux Facteurs
1. Machine (matériel et logiciel)
2. Données :
• Taille :
• Type :
• Valeurs :
• Organisation :
Paramètre principal n
À une constante près
Pas d’influence
Meilleur, moyenne et pire des cas
À une constante près
3

4. Complexité des problèmes en temps
La complexité en temps est calculée en fonction
de la taille des données n quand n est grand
(n  ∞) à un facteur près au pire des cas.
4

5. Exemple: Temps estimé en secondes
Taille des
données
O(Log n) O(n) O(n2) O(2n)
10
100
1000
10000
100000
3.10-6
7.10-6
10-5
13.10-6
17.10-6
10-5
10-4
10-3
10-2
10-1
10-4
10-2
1 sec
1,7 min
2,8 heures
10-3
1014 siècles
astronomique
..
..
5

6. Complexité D’une Machine De Turing
Déterministe
Définition 1
Soit M une machine de Turing Déterministe. La complexité en
temps de la machine M est la fonction TM (n) défini par :
TM (n) = max{ m, x  Ʃ* /|x|=n et M s’exécute sur x en m
étapes}
6

7. Complexité d’une machine de Turing
Non Déterministe
Définition 2
Le temps de calcul d’une machine de Turing non déterministe pour un
mot w noté TCM(w) est donné par :
 La longueur de la plus courte exécution acceptant le mot si w  L(M)
1 sinon
7

8. Complexité d’une machine de Turing
Non Déterministe
Définition 3
Soit M une machine de Turing non Déterministe. La
complexité en temps de la machine M est la fonction
TM (n) défini par :
TM (n) = max{ m, x  Ʃ* /|x|=n et m = TCM(x)}
8

9. Complexité des problèmes en temps
Définition Notation Asymptotique O
Une fonction g(n) est dite en O(f(n)) : g = O(f)
s’il existe une constante c, n0/pour tout n>n0 0≤g(n)≤c(f(n))
Proposition
Si la fonction f est calculée par une machine de Turing
non déterministe M avec la complexité TM(n) alors Ǝ une
machine de Turing non déterministe calculant f avec la
complexité O(C TM(n)) où C est une constante.
9

10. Complexité polynomiale en temps d’une
Machine de Turing
Définition 5
Une machine de Turing M est dite polynomiale en temps
s’il Ǝ un polynôme p(n) tel que TM(n)≤p(n) pour tout n≥0.
10

11. Complexité polynomiale en temps
d’une Machine de Turing
Définition 6: Classe P
La classe P est la classe des langages décidés par
une machine de Turing Déterministe Polynomiale
Définition 7: Classe NP
La classe NP est la classe des langages acceptés
par une machine de Turing Non Déterministe
Polynomiale
11

12. Complexité polynomiale en temps
d’une Machine de Turing
Théorème
Soit L  NP, Ǝ MTD M et un polynôme
p(n)/M décide de L avec la complexité
TM(n)=O(2p(n))
12

13. Problèmes de décisions
• Un problème est dit de décision si pour tout input, l’unique
output possible est de type booléen.
• La plupart des problèmes d’optimisation peuvent être convertis à
des problèmes de décision.
• Il suffit d’ajouter une borne k sur la valeur à optimiser et changer
la question :
• Existe-t-il une solution dont la valeur est au plus k (en cas de minimisation);
• Existe-t-il une solution dont la valeur est au moins k (en cas de
maximisation).
13

14. Problèmes de décisions :Exemples
Circuit Hamiltonien
Étant donné un graphe G, existe-t-il un chemin de longueur au plus k ?
Voyageur de commerce TSP
Étant donné un ensemble de villes 𝑉 = {𝑣1, … , 𝑣𝑛} et une fonction distance
𝑑(𝑣𝑖, 𝑣𝑗) entre les villes, et soit un nombre k.
Existe-t-il un tour de toutes les villes dont la longueur au plus k ?
14
v1
v5
v3
v2
v4
d(v1,v2)

15. Transformation Polynomiale
Définition 8
Soient L1 ∈ Ʃ1
* et L2 ∈ Ʃ2
*
Une transformation polynomiale de L1 vers
L2 noté L1 α L2 est une fonction f définie par
f: Ʃ1
*  Ʃ2
* tel que:
1. f est calculable en un temps polynomial
2. f(x)  L2 ssi x  L1
15

16. Propriétés des Transformations
Polynomiales
Lemme 1
Si L1 α L2 alors
1. Si L2  P alors L1  P
2. Si L1  P alors L2  P
16
Lemme 2 Transitivité de la transformation polynomiale
Si L1 α L2 et L2 α L3 alors L1 α L3

17. Transformation polynomiale
1. Transformation en temps polynomial,
2. Si la fonction F peut être calculer en temps polynomial, on dit
que L1 est polynomialement réductible a L2, et on note L1 α L2
17
Problème L1
Input X
Problème L2
Input F(X)
Algorithme
Transformation F
L1 L2
x
F(x)
Transformation Polynomiale
= Projection = Réduction

18. Equivalence polynomiale
Définition 9
Deux langages L1 et L2 sont équivalents polynômialement notée ≡P
L1 ≡P L2 ssi L1 α L2 et L2 α L1
Définition 10
Une classe d’équivalence polynomiale C1 est inférieure à une classe
d’équivalence C2 noté C1 ≼ C2 Si :
 L1  C1 et  L2  C2 on a L1 α L2
S’il existe une transformation polynomiale de tout langage de C1 vers tout
langage C2 , on note C1 ≼p C2
18

19. Propriétés des Transformations
Polynomiales
Lemme 3
La classe P est une classe d’équivalence
polynomiale.
19
Lemme 4
Pout tout L1  Pet  L2  NP on a L1 α L2
P ≼ c  c classe d’équivalence de NP.

20. Propriétés des Transformations
Polynomiales
Définition
L est NP-Dûr si  L’  NPC alors L’ α L.
20
Exemple
Problème d’équivalence d’automates à état finie non
déterministe est NP-Dûr.

21. Problème NP-Complet
Définition 11
L est dit NP-complet (NPC) si
1. L  NP
2.  L’  NP on a L’ α L
21

22. Problème NP-Complet
Définition 12
L est dit NP-complet (NPC) si
1. L  NP
2.  L’  NPC alors L’ α L
22

23. Problème NP-Complet
Démonstration : par transitivité 2‘2
L  NPC
L  NP L’ α L avec L’  NPC
L’  NP ,  L''  NP alors (par transitivité) L'' α L' et L' α L
  L''  NP et L'' α L
23

24. Premier Problème NP-Complet
Théorème de COOK
SAT  NPC
24

25. Théorème de COOK
Démonstration
1) SAT  NP
2)  L'  NP alors L' α SAT
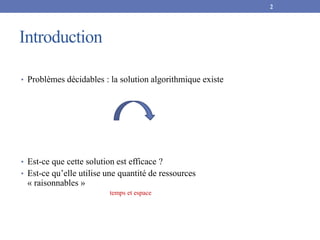
25
Pour montrer que SAT  NP
a- Soit une interprétation I de façon
non déterministe;
b- Vérifier que [𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛
Données de SAT
𝑃 = 𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛
𝐹 =∧𝑖=1
𝑛
𝐴𝑖
𝐴𝑖 =∨𝑗=1
𝑘𝑖
𝐿𝑖𝑗
[𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛
Algorithme ND
𝐼 = 𝑛
𝑜𝑛 𝑎 𝑚 𝑐𝑙𝑎𝑢𝑠𝑒𝑠
𝑝𝑜𝑢𝑟 𝑢𝑛𝑒 𝑐𝑙𝑎𝑢𝑠𝑒 𝐴𝑖
𝑘 = max
1≤𝑖≤2𝑛
𝑘𝑖; le nombre littéraux
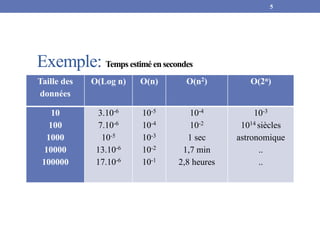
p=max(n, m, k) 𝑂(𝑝3)
Polynomial : SAT  NP

26. Les classes P et NP
26
P NP-Complet
NP-Dur
NP-Difficile
NP
SAT TSP
CH PLC
k-SAT
Tri
2-SAT
2-COL
PCC
Vérifiabilité polynomiale
Résolution
polynomiale

27. SAT
• Un problème fondamental en théorie de la complexité,
• Satisfiabilité booléenne des formules de la logique
propositionnelle,
• C’est le premier problème NP-découvert (Théorème de Cook, 1971),
• Solveur SAT (exemple: logictools.org)
27

28. SAT : description d’un problème
• Valeurs booléennes Vrai et Faux : ⊺, ⊥
• Variables booléennes : par exemple: a, b, c, d;
• Formule: F = F (a, b, c, d)
• Variables =?  eval (F)= ⊺
• Si affectation possible, F est SATisfiable,
• Si non, inSATisfiable.
28

29. SAT : description d’un problème
Nature de la formule
• 𝑭 = (𝑎 ∨ ¬𝑐 ∨ 𝑑) ∧ (¬𝑎 ∨ ¬𝑏) ∧ (¬𝑎 ∨ ¬𝑐) ∧ 𝑏 ∨ ¬𝑑 ∧ 𝑏 ∨ 𝑐 ∨ 𝑑
𝐶1
• F est sous forme normale conjonctive (CNF)
• F est conjonction : 𝐶1 ∧ 𝐶2 ∧ ⋯ ∧ 𝐶𝑘
• Chaque 𝐶𝑖 est une clause:
• 𝐶𝑖 est une disjonction de littéraux : 𝑙1 ∨ 𝑙2 ∨ ⋯ ∨ 𝑙𝑝;
• Chaque opérant de la disjonction est un littéral 𝑙𝑗 : de la forme variable propositionnelle ou sa
négation 𝑣 et ¬𝑣;
• CNF non restrictif;
• Affectation rend F satisfiable ( chaque clause s’évalue à T):
• 𝑎 = ⊥
• 𝑏, 𝑐, 𝑑 = ⊺
29

30. SAT : description d’un problème
Nature de la formule
𝑭 = (𝑎 ∨ ¬𝑐 ∨ 𝑑) ∧ (¬𝑎 ∨ ¬𝑏) ∧ (¬𝑎 ∨ ¬𝑐) ∧ 𝑏 ∨ ¬𝑑 ∧ 𝑏 ∨ 𝑐 ∨ 𝑑
• F est une formule cohérente,
• Interprétation : assignation d’une valeur de vérité à chaque
variable I: {a=faux, b=Vrai, c=vrai, d=Vrai},
• Modèle d’une formule F : interprétation pour laquelle F a la
valeur Vrai,
• Formule F cohérente : F admet au moins un modèle.
30

31. Exemple : Problème SAT
31
I= (𝑎 ∨ 𝑏 ∨ 𝑐) ∧ (¬𝑎 ∨ 𝑏) ∧ ¬𝑐
….
J= (𝑎 ∨ 𝑏 ∨ 𝑐) ∧ (¬𝑎 ∨ 𝑏) ∧
¬𝑐 ∧ ¬𝑏 Vrai
Faux
Vérificateur
S= {a=Vrai, b=Vrai, c=Faux},
…
{a=Faux, b=Faux, c=Vrai},
Instance de SAT
Certificat de I

32. Exemples
32
SAT
3-SAT Clique
3 coloriage
K-coloriage
CS (VS)
HC (graphe orienté)
HC
TS
Stable
IS
(Independent Set)
2-SAT
2-Coloriage

33. 3-SAT : Description d’un problème
Nature de la formule
• Soit F est conjonction : 𝐹 = 𝐶1 ∧ 𝐶2 ∧ ⋯ ∧ 𝐶𝑘 une formule en 3-CNF, avec k
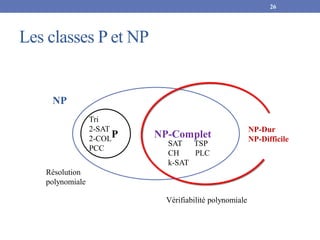
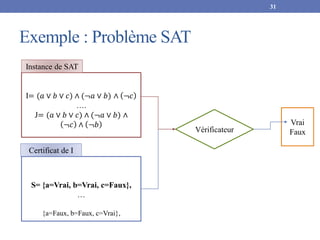
clauses, contenant chacune 3 littéraux distincts.
• Pour chaque clause on crée 3 sommets, un pour chaque littéral dans la clause.
Données :
𝑃 = 𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛
𝐹 =∧𝑖=1
𝑛
𝐴𝑖 𝑜𝑢 𝐹 = {𝐴𝑖; 1 ≤ 𝑖 ≤ 𝑛} avec 𝐴𝑖 =∨𝑗=1
3
𝐿𝑖𝑗.
(𝐴𝑖 𝑙′
𝑒𝑛𝑠𝑒𝑚𝑏𝑙𝑒 𝑑𝑒 𝑐𝑙𝑎𝑢𝑠𝑒𝑠 𝑒𝑡 3 𝑙𝑖𝑡𝑡é𝑟𝑎𝑢𝑥 𝑝𝑎𝑟 𝑐𝑙𝑎𝑢𝑠𝑒)
Problème :
Existe-t-il une interprétation I / [𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛 ?
33

34. Circuit Hamiltonien : Description d’un problème
Données :
Soit un graphe G = (S, A) et |S|=n sommets.
Problème :
Existe-t-il un parcours fermé qui passe par tous les sommets une
seule fois?
Trouver une permutation 𝑠𝑝1, … , 𝑠𝑝𝑛 𝑑𝑒 𝑆,
𝑒𝑡 (𝑠𝑝𝑖, … , 𝑠𝑝𝑖+1) ∈ 𝐴 ∀ 1 ≤ 𝑖 ≤ 𝑛 − 1; (𝑠𝑝𝑛 , … , 𝑠𝑝1) ∈ A.
34
G=(S,A)
5
4
3 2
1

35. Voyageur de commerce (TSP) : Description d’un
problème
Données :
Soit un graphe G = (V, E) complet et pondéré avec V l’ensemble de
villes, et 𝑑(𝑣𝑖, 𝑣𝑗) : la distance entre ville i et ville j et un entier 𝑏.
Problème :
Existe-t-il un parcours fermé qui passe par toutes les villes une seule
fois dont la longueur ≤ 𝑏?
Trouver une permutation 𝑣𝑝1, … , 𝑣𝑝𝑛 𝑑𝑒 𝑉,
𝑒𝑡
𝑖=1
𝑛−1
𝑑 (𝑣𝑝𝑖, … , 𝑣𝑝𝑖+1)+ 𝑑(𝑣𝑝𝑛, … , 𝑣𝑝1) ≤ 𝑏
35

36. Exemples : Circuit Ham𝑖𝑙𝑡𝑜𝑛𝑖𝑒𝑛 ∝ TSP
Exercice :
Montrer que CH ∝ 𝑇𝑆𝑃.
36
CH
Input G=(S,A)
TSP ou n=|V|
Input F(X)=G'=(V, E)
Algorithme
Transformation F
5
4
3 2
1
5
4
3 2
1
1
1
1
1
1
1
1
2
2
2
Définition de F :
V=S
𝑑(𝑣𝑖, … , 𝑣𝑗) =
1 𝑠𝑖 (𝑣𝑖, … , 𝑣𝑗) ∈ 𝐴
2 𝑠𝑖 𝑛𝑜𝑛
b= |V|=n

37. Cliques Maximale : Description d’un problème
Données :
graphe G = (S, A) et un entier 𝑘 ≤ |𝑆|
Problème :
G contient-il une clique de taille k?
Existe-t-il un sous-graphe complet dont le nombre de sommet ≥ 𝑘?
∃ 𝑆′ ⊂ 𝑆 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′ ≥ 𝑘
∀ 𝑠1 ∈ 𝑆′
𝑒𝑡 𝑠2 ∈ 𝑆′
on a (𝑠1, 𝑠2 ) ∈ A
37

38. Couverture par Sommet (Vertex Code) : Description
d’un problème
Données :
Graphe G = (S, A) et un entier 𝑘 ≤ |𝑆|
Problème :
Existe-t-il une couverture par sommets de G de taille k?
∃ 𝑆′
⊂ 𝑆 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
≤ 𝑘
∀ (𝑠1, 𝑠2 ) ∈ A on a 𝑠1 ∈ 𝑆′ 𝑜𝑢 𝑠2 ∈ 𝑆′
38

39. Coloration de Graphe : Description d’un problème
Données :
Un graphe G = (S, A) et un entier 𝑘 ≤ |𝑆|
Problème :
Existe-t-il une coloration des sommets de G de taille k (k couleurs)?
Existe-t-il une coloration minimale de telle sorte que deux sommets
adjacents seront coloriés avec deux couleurs différentes?
39

40. Exemples : Coloration de Graphe
40
3-coloriage
3-coloriage
Vrai
Faux
Graphe G
Vrai
Faux
Vérificateur
S= {V,B,O,V,O},
…
S‘={V,B,V,V,O},
Instance de Coloration de Graphe
Certificat de I
k=3 k=3
Instance
Positive
Certificat
Positif
Instance
Négative

41. Exemple : Transformation Polynomiale
Coloration de Graphe ∝ 𝑆𝐴𝑇
SAT
• Données : les formules
propositionnelles au format
CNF.
• Problème : Trouver les
formules CNF Cohérentes.
41
Coloration de Graphe
• Données : un graphe G non
orienté et un entier k.
• Problème : Coloration d’un
graphe avec au moins k
couleurs.
Algorithme
Transformation
b c
a
Transformation
𝑭 = {𝑎, 𝑏, 𝑐, ¬𝑎, ¬𝑏, ¬𝑐/∧,∨}

42. Le plus long Cycle (PLC) : Description d’un problème
Données :
Soit un graphe G = (S, A) et un entier 𝑘.
Problème :
Déterminer si G possède un cycle de longueur ≥ 𝑘.
Exercice :
Montrer que CH ∝ 𝑃𝐿𝐶.
42
CH
Input G=(S,A)
PLC
Input F(X)=G'=(S',A')
Algorithme
Transformation F

43. Somme de sous-ensemble : Description d’un problème
Données :
𝑆 ⊆ ℕ 𝑒𝑡 𝑡 ∈ ℕ
Problème :
Existe-t-il 𝑆′ ⊆ 𝑆 / 𝑠𝑖
′∈𝑆′ 𝑠𝑖
′
= 𝑡 ?
Exemple :
S= {1, 3 , 5, 45, 65, 98, 45658, 45458, 1235, 785, 659}
t=1590,
43

44. Exercice 1
Prouver que
𝑇𝑆𝑃 ∝ 𝐶ircuit Hamiltonien et
𝐶ircuit Hamiltonien ∝ 𝑇𝑆𝑃
44

45. Exercice 2
Prouver que
𝐶𝑙𝑖𝑞𝑢𝑒 𝑀𝑎𝑥𝑖𝑚𝑎𝑙𝑒
∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡.
45

46. Correction Exercice 2 :𝐶𝑙𝑖𝑞𝑢𝑒 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒𝑆𝑜𝑚𝑚𝑒𝑡
Données :
Graphe 𝐺1 = ( 𝑆1, 𝐴1), | 𝑆1|=n
et un entier 𝑘1≤ | 𝑆1|
Problème :
G contient-il une clique de taille
𝑘1?
Existe-t-il un sous-graphe complet
dont le nombre de sommet ≥ 𝑘1?
∃ 𝑆′
1 ⊆ 𝑆1 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
1 ≥ 𝑘1 et
∀ 𝑠1∈ 𝑆′
1 𝑒𝑡 𝑠2 ∈ 𝑆′
1
𝑎𝑙𝑜𝑟𝑠 (𝑠1, 𝑠2 ) ∈ 𝐴1
46
Données :
Graphe 𝐺2 = ( 𝑆2, 𝐴2) et un entier
𝑘2 ≤ | 𝑆2|
Problème :
Existe-t-il une couverture par
sommets de G de taille 𝑘2?
∃ ? 𝑆′
2 ⊆ 𝑆2 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
2 ≤ 𝑘2 et
∀ (𝑠1, 𝑠2 ) ∈ 𝐴2 on a 𝑠1 ∈ 𝑆′
2
𝑜𝑢 𝑠2 ∈ 𝑆′
2
𝑪𝒐𝒖𝒗𝒆𝒓𝒕𝒖𝒓𝒆 𝒅𝒆 𝑺𝒐𝒎𝒎𝒆𝒕
𝑪𝒍𝒊𝒒𝒖𝒆

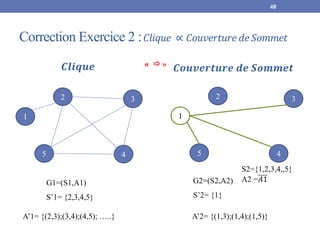
47. Correction Exercice 2 :𝐶𝑙𝑖𝑞𝑢𝑒 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒𝑆𝑜𝑚𝑚𝑒𝑡
47
Montrer que f est calculable en un temps polynomial :
Algorithme:
Pour i de 1 à n faire
𝑆2[𝑖] = 𝑆1[𝑖]
Fin pour
Pour i de 1 à n faire
Pour j de 1 à n faire
Si 𝑠𝑖, 𝑠𝑗 ∉ 𝐴1𝑒𝑡 (𝑖 ≠ 𝑗) alors
𝐴2 = 𝐴2 ∪ (𝑠𝑖, 𝑠𝑗)
Fin Si
Fin pour
Fin pour
𝑘2 = 𝑛 − 𝑘1
Pour i de 1 à n faire
Si (𝑠𝑖∉ 𝑆′1) alors
𝑆′2 = 𝑆′2 ∪ {𝑠𝑖}
Fin Si
Fin Pour
O(n)
O(n2)
La transformation est de O(n2)
 Transformation polynomiale
 f est calculable en un temps
polynomial et borné par O(n2).
O(1)
O(n)
𝐴2 = 𝐴1 = { 𝑠1, 𝑠2 ∉ 𝐴1}
𝑆2 = 𝑆1
𝑘2 = |𝑆1| − 𝑘1 = 𝑛 − 𝑘1
𝑆′2 = 𝑆1𝑆′1
Calcule de
la solution

48. 48
2
1
5 4
3
G1=(S1,A1)
S’1= {2,3,4,5}
A’1= {(2,3);(3,4);(4,5); …..}
2
1
5 4
3
G2=(S2,A2)
S’2= {1}
A’2= {(1,3);(1,4);(1,5)}
Correction Exercice 2 :𝐶𝑙𝑖𝑞𝑢𝑒 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒𝑆𝑜𝑚𝑚𝑒𝑡
𝑪𝒐𝒖𝒗𝒆𝒓𝒕𝒖𝒓𝒆 𝒅𝒆 𝑺𝒐𝒎𝒎𝒆𝒕
𝑪𝒍𝒊𝒒𝒖𝒆 «  »
A2 =𝐴1
S2={1,2,3,4,,5}

49. Correction Exercice 2 :𝐶𝑙𝑖𝑞𝑢𝑒 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒𝑆𝑜𝑚𝑚𝑒𝑡
49
”  »
Soit x ∈ 𝐶𝑙𝑖𝑞𝑢𝑒  Montrer que f(x) ∈ 𝐶𝑆
∃ 𝑆′
1 ⊆ 𝑆1 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
1 ≥ 𝑘1 et ∀ 𝑠1∈ 𝑆′
1 𝑒𝑡 𝑠2 ∈ 𝑆′
1alors
(𝑠1, 𝑠2 ) ∈ 𝐴1
o𝑛 𝑎 𝑆′
2 = 𝑆1 ∖ 𝑆′
1 = 𝑆2 ∖ 𝑆′
1 ⊆ 𝑆2
𝑆2 = 𝑆2| − |𝑆′
1
𝑆2 ≤ 𝑛 − 𝑘1 = 𝑘2
∀(𝑠1, 𝑠2 ) ∈ 𝐴2 𝑎𝑙𝑜𝑟𝑠 (𝑠1, 𝑠2 ) ∉ 𝐴1 𝑑𝑜𝑛𝑐 𝑠1 ∉ 𝑆′
1𝑜𝑢 𝑠2 ∉ 𝑆′
1
 𝑠1 ∈ 𝑆2 𝑜𝑢 𝑠2 ∈ 𝑆2
𝑫𝒐𝒏𝒄 𝑺′
𝟐 𝒆𝒔𝒕 𝒖𝒏𝒆 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏 𝒅𝒆 CS

50. Correction Exercice 2 :𝐶𝑙𝑖𝑞𝑢𝑒 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒𝑆𝑜𝑚𝑚𝑒𝑡
50
”  ”
Soit f(x) ∈ 𝐶𝑆  Montrer que x ∈ 𝐶𝑙𝑖𝑞𝑢𝑒
∃ 𝑆′
2 ⊆ 𝑆2 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
2 ≤ 𝑘2 et ∀(𝑠1, 𝑠2 ) ∈ 𝐴2 alors
on a 𝑠1 ∈ 𝑆′
2 𝑜𝑢 𝑠2 ∈ 𝑆′
2
o𝑛 𝑎 𝑆′
1 = 𝑆1 ∖ 𝑆′
2 = 𝑆2 ∖ 𝑆′
2 ⊆ 𝑆1
|𝑆′
1| = 𝑆2 ∖ 𝑆′
2 = 𝑆2| − |𝑆′
2 ≥ 𝑛 − 𝑘2 = 𝑘1
∀ 𝑠1∈ 𝑆′
1 𝑒𝑡 𝑠2 ∈ 𝑆′
1  ∀ 𝑠1∉ 𝑆′
2 𝑒𝑡 𝑠2 ∉ 𝑆′
2
(𝑠1, 𝑠2 ) ∉ 𝐴2= 𝐴1  (𝑠1, 𝑠2 ) ∈ 𝐴1
𝑫𝒐𝒏𝒄 𝑺′
𝟏 𝒆𝒔𝒕 𝒖𝒏𝒆 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏 𝒅𝒆 𝑪𝒍𝒊𝒒𝒖𝒆 𝒆𝒕 𝒙 ∈ 𝑪𝒍𝒊𝒒𝒖𝒆
𝒇 𝒙 ∈ 𝑪𝑺
D’où 𝑪𝒍𝒊𝒒𝒖𝒆 ∝ 𝑪𝑺

51. Exercice 3
Prouver que
3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡.
51

52. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
Indication :
1. Toute variable propositionnelle on lui associe 2 sommets (variable et sa
négation) Exemple : p → 𝑝 𝑒𝑡 ¬𝑝;
2. Toute clause est représentée par un triangle étiqueté par 3 littéraux de clauses;
3. Une arête est couverte par 1 sommet et un triangle est couvert par 2 sommets.
52
Prouver que : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡.
3-SAT
Données :
𝑃 = 𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛
𝐹 =∧𝑖=1
𝑚
𝐴𝑖
𝐴𝑖 =∨𝑗=1
3
𝐿𝑖𝑗
Problème :
Existe-t-il une interprétation I /
[𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛 ?
𝑪𝒐𝒖𝒗𝒆𝒓𝒕𝒖𝒓𝒆 𝒅𝒆 𝑺𝒐𝒎𝒎𝒆𝒕
Données :
𝐺: 𝑆, 𝐴
Problème :
Existe-t-il une couverture par
sommets de G de taille k?
∃ 𝑆′
⊆ 𝑆 𝑡𝑒𝑙𝑞𝑢𝑒 |𝑆′
| ≤ 𝑘 et
∀ (𝑠1, 𝑠2 ) ∈ A
on a 𝑠1 ∈ 𝑆′
𝑜𝑢 𝑠2 ∈ 𝑆′
Transformation
F(x)

53. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
𝑩 = (𝑝1 ∨ 𝑝2 ∨ 𝑝3) ∧ (𝑝1 ∨ ¬𝑝2 ∨ 𝑝4) ∧ 𝑝2 ∨ ¬𝑝3 ∨ ¬𝑝4
53
 l’algorithme de transformation est polynomiale ≅ O(n2)
car on a la taille de graphe est 2n+3m d’où pour parcourir les sommets
on a [2n+3m]2 ≅O(n2).
𝑝1 ¬𝑝1 𝑝2 ¬𝑝2 𝑝3 ¬𝑝3 𝑝4 ¬𝑝4
𝑙1
1
𝑙2
1
𝑙3
1
𝑙1
2 𝑙2
2
𝑙3
2
𝑙1
3
𝑙2
3
𝑙3
3
n variables et
m clauses 
la taille de
graphe est
2n+3m
La taille de CS :
 k=2m+n (nombre de sommets couverts)
n : pour la couverture de tout les sommets 𝑝𝑖 𝑜ù 𝑝𝑖 𝐼 =V,
2m : pour couvrir les arêtes de chaque triangle.
𝑝1 ¬𝑝1 𝑝2 ¬𝑝2 𝑝3 ¬𝑝3 𝑝4 ¬𝑝4
𝑉 𝐹
𝑉 𝑉
𝑝1 𝐼 = 𝑝2 𝐼 = 𝑝4 𝐼 = 𝑉
𝑒𝑡 𝑝3 𝐼 = 𝐹

54. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
k= 2n+3m
𝑆 = 𝑆1 ∪ 𝑆2
𝑆1 = 𝑝𝑖, ¬𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛 ; 𝑆1 = 2𝑛
𝑆2 = 𝐿𝑖1, 𝐿𝑖2, 𝐿𝑖3; 1 ≤ 𝑖 ≤ 𝑚 ; 𝑆2 = 3𝑚
𝐴𝑖 =∨𝑖=1
3
𝐿𝑖𝑗
𝑺 = 𝟐𝒏 + 𝟑m
54
Prouver que : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡.
𝐴 = 𝐴1 ∪ 𝐴2∪ 𝐴3
𝐴1 = 𝑝𝑖, ¬𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛 ; 𝐴1 = 𝑛
𝐴2 = (𝐿𝑖1, 𝐿𝑖2); (𝐿𝑖1, 𝐿𝑖3); 𝐿𝑖2, 𝐿𝑖3 ; 1 ≤ 𝑖 ≤ 𝑚; 𝐿𝑖𝑗 ∈ 𝑆2 ; 𝐴2 = 3𝑚
𝐴3 = (𝐿𝑖𝑗, 𝑋𝑘); (𝐿𝑖𝑗 ∈ 𝑆2 ); 𝑝𝑘 ∈ 𝑆1 ; 𝐿𝑖𝑗 ∈ 𝑋𝑘, 𝑎𝑣𝑒𝑐 𝑋𝑘 = 𝑝𝑘 𝑜𝑢 ¬𝑝𝑘 ; 𝐴3 = 3𝑚
𝑨 = 𝒏 + 𝟑𝒎 + 𝟑𝒎 = 𝒏 + 𝟔𝒎

55. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
55
Prouver que : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡.
Montrer que f est calculable en un temps polynomial :
Algorithme:
Pour i de 1 à n faire
𝑆1 = 𝑆1 ∪ 𝑝𝑖, ¬𝑝𝑖
Fin pour
Pour i de 1 à m faire
𝑆2 = 𝑆2 ∪ 𝐿𝑖1, 𝐿𝑖2, 𝐿𝑖3
Fin pour
𝑆 = 𝑆1 ∪ 𝑆2
O(n)
O(m)
O(2n+3m): parcours de tous les sommets
l= max
(m,n)
O(l)
k= 2n+3m
𝑆 = 𝑆1 ∪ 𝑆2
𝑆1 = 𝑝𝑖, ¬𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑛 ; 𝑆1 = 2𝑛
𝑆2 = 𝐿𝑖1, 𝐿𝑖2, 𝐿𝑖3; 1 ≤ 𝑖 ≤ 𝑚 ; 𝑆2 = 3𝑚
𝐴𝑖 =∨𝑖=1
3
𝐿𝑖𝑗
𝑺 = 𝟐𝒏 + 𝟑m

56. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
56
Algorithme (suite):
Pour i de 1 à n faire
𝐴1 = 𝐴1 ∪ 𝑝𝑖, ¬𝑝𝑖
Fin pour
Pour i de 1 à m faire
𝐴2 = 𝐴2 ∪ (𝐿𝑖1,𝐿𝑖2); (𝐿𝑖1,𝐿𝑖3); 𝐿𝑖2, 𝐿𝑖3
Fin pour
Pour i de 1 à m faire
Pour j de 1 à 3 faire
Pour k de 1 à n faire
si (𝐿𝑖𝑗= 𝑝𝑘) alors 𝐴3 = 𝐴3 ∪ (𝐿𝑖𝑗, 𝑝𝑘)
si non si (𝐿𝑖𝑗= ¬𝑝𝑘) alors 𝐴3 = 𝐴3 ∪ (𝐿𝑖𝑗, ¬𝑝𝑘)
Fin si
Fin Pour
Fin Pour
Fin pour
𝐴 = 𝐴1 ∪ 𝐴2 ∪ 𝐴3;
k= n+2m
Fin algorithme
O(n)
O(m)
O(nm)
O(l2)
O(n+6m)
 O(l2)
D’où f est calculable en un
temps polynomiale
𝐴 = 𝐴1 ∪ 𝐴2∪ 𝐴3
𝐴1 = 𝑛 ; 𝐴2 = 3𝑚; 𝐴3 = 3𝑚
𝑨 = 𝒏 + 𝟑𝒎 + 𝟑𝒎 = 𝒏 + 𝟔𝒎
O(1)

57. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
• x ∈ 3𝑆𝐴𝑇  Montrer que f(x) ∈ 𝐶𝑆
∃ ? 𝑆′
⊂ 𝑆 𝑡𝑒𝑙𝑞𝑢𝑒 𝑆′
𝑒𝑠𝑡 𝑢𝑛𝑒 𝑐𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒
∃ ? I / [𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑚
∃ ? 𝑗0 / [𝐴𝑖𝑗0]𝐼=V
𝑝𝑖 ∈ 𝑃 ; 𝑠𝑖 𝑝𝑖 = 𝑉 𝑝𝑖 ∈ 𝑆′
𝑠𝑖 𝑝𝑖 = 𝐹 ¬𝑝𝑖∈ 𝑆′
∀ 𝑖 𝐿𝑖𝑗1, 𝐿𝑖𝑗2 ∈ 𝑆′
tel que 𝑗1 𝑒𝑡𝑗2 ≠ 𝑗0
|𝑆′
| = 𝑛 + 2𝑚 = 𝑘 𝑜𝑢 ≤ 𝑘
57
1
2
𝑺′
𝒆𝒔𝒕 𝒖𝒏𝒆 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏 𝒅𝒆 𝑪𝑺

58. Exercice 3 : 3𝑆𝐴𝑇 ∝ 𝐶𝑜𝑢𝑣𝑒𝑟𝑡𝑢𝑟𝑒 𝑑𝑒 𝑆𝑜𝑚𝑚𝑒𝑡
Prouvons : ∀ 𝑠1, 𝑠2 ∈ 𝐴 𝑎𝑙𝑜𝑟𝑠 𝑠1 ∈ 𝑆′ 𝑜𝑢 𝑠2 ∈ 𝑆′
𝑠1, 𝑠2 ∈ 𝐴1 ∃ I / 𝑠1, 𝑠2 = 𝑝𝑖, ¬𝑝𝑖
𝑝𝑖 ∈ 𝑆′
ou ¬𝑝𝑖∈ 𝑆′
 𝐴1 est couvert
𝑠1, 𝑠2 ∈ 𝐴2 : 𝑠1, 𝑠2 = (𝐿𝑖1, 𝐿𝑖2) ou (𝐿𝑖1, 𝐿𝑖3) ou (𝐿𝑖2, 𝐿𝑖3)
𝐿𝑖𝑗1, 𝐿𝑖𝑗2 ∈ 𝑆′
O𝑛 𝑎 𝑠1 ∈ 𝑆′
ou 𝑠2 ∈ 𝑆′
𝐴𝟐 est couvert
𝑠1, 𝑠2 = (𝐿𝑖𝑗1, 𝑥𝑘) ou (𝐿𝑖𝑗2, 𝑥𝑘) ou (𝐿𝑖𝑗3, 𝑥𝑘)
[𝐿𝑖𝑗0]𝐼=V  𝑥𝑘 𝐼= V
𝐴𝟑 est couvert
58
D’après 1 :
 𝑫′
𝒐ù 𝑨 est couvert
 𝑺′
𝒆𝒔𝒕 𝒖𝒏𝒆 𝒔𝒐𝒍𝒖𝒕𝒊𝒐𝒏 𝒅𝒆 𝑪𝑺
D’après 2 :
D’après 2 : car
𝐿𝑖𝑗1 ∈ 𝑆′ et 𝐿𝑖𝑗2 ∈ 𝑆′
D’après 1 et 2 : 𝑥𝑘 ∈ 𝑆′

59. Exercice 4
Prouver que 3𝑆𝐴𝑇 ∈ 𝑁𝑃𝐶,
sachant que 𝑆𝐴𝑇 ∈ 𝑁𝑃𝐶.
59

60. Exercice 4 : Correction
Prouver que ∶
3𝑆𝐴𝑇 ∈ 𝑁𝑃𝐶, sachant que 𝑆𝐴𝑇 ∈ 𝑁𝑃𝐶.
60
1) 3SAT est un cas particulier de SAT ∈ 𝑁𝑃 (avec k=3) donc 3SAT ∈ 𝑁𝑃.
2)
SAT
Données :
𝑃 = 𝑝𝑖; 1 ≤ 𝑖 ≤ 𝑚
𝐹 =∧𝑖=1
𝑛
𝐴𝑖
𝐴𝑖 =∨𝑗=1
𝑘𝑖
𝐿𝑖𝑗
Problème :
Existe-t-il une interprétation I /
[𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛 ?
3 SAT
Données :
𝑃′ = 𝑝′𝑖; 1 ≤ 𝑖 ≤ 𝑚′
𝐹′ =∧𝑖=1
𝑛′
𝐴′𝑖
𝐴′𝑖 =∨𝑗=1
3
𝐿′𝑖𝑗
Problème :
Existe-t-il une interprétation I' /
[𝐴′𝑖]𝐼′=V ∀ 1 ≤ 𝑖 ≤ 𝑛' ?
𝑘𝑖 = 3 ; 𝐴′𝑖 = 𝐴𝑖;
𝑘𝑖 = 2 ; 𝐴𝑖 = 𝑥1 ∨ 𝑥2 ; 𝑓(𝐴𝑖) = 𝐴′𝑖 = (𝑥1 ∨ 𝑥2∨ 𝑦1) ∧ (𝑥1 ∨ 𝑥2∨ ¬𝑦1);
𝑘𝑖 = 1 ; 𝐴𝑖 = 𝑥1; 𝑓(𝐴𝑖) = 𝐴′𝑖= (𝑥1 ∨ 𝑥2∨ 𝑦1) ∧ (¬𝑦1 ∨ 𝑥3∨ 𝑦2) ∧
¬𝑦2 ∨ 𝑥4∨ 𝑦3 … ∧ (¬𝑦𝑝−4 ∨ 𝑥𝑝−2∨ 𝑦𝑝−3) ∧ (¬𝑦𝑝−3 ∨ 𝑥𝑝−1∨ 𝑥𝑝);

61. Exercice 4 : Correction
61
𝑘𝑖 > 3 ; 𝐴𝑖 = 𝑥1 ∨ ⋯ ∨ 𝑥𝑝 ;
(𝑥1 ∨ 𝑥2∨ 𝑦1) ∧ (¬𝑦1 ∨ 𝑥3∨ 𝑦2) ∧ ¬𝑦2 ∨ 𝑥4∨ 𝑦3 … ∧
(¬𝑦𝑝−4 ∨ 𝑥𝑝−2∨ 𝑦𝑝−3) ∧ ¬𝑦𝑝−3 ∨ 𝑥𝑝−1∨ 𝑥𝑝 ;
1
2
On a i-3 nouvelles variables  on a i-2 clauses
exactement 3 littéraux.
Prouvons que est satisfiable ssi est satisfiable.
1 2
Prouver que f est polynomiale et
𝑓 𝑥 ∈ 3𝑆𝐴𝑇 𝑠𝑠𝑖 𝑥 ∈ 𝑆𝐴𝑇

62. Exercice 4 : Correction
62
Algorithme de f:
Pour i de 1 à n faire
selon (𝑘𝑖):
3: 𝐴′𝑖 = 𝐴𝑖
2: 𝐴′𝑖 = (𝑥1 ∨ 𝑥2∨ 𝑦1) ∧ (𝑥1 ∨ 𝑥2∨ ¬𝑦1);
1: 𝐴′𝑖= (𝑥1 ∨ 𝑦1∨ 𝑦2) ∧ (𝑥1 ∨ 𝑦1∨ ¬𝑦2) ∧ (𝑥1 ∨ ¬𝑦1∨ 𝑦2) ∧
(𝑥1 ∨ ¬𝑦1∨ ¬𝑦2);
sinon: 𝐴′𝑖= (𝑥1 ∨ 𝑥2∨ 𝑦1) ∧ (¬𝑦1 ∨ 𝑥3∨ 𝑦2) ∧
¬𝑦2 ∨ 𝑥4∨ 𝑦3 … ∧ (¬𝑦𝑝−4 ∨ 𝑥𝑝−2∨ 𝑦𝑝−3) ∧ (¬𝑦𝑝−3 ∨ 𝑥𝑝−1∨ 𝑥𝑝)
Fin selon
Fin pour  O(l) = O(max( 𝑘𝑖))
D’où f est calculable en un temps polynomiale

63. Exercice 4 : Correction
63
𝐴𝑖 = 𝑥1 ∨ 𝑥2∨ ⋯ ∨ 𝑥𝑝
 f(x)∈ 𝟑𝑺𝑨𝑻
x ∈ 𝑺𝑨𝑻
Existe-t-il une interprétation I /
[𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛
[𝑥1 ∨ 𝑥2∨ ⋯ ∨ 𝑥𝑝]𝐼= V 
∃ 𝑖 /[𝑥𝑖]𝐼=V
𝐼′
=
𝐼
[𝑦𝑗] =V 𝑝𝑜𝑢𝑟 𝑗 ≤ 𝑖 − 2
[𝑦𝑗] =F 𝑝𝑜𝑢𝑟 𝑗 > 𝑖 − 2
[𝐴′𝑖]𝐼′=V
 x ∈ 𝑺𝑨𝑻
Existe-t-il une interprétation I' /
[𝐴′𝑖]𝐼′=V ∀ 1 ≤ 𝑖 ≤ 𝑛′
On suppose que
[𝐴𝑖]𝐼=F ∀ 𝐼 𝑒𝑡 𝑥𝑗 𝐼
=F ∀ 𝑗;
 [𝑦𝑘]𝐼′=V ; 1 ≤ 𝑘 ≤ 𝑖 − 3
[¬𝑦𝑙−3 ∨ 𝑥𝑙−1∨ 𝑥𝑙]𝐼′= F
 [𝐴′𝑖]𝐼′=F ;  Contradiction
𝐷′
𝑜ù 𝑖𝑙 ∃ 𝐼/[𝐴𝑖]𝐼=V
f(x)∈ 𝟑𝑺𝑨𝑻

64. Exercice 5
a) Prouver que 𝐶𝑆 ∈ 𝑁𝑃𝐶, à
partir de 3SAT ∈ 𝑁𝑃𝐶.
b) Prouver que 𝐶𝑆 ∈ 𝑁𝑃.
64

65. Exercice 5 : Correction
65
b) Montrer que 𝐶𝑆 ∈ 𝑁𝑃:
• Soit S' est un sous ensemble de façon non
déterministe.
• Vérifier que |𝑆′
| ≤ 𝑘
Vérifier que ∀ 𝑠1, 𝑠2 ∈ 𝐴 𝑜𝑛 𝑎 𝑠1 ∈ 𝑆′𝑜𝑢 𝑠2 ∈ 𝑆′;
|𝑆′
| ≤ 𝑆 = 𝑛;
|𝐴| ≤ 𝑛2
 𝑶(𝒏𝟑
)
D’où C𝑺 ∈NP
 𝒏𝟐
𝒂𝒓ê𝒕𝒆𝒔 𝒑𝒐𝒖𝒓 𝒄𝒉𝒂𝒒𝒖𝒆 𝒂𝒓ê𝒕𝒆 𝒐𝒏 𝒂 𝟐𝒏  𝟐𝒏𝟑
 𝑶(𝒏)

66. Exercice 6
Prouver que 𝑇𝑆 ∈ 𝑁𝑃,
Clique ∈ 𝑁𝑃 et HC ∈ NP.
66

67. Correction Exercice 6: Prouver que 𝑇𝑆 ∈ 𝑁𝑃, HC ∈ N𝑃 et
Clique ∈ 𝑁𝑃.
• Soit une permutation 𝑣𝑝1, … , 𝑣𝑝𝑛 de façon non déterministe.
• Vérifier que 𝑖=1
𝑛−1
( 𝑣𝑝𝑖, 𝑣𝑝𝑖+1) + 𝑣𝑝𝑛, 𝑣𝑝1 ≤ 𝑏 (soit polynomial).
n distance à déterminer et pour chaque distance on parcours 𝑛2
éléments distincts.
Algorithme : 𝑛3
+ 𝑛 + 1 = 𝑂 𝑛3
 𝑻𝑺 ∈ 𝑵𝑷
HC ∝ 𝑇𝑆 𝑒𝑡 𝑇𝑆 ∈ NPC → CH ∈ NPC
67

68. Exercice 7
Étant donné 3-SAT est NPC
montrer que Clique ∈ 𝑁𝑃𝐶.
68

69. Correction Exercice 7 : Étant donné 3-SAT est
NPC montrer que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
1. Montrer que Clique ∈ 𝑁𝑃𝐶 : Donner un algorithme ND polynomial.
2. Montrer que Clique 𝑒𝑠𝑡 𝑁𝑃_𝐷𝑢𝑟 : Montrer que 3-SAT∝ 𝐶𝑙𝑖𝑞𝑢𝑒.
69
• Soit G=(S,A) et 𝑘 ≤ |𝑆|;
• ∃? 𝑆′ ⊆ 𝑆 𝑎𝑣𝑒𝑐 𝑆 ≥ 𝑘 𝑒𝑡 ∀ 𝑠1∈ 𝑆′𝑒𝑡 𝑠2 ∈ 𝑆′
𝑂𝑛 𝑎 𝑠1, 𝑠2 ∈ 𝐴.
Réponse

70. Correction Exercice 7 : Étant donné 3-SAT est
NPC montrer que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
70
• Choisir un sous − ensemble 𝑆′
⊆ 𝑆 𝑎𝑣𝑒𝑐 𝑆′
≤ 𝑘
F= True
Pour i de 1 à k-1 faire
Pour j de i+1 à k faire
Si (F=True) et 𝑠𝑖, 𝑠𝑗 ∈ 𝐴 alors …
Fin pour
Fin pour
Si (F=True) alors 𝑆′
est une clique
Algorithme
O(n2)=O(k2)
 f est calculable en un temps polynomiale et Clique ∈ 𝑵𝑷

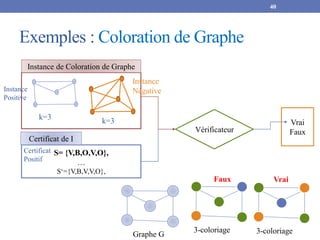
71. Correction Exercice 7 : Étant donné 3-SAT est
NPC montrer que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
71
Données :
Graphe 𝐺 = (𝑆, 𝐴), |𝑆|=n
et un entier 𝑘 ≤ |𝑆|
Problème :
Pour chaque clause 𝑐𝑖 on a 3
sommets |𝑆|=3m.
A sera construit comme suit : tous les
sommets sont reliés entre eux sauf les
2 sommets de même clause et si l’une
est la négation d’une autre.
𝑪𝒍𝒊𝒒𝒖𝒆
3 SAT
Données :
𝑃 = 𝑝1, 𝑝2, 𝑝3, … , 𝑝𝑛
A= 𝑐1 ∧ 𝑐2 ∧ ⋯ ∧ 𝑐𝑚
𝑐𝑖 = 𝑙𝑖1 ∨ 𝑙𝑖2 ∨ 𝑙𝑖3
Problème :
Existe-t-il une interprétation I
tel que
[𝐴𝑖]𝐼=V ∀ 1 ≤ 𝑖 ≤ 𝑛 ?

72. Correction Exercice 7 : Étant donné 3-SAT est
NPC montrer que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
72
• Transformer une expression booléenne 3-CNF en un graphe tel
que ce graphe contient une clique de taille k ssi l’expression
booléenne est satisfiable.
• Soit B = 𝑐1 ∧ 𝑐2 ∧ ... ∧ 𝑐𝑘 une formule en 3-CNF avec k clauses,
contenant chacune 3 littéraux distincts.
• Pour chaque clause on crée 3 sommets, un pour chaque littéral
dans la clause.
• On relie 2 sommets s’ils proviennent de deux clauses différentes
et que leurs littéraux sont consistent « l’un n’est pas la négation
de l’autre ».
Transformation

73. Correction Exercice 7 : Étant donné 3-SAT est
NPC montrer que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
73
Montrer que cette transformation est polynomiale:
• La construction de S se fait en O(m).
• La construction de A se fait en O(m2).
Exemple
B= 𝑐1 ∧ 𝑐2 ∧ 𝑐3
𝑐1 = 𝑎 ∨ ¬𝑏 ∨ ¬𝑐
𝑐2 = ¬𝑎 ∨ 𝑏 ∨ 𝑐
𝑐3 = 𝑎 ∨ 𝑏 ∨ 𝑐
k= m
𝑎1 𝑏1 𝑐1
𝑎3
𝑏3
𝑐3
𝑐2
𝑏2
𝑎2
𝒂, 𝒃, 𝒄 Vrai
¬𝒂, ¬𝒃, 𝒄 Vrai

74. Correction Exercice 7 : Étantdonné 3-SATest NPC montrerque
Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
74
” ”
Soit B une instance positive de 3-SAT, c.à.d. B est sous forme
CNF de 3 littéraux par clause et B est Satisfiable.
Montrer que G=f(B) est une instance positive de 𝐶𝑙𝑖𝑞𝑢𝑒.
c.à.d. il contient un sous-graphe complet de m sommets.
Si B est Satisfiable ∃ 𝐼 𝑡𝑒𝑙 𝑞𝑢𝑒[𝑐𝑗]𝐼=V ∀ 1 ≤ 𝑗 ≤ 𝑚
Alors 𝑖𝑙 ∃ 𝑎𝑢 𝑚𝑜𝑖𝑛𝑠 𝑢𝑛 𝑙𝑖𝑡𝑡é𝑟𝑎𝑙 𝑝𝑎𝑟 𝑐𝑙𝑎𝑢𝑠𝑒 𝑙𝑖 𝑡𝑒𝑙 𝑞𝑢𝑒 𝑙𝑖 𝐼=V
𝑆′ = 𝑙1, 𝑙2, 𝑙3, … , 𝑙𝑚  Montrer que 𝑆′
est une clique.
𝑆𝑜𝑖𝑡 𝑙𝑖, 𝑙𝑗 ∈ 𝑆′
𝑒𝑡 𝑙𝑖 ≠ ¬𝑙𝑗 et 𝑖 ≠ 𝑗 (puisqu’ils sont satisfiables
par I et ∉ à la même clause.
 (𝑙𝑖, 𝑙𝑗) ∈ 𝐴 d’où S' est une clique de taille ≥ 𝑘 = 𝑚.

75. Correction Exercice 7 : Étant donné 3-SATest NPC montrer
que Clique 𝑒𝑠𝑡 𝑁𝑃𝐶.
75
”  ”
Soit G une instance positive de f(B). G contient une clique S' de
taille k = m (nombre de clauses de B).  Montrer que B est
satisfiable et S' contient m sommets correspondant à m littéraux
pour chacune des clauses.
 ∃ une interprétation I qui en affectant à chacun de ces m
littéraux la valeur Vrai Car on n’a pas un littéral relié à sa
négation.
 D’où 3-SAT∝ 𝑪𝒍𝒊𝒒𝒖𝒆.
𝑶𝒏 𝒂 𝑪𝒍𝒊𝒒𝒖𝒆 𝒆𝒔𝒕 𝑵𝑷_𝑫𝒖𝒓 et 𝑪𝒍𝒊𝒒𝒖𝒆 ∈ 𝑵𝑷
D’où 𝑪𝒍𝒊𝒒𝒖𝒆 ∈ 𝑵𝑷_𝑪𝒐𝒎𝒑𝒍𝒆𝒕

76. Complexité en espace
76

77. Complexité en espace
77
Définition 1
Soit M une machine de Turing offline Déterministe.
La complexité en espace de la machine M est la fonction
EM (n) défini par :
EM (n) = max{ m, |x|=n, m est le nombre de cases visitées
lors de l’exécution de M sur x}

78. Complexité en espace
78
Définition 2
Soit M une machine de Turing offline Déterministe.
L’espace de calcule de la machine M sur un mot w est la
fonction EM (w) défini par :
EM (w) = {le nombre de cases visitées pour la plus
courte exécution de M sur w acceptant w}

79. Complexité en espace
79
Définition 3
Soit M une machine de Turing offline non Déterministe.
EM (n) = max{ECN (x) ; |x|=n}.
Définition 4
Une machine de Turing M est dite polynomiale en espace si :
∃ 𝑷 𝒏 /𝑬𝑴 (
𝒏) ≤ 𝑃 𝑛 ∀𝑛.

80. Complexité en espace
80
Définition 5
La classe P-space est la classe des langages décidés par
une MT Déterministe et polynomiale en espace.
Définition 6
La classe NP-space est la classe des langages acceptés par
une MT non Déterministe et polynomiale en espace.

81. Complexité en espace
81
Théorème
P-Space = NP-Space
et 𝑃 ⊆ 𝑁𝑃 ⊂ 𝑃_𝑠𝑝𝑎𝑐𝑒 est la classe des langages
décidés par une MT Déterministe et polynomiale
en espace.

82. Complexité en espace
82
Exercice : Prouver
L∈ 𝑁𝑃_𝑆𝑝𝑎𝑐𝑒
∃ 𝑴𝑻𝑵𝑫 𝑴 polynomiale en espace et
∃ 𝑷 𝒏 /𝑬𝑴(𝒏) ≤ 𝑃 𝑛 ∀𝑛.

83. Exercice : Prouver L∈ 𝑁𝑃_𝑆𝑝𝑎𝑐𝑒
∃𝑴𝑻𝑵𝑫 𝑴 polynomialeenespaceet ∃ 𝑷 𝒏 /𝑬𝑴(𝒏) ≤ 𝑃 𝑛 ∀𝑛.
Soit M' MTD qui reconnait L / L(M') =L.
EM' (n) ≤ 3𝑝 𝑛 = 𝑝′(𝑛)  L∈ 𝑃_𝑠𝑝𝑎𝑐𝑒
Donc 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒 ⊂ 𝑃_𝑠𝑝𝑎𝑐𝑒 et 𝑃_𝑠𝑝𝑎𝑐𝑒 ⊂ 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒
 𝑃_𝑠𝑝𝑎𝑐𝑒 = 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒.
83
𝑁𝑃 ⊂ 𝑃_𝑠𝑝𝑎𝑐𝑒
𝑁𝑃 ⊂ 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒
Soit L∈ 𝑁𝑃
∃ 𝑴𝑻𝑵𝑫 polynomiale en temps
∃ 𝑴𝑻𝑵𝑫 𝑴 𝒆𝒕 𝑷 𝒏 /𝑻𝑴 (
𝒏) ≤ 𝑃 𝑛 ∀𝑛
et on a 𝑬𝑴 𝒏 ≤ 𝑻𝑴 𝒏 ≤ 𝑃 𝑛
Donc 𝐿 ∈ 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒 = 𝑃_𝑠𝑝𝑎𝑐𝑒
 NP ⊂ 𝑁𝑃_𝑠𝑝𝑎𝑐𝑒 = 𝑃_𝑠𝑝𝑎𝑐𝑒.

84. Chapitre 3 : Paradigmes de programmation
84
Approche Diviser pour Régner
Algorithme de Gloutonne
Méthode Branch and Bound
Méthode Programmation Dynamique