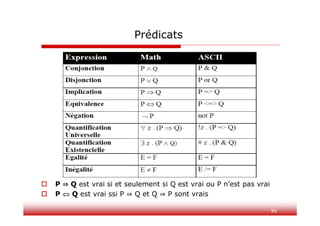
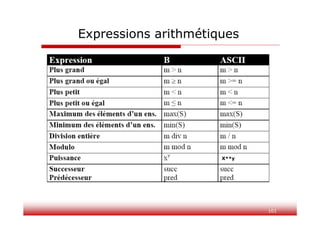
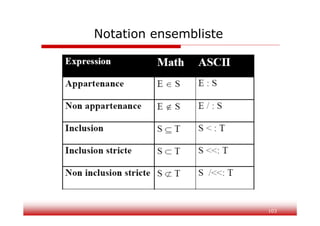
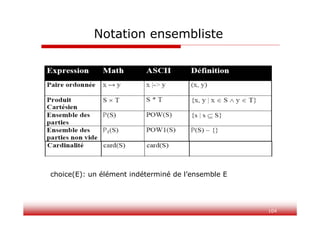
Le document présente la méthode B, une approche formelle pour le développement de logiciels, fondée sur la théorie des ensembles et la logique de premier ordre. Il décrit les concepts clés tels que la machine abstraite, les obligations de preuve et le raffinement, ainsi que l'utilisation de l'outil Atelier B pour faciliter la mise en œuvre de cette méthode. Des exercices pratiques illustrent la spécification et l'implémentation d'un système de réservation, démontrant la modularité et la vérifiabilité du processus.



![4
Historique
Née dans les années 80
Fondateur: Jean-Raymond Abrial (un
informaticien français )
Livre de référence: « The B Book » [1]
Le choix du nom B est une sorte
d'hommage aux membres du groupe
BOURBAKI.
C’est un groupe de mathématiciens français qui
a entrepris en 1939 une refonte des
mathématiques en les prenant à leur point de
départ logique.](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-4-320.jpg)




















































![Les obligations de preuve
Soient S une substitution et P un prédicat:
La notation [S] P se lit « la substitution S établit le
prédicat P »
[S] P représente le prédicat obtenu après
transformation de P par la substitution S.
Chaque substitution généralisée se définit en
précisant quel est le prédicat obtenu après
application de la substitution à un prédicat
quelconque.
Exemple pour la substitution simple:
[x:=E]I représente I dans laquelle toutes les
occurrences libres de x sont remplacées par E.
58](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-58-320.jpg)
![Les obligations de preuve
Le prédicat P c’est l’invariant I et la
substitution S est V, on obtient les
obligations de preuve suivantes:
Obligation de preuve de l’initialisation:
démontrer que le prédicat H [Init]I
est valide
Obligation de preuve pour une opération:
démontrer que le prédicat H [V]I est
valide
59](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-59-320.jpg)
![60
MACHINE
M
VARIABLES
V
INVARIANT
I
INITIALISATION
Init
OPERATIONS
u O(W) =
PRE
Q
THEN
V
END
END
Les obligations de preuve
Obligation de preuve pour l’initialisation:
Aucun hypothèse
But à prouver: I après Init (est ce que
l’initialisation établit l’invariant?) [Init]I
Obligation de preuve pour l’opération O:
On prouve que
lorsque la machine est dans un état
correct: les propriétés invariantes I
sont supposées vérifiées
lorsque l’opération est appelée avec la
pré-condition Q: Q est supposée
vérifiée
alors sa transformation V amène la
machine dans un état correct:
un état qui satisfait l’invariant I
I Q I après V
Exemple
I Q [V] I](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-60-320.jpg)
![61
MACHINE
M
VARIABLES
V
INVARIANT
I
INITIALISATION
Init
OPERATIONS
u O(W) =
PRE
Q
THEN
V
END
END
Les obligations de preuve
Les obligations de preuve pour la
machine M:
[Init]I
I Q [V] I
Exemple1](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-61-320.jpg)
![Les obligations de preuve
Exemple2
MACHINE
M(u)
CONSTRAINTS
C
CONSTANTS
c
PROPERTIES
R
VARIABLES
x
INVARIANT
I
INITIALISATION
U
OPERATIONS
r op(p) = PRE P THEN K END;
Obligation de preuve pour
l’initialisation:
C R [U]I
Obligation de preuve pour
l’opération O: C R I P [K] I](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-62-320.jpg)






![69
Substitution devient égal
Soit x une variable, e une expression et P
un prédicat, alors :
[ x := e ] P est le prédicat obtenu en
remplaçant toutes les occurrences libres
de x dans P par e.
Règle de typage:
Dans la substitution x := e, x et e doivent
être du même type T.
Dans la substitution x1,.., xn := e1, ..., en,
chaque xi doit être du même type que ei.](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-69-320.jpg)

![71
Exemple de calcul: OP de reserver
MACHINE
reservation
VARIABLES
nbPlacesLibres
INVARIANT
nbPlacesLibres 0..100
…
OPERATIONS
reserver(nbPlaces)=
PRE
nbPlaces NAT1
nbPlaces ≤ nbPlacesLibres
THEN
nbPlacesLibres :=
nbPlacesLibres-nbPlaces
END
END ```
I Q [V]I devient:
1. (nbPlacesLibres 0..100
nbPlaces NAT1 nbPlaces ≤nbPlacesLibres)
[nbPlacesLibres := nbPlacesLibres-nbPlaces]
(nbPlacesLibres 0..100)
2. (nbPlacesLibres 0..100
nbPlaces NAT1 nbPlaces ≤nbPlacesLibres)
(nbPlacesLibres-nbPlaces 0..100)](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-71-320.jpg)
![72
Substitution simultanée
Correspond à l’exécution simultanée
de deux substitutions
Deux syntaxes:
x := E | | y := F
x, y := E, F
Sémantique
[x, y := E, F] I
[z := F][x := E][y := z]I z étant une variable distincte
de x et y et non libre dans I](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-72-320.jpg)
![73
Substitution simultanée
Exemple: permutation de 2 variables
[x, y := y, x] (x < y)
[z := x][x := y][y := z] (x < y)
[z := x][x := y] (x < z)
[z := x] (y < z)
(y < x)](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-73-320.jpg)
![74
Substitution choix borné
Permet de définir un nombre fini de
comportements possibles sans préciser
lequel sera effectivement choisi (non
déterministe).
n'est pas une substitution d'implémentation
Syntaxe
CHOICE S1 OR ... OR Sn END
S1, ..., Sn des substitutions (avec n ≥ 2)
Sémantique
[CHOICE S1 OR ... OR Sn END] I [S1] I ... [Sn] I](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-74-320.jpg)
![75
Substitution choix borné
Exemple : Définition des résultats de l’examen du permis de
conduire
CHOICE résultat := réussite ||
permis := permis U {candidat}
OR résultat := échec
END
Calculer :
[CHOICE résultat := réussite || permis := permis U {candidat}
OR résultat := échec END] (permis PERS-MAJEUR)](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-75-320.jpg)
![76
Select (Garde et Choix Borné)
La substitution SELECT permet d’exprimer des
gardes qui définissent les conditions
d’exécution de l’instruction.
Syntaxe Sémantique
[SELECT Q1 THEN S1 (Q1 ⇒ [S1]I)
WHEN Q2 THEN S2 (Q2 ⇒ [S2]I)
… …
WHEN Qn THEN Sn (Qn ⇒ [Sn]I)
[ELSE SE] ((Q1Q2…Qn)⇒ [SE]I)
END]
Les gardes peuvent ne pas être disjointes, dans
ce cas le comportement est non-déterministe.](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-76-320.jpg)

![78
Substitution identité
La substitution identité Skip ne
modifie pas le prédicat sur lequel elle
est appliquée.
Elle est notamment utilisée pour
décrire que certaines branches d’une
substitution IF, CASE ou SELECT ne
modifient pas les variables.
Sémantique:
[skip] I I](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-78-320.jpg)
![79
La substitution CASE permet de définir différents
comportements possibles en fonction de la valeur d’une
expression.
Syntaxe:
CASE E OF
EITHER L1 THEN S1
[OR L2 THEN S2
…
OR Ln THEN Sn]
[ELSE SE]
END
Chaque branche EITHER et OR est constituée d’une liste
non vide de constantes littérales (entier, énuméré,
booléen).
Les L1, .. , Ln doivent être disjoints (déterminisme) et de
même type que E.
Si le ELSE est absent, l’échec des Li réalise la substitution
skip.
Condition par Cas](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-79-320.jpg)
![80
Condition par Cas
Sémantique:
CASE E OF
EITHER L1 THEN S1 E{L1} [S1]I
[OR L2 THEN S2 E{L2} [S2]I
… …
OR Ln THEN Sn] E{Ln} [Sn]I
[ELSE SE] E{L1,L2…Ln} [SE]I
(en l’absence de ELSE
END SKIP)](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-80-320.jpg)

![82
Substitution conditionnelle IF
La substitution conditionnelle IF est définie
selon plusieurs formes :
1. IF P THEN S END
Sémantique
[P S]I P [S]I
2. IF P1 THEN S1 ELSE T END
Sémantique
[IF P1 THEN S1 ELSE T END]I
(P1 [S1]I) (¬P1 [T]I)](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-82-320.jpg)
![83
3. Forme générale du IF
Syntaxe: Sémantique:
IF P1 THEN S1 P1 ⇒ [S1]I
[ELSIF P2 THEN S2 P1P2 ⇒ [S2]I
… …
ELSIF Pn THEN Sn] P1P2…Pn-1Pn ⇒ [Sn]I
[ELSE SE] P1P2…Pn-1Pn ⇒ [SE]I
END
Substitution conditionnelle IF](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-83-320.jpg)


![86
Exemple de calcul de l’opération
changerT
MACHINE Chaudiere
SETS
ETATS = {activé, désactivé}
VARIABLES
T, Alarme
INVARIANT
T NAT
Alarme ETATS
(T > 130) (Alarme = activé)
….
OPERATIONS
changerT (v) ==
PRE
v NAT v ≤ 130
THEN
T := v
END
…
I Q [V]I devient
1. T NAT Alarme ETATS
((T > 130) (Alarme = activé))
v NAT v 130
[T := v] (T NAT Alarme ETATS
((T > 130) (Alarme = activé)))
Après application de la substitution, on obtient:
2. T NAT Alarme ETATS
((T > 130) (Alarme = activé))
v NAT v 130
(v NAT
Alarme ETATS
((v > 130) (Alarme = activé))).](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-86-320.jpg)
![87
Exemple de calcul: opération changerT
I Q [V]I devient
1. T NAT Alarme ETATS
((T > 130) (Alarme = activé))
v NAT alarme = désactivé
(v ≤ 130 [T := v]
(T NAT
Alarme ETATS
((T > 130) ) (Alarme = activé)))
(v > 130
[T := v || alarme := activé]
(T NAT
Alarme ETATS
((T > 130) ) (Alarme = activé)))
…
MACHINE Chaudiere
SETS
ETATS = {activé, désactivé}
VARIABLES
T, Alarme
INVARIANT
T NAT
Alarme ETATS
(T > 130) ) (Alarme = activé)
INITIALISATION …
OPERATIONS
changerT (v) ==
PRE
v NAT alarme = désactivé
THEN
IF (v ≤ 130) THEN T := v
ELSE T:= V || alarme := activé
END
…](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-87-320.jpg)
![88
Substitution Choix non borné
Syntaxe:
ANY x WHERE Q THEN S END
L’instruction ANY correspond à un choix arbitraire
d’une valeur de x suivant le prédicat Q
La variable x doit être typée dans Q
Non déterministe et n’est pas une substitution
d’implémentation
Sémantique
x.(Q ⇒ [S]I)
Avec plusieurs variables (qui doivent être deux à deux
distinctes):
ANY x1,x2,…,xn WHERE Q THEN T END](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-88-320.jpg)

![90
Dérivées du choix non borné
Substitution « devient élément de »
Syntaxe: X:E
Avec E un ensemble, X une liste de variables modifiables non vide.
Sémantique:
X : E ANY Y WHERE Y E THEN X := Y END
Y.(Y E [X:=Y]I)
Exemples :
i1 : INT ;
b1 : BOOL ;
x1 : -10 .. 10 ;
y1, y2 : {1, 3, 5} * NAT](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-90-320.jpg)
![91
Dérivées du choix non borné
Substitution « devient tel que »
Syntaxe: x:(Q)
Avec Q un prédicat, X une liste de variables modifiables
deux à deux distinctes.
Les variables de la liste X, doivent être typées dans le
prédicat Q
Sémantique:
X :(Q) ANY Y WHERE [X:=Y]Q THEN X:=Y END
Exemples :
x : (x INT x > -4 x < 4) ;
a, b : (a INT b INT a2 + b2 = 25) ;](https://image.slidesharecdn.com/chapitre2partie1-230305144938-5cdb084a/85/Chapitre2_Partie1-pdf-91-320.jpg)