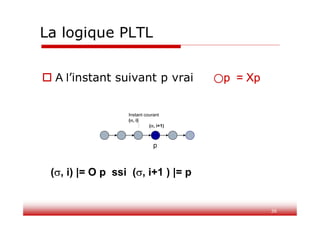
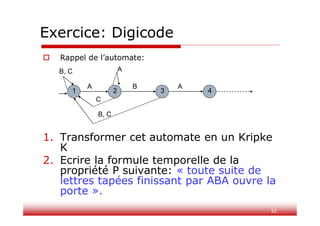
Ce document traite du model checking, une méthode automatique pour vérifier si un automate satisfait une formule temporelle. Il présente la structure de Kripke comme modèle formel et explore les logiques temporelles, notamment PLTL et CTL, utilisées pour spécifier des propriétés dynamiques des systèmes. Des exemples pratiques et des représentations d'automates sont fournis pour illustrer les concepts abordés.

1. 1
Cours "Génie Logiciel II"
Chapitre3: Vérification de
modèles (Model checking)
Niveau: II2
Enseignante: Rim DRIRA
rim.drira@ensi-uma.tn

2. 2
Plan
1. Introduction
2. Définition
3. Structure Kripke
4. Logique temporelle
1. PLTL
2. CTL
5. Algorithme de model checking de CTL

3. 3
Préliminaire: Application des logiques
pour la vérification
 Logique propositionnelle
 Logique des prédicats du 1er ordre
 Logique des prédicats d’ordre supérieur
 Logique temporelle /Logique modale
 Etc.
 Chaque logique comporte un langage
formel pour:
 Modéliser de manière formelle des objets
 Raisonner sur les propriétés de ces objets

4. 4
Préliminaire: Application des logiques
pour la vérification
1. Théorie des preuves (sur laquelle
se base la méthode B)
2. Théorie de modèles (ce que nous
allons étudier dans ce chapitre)

5. Théorie des preuves
 Un système formé d’une logique comporte:
 une notation (syntaxe)
 un ensemble d’axiomes (faits)
 un ensemble de règles d’inférence
(déduction)
 Une preuve formelle est une séquence de
situations où chaque situation est déduite à
partir d’autres situations par l’application
de règles d’inférence.
5
Préliminaire: Application des logiques
pour la vérification

6. 6
Théorie de modèles
 La seconde utilisation de la logique
est pour exprimer des situations au
moment de l’exécution
 Le langage de la logique est utilisé ici
pour formaliser des propriétés de
structures et de déterminer quand
une situation est vraie dans cette
structure
Préliminaire: Application des logiques
pour la vérification

7. 7
Théorie de modèles
 Spécification des propriétés est
représentée par des formules (
logique temporelle)
 Implémentation représentée par des
formules ou par un modèle
sémantique automate (système de
transitions)
Préliminaire: Application des logiques
pour la vérification

8. 8
Model checking

9. 9
Définition
 Méthode exhaustive et automatique
qui permet de savoir si un automate
donné vérifie une formule
temporelle donnée
 Les systèmes qui se prêtent le mieux
aux techniques de model checking
sont ceux facilement modélisables par
automate (fini).

10. 10
Model checking
 Pour appliquer la méthode du model-
checking, il faudra:
1. Construire une modélisation formelle du
système
 Utiliser un langage de spécification formelle
(Exemple: une structure Kripke)
2. Énoncer formellement les propriétés à
vérifier
 Utiliser un langage de spécification de
propriétés (une logique temporelle)
3. Appliquer un algorithme de vérification
incarné dans un model checker

11. 11
Model checking
M = Modèle (Système de transitons)
 = Formule temporelle
Model checking : est ce que M |= 

12. 12
Model checking
Exemple

13. Exemples de modélisation
 https://www.univ-
orleans.fr/lifo/membres/Yohan.Boichu
t/Enseignement/Verif/Cours-Verif.pdf
13

14. 14
Modélisation formelle:
Structure Kripke

15. 15
 Une structure Kripke est un
automate où
 les états sont étiquetés par les
propositions atomiques qu’ils vérifient.
 Les étiquettes des transitions ont moins
d’importance.
Définition

16. 16
Structure Kripke
 La Structure Kripke est un automate
A, quintuple de la forme :
A = { Q, E, T, q0, l}
 Q : ensemble d’états,
 E : ensemble d ’étiquettes de transitions,
 T Q x E x Q : ensemble de transitions,
 q0 : état initial
 l : application qui associe à chaque état
de Q des propriétés élémentaires
vérifiées dans cet état.

17. 17
Structure Kripke
 Exemple: Digicode pour l’ouverture
de portes de bureaux ou
d’immeubles:
 la porte s'ouvre dès qu'on tape la bonne
suite de caractères: ABA
 Pour simplifier, 3 touches possibles: A, B,
C
 Il est possible de se tromper, on ouvre la
porte dès que la fin de la séquence de
touches est ABA.

18. 18
Structure Kripke
A B A
1 2 3 4
C
B, C
A
B, C
Q = {1, 2, 3, 4} T= {(1,A,2), (1,B,1), (1,C,1), (2,A,2),
E = {A, B, C} (2,B,3), (2,C,1), (3,A,4), (3,B,1),
q0 = 1 (3,C,1)}
Exemple : Le digicode: L’automate

19. 19
A
A B A
1 2 pA
3 pB
pred2
4 pA
pred3
C
B, C
B, C
Q = {1, 2, 3, 4}
q0 = 1
T= {(1,A,2), (1,B,1), (1,C,1), (2,A,2),
(2,B,3), (2,C,1), (3,A,4), (3,B,1),
(3,C,1)}
E = {A, B, C}
l = {1 ↦ Φ, 2 ↦ {pA}, 3 ↦ {pB, pred2},
4 ↦ {pA, pred3}}
Structure Kripke
Exemple : Le digicode: La structure Kripke
pA: On vient de taper un A
pB: On vient de taper un B
pC: On vient de taper un C
Pred2: l’état précédent un 2
Pred3: l ’état précédent est un 3

20. 20
Arbre d’exécution
 Il est souvent nécessaire, par exemple
pour appliquer des méthodes de
model-checking, de raisonner sur un
arbre d’exécution d’une structure
Kripke :
 C’est un arbre infinie représentant tous les
chemins de la structure.
 sa racine est l’´etat initial de la structure,
 Le(s) successeurs de chaque nœud sont
ses successeurs par la relation de
transition.

21. 21
Arbre d’exécution
1
1 2
2
1 1 2
2 1
3
1 1 1
2 2
3
2
1 3 4
C ’est le début de l ’arbre
 Exemple1:Arbre d’exécution du digicode

22. 22
Structure Kripke
 Exemple2:

23. 23
Structure Kripke-Quelques variables en plus
 Rappel de l’automate du Digicode: Il est possible de se
tromper, on ouvre la porte dès que la fin de la séquence de
touches est ABA.
 Modifier l’automate afin de:
 Permettre de tolérer au maximum trois erreurs,
 Ajouter des transitions déclenchant une alarme lorsque
quatre erreurs sont commises.
A B A
1 2 3 4
C
B, C
A
B, C

24. 24
A B A
1 2 3 4
Si ctr = 3
A, C
ctr := ctr +1
err
Si ctr < 3
C
ctr := ctr +1
Si ctr = 3
B, C
ctr := ctr +1
Si ctr = 3
B, C
ctr := ctr +1
Si ctr < 3
B, C
ctr := ctr +1
Si ctr < 3
A
ctr := ctr +1
Si ctr< 3
B, C
ctr := ctr +1
Réponse: Quelques variables en plus

25. 25
Remarques: Quelques variables en plus
 Lorsqu’on modélise des systèmes réels, il est souvent
commode de permettre aux automates de manipuler des
variables d’états.
 Les liens entre un automate et les variables peuvent être
de deux types:
 Affectations : Une transition peut modifier la valeur
d’une ou de plusieurs variables.
 Exemple: toutes les transitions sauf (1, A, 2), (2, B, 3) et
(3, A, 4) incrémentent le compteur.
 Gardes : Une transition peut être gardée par une
condition sur les variables. Ainsi, le franchissement de la
transition n’est possible que si la condition est vérifiée.
 Exemple: les transitions correspondant à une erreur (1, B,
1), (1, C, 1), (2, C, 1), etc. sont gardées par la condition
ctr < 3.

26. 26
Les logiques temporelles
Suggérées pour la première fois par Pnueli en 1977

27. 27
Motivations
Exemples
 P1: toute demande d’un ascenseur doit être satisfaite.
 Pour formaliser cette propriété, nous avons besoin
d’indiquer « la position au temps t ». En utilisant la
logique des prédicats du premier ordre :
 App(n,t): l’existence d’un appel pour l’étage n au temps t
 Dess(n,t): la desserte de l’étage n au temps t
 Une propriété un peu plus compliquée:
 P2: Un ascenseur ne traverse jamais un étage pour
lequel un appel existe sans le satisfaire.
 H(t): la position de la cabine à l’instant t

28. 28
Motivations
 La logique du premier ordre permet d’écrire les
propriétés dynamiques en utilisant un temps explicite
MAIS les formules deviennent vite très lourdes.
La logique temporelle est mieux appropriée
 Le paramètre t disparaît
 Des constructions sont proposées pour exprimer le
futur ou le passé.
 On peut écrire P1 de l’exemple de l’ascenseur avec la
logique temporelle PLTL (futur):
⃞(appel → ⃟ desserte)

29. 29
Logiques temporelles
 Une formule de la logique temporelle est
formée à partir :
1. Des propositions atomique: Une proposition
atomique décrit une propriété vérifiée dans
un état.
2. Des combinateurs temporels:
inévitablement, toujours, etc.
3. Des combinateurs booléens classiques:
négation, ou, et, implication, équivalence.
Logique temporelle= Logique classique + opérateurs
dédiés au temps

30. 30
Les logiques temporelles
 Deux grandes classes
 Logique temporelle linéaire: ex: PLTL
 Logique temporelle arborescente: ex:
CTL

31. 31
La logique temporelle
linéaire
PLTL

32. 32
La logique PLTL
 PLTL: Propositional Linear Temporal
Logic
 Temps linéaire: chaque instant possède
un seul instant successeur
 Opérateurs temporels:
inévitablement, toujours, jusqu’à,
juste après.

33. 33
La logique PLTL
Temps Linéaire: PLTL permet d’exprimer
des propriétés temporelles relatives à des
exécutions linéaires

34. 34
La logique PLTL
 Inévitablement p ⃟ p = Fp
p
Instant
courant

35. 35
La logique PLTL
 Toujours p ⃞p = Gp
p p p p
Instant
courant

36. 36
La logique PLTL
 A l’instant suivant p vrai ⃝p = Xp
p
Instant courant
(, i)
(, i+1)
(, i) |= O p ssi (, i+1 ) |= p

37. 37
La logique PLTL
 p jusqu’à q p  q
p p p q
Instant
courant

38. Exercice
 Exprimer en PLTL:
1. A partir d’une alerte, nous serons dans un état
d’arrêt (plus tard).
2. A partir d’une alerte, l’alarme est en marche
jusqu’à l’arrêt qui suivra forcément.
3. Toute demande sera suivie d’une
réponse.
4. Pas d’accès simultané à une section
critique
38

39. 39
 Exprimer en PLTL:
 A partir d’une alerte, nous serons dans un état
d’arrêt (plus tard):
⃞ (alerte → ⃟ arrêt).
 A partir d’une alerte, l’alarme est en marche
jusqu’à l’arrêt qui suivra forcément:
⃞ (alerte → (alarme  arrêt))
Solution
alerte
Alarme U arret
arret
aame arm arm arm arm arm

40. 40
 Exprimer en PLTL
 Toute demande sera suivie d’une
réponse
(demande → réponse)
 Pas d’accès simultané à une section
critique
┐(acces_A  acces_B)
Solution

41. La logique PLTL
41
 Syntaxe
 Les propositions atomiques sont des
formules PLTL
 Si p et q sont deux formules alors
 p  q, ┐p, p  q et ⃝p
 Abréviations
 p∨q = ┐(┐p  ┐q)
 p q = ┐p ∨ q
 false = ┐true
 p q = p q  q p
 ⃟p = true  p true = p ∨ ┐p
 ⃞p = ┐⃟ ┐p

42. 42
La logique PLTL
 Dualité:  est le dual de 
 p =    p (s’il fera beau dorénavant, il est
faux que finalement il pleuvra!)
 p =   p (si finalement je serai riche, il
est faux que je serai toujours pauvre!)
 Et donc aussi (par élimination des
doubles négations)
  p =   p
   p =   p

43. 43
La logique PLTL
Combinaisons
 Infiniment souvent p:  p
 P est vérifié un nombre infini de fois le
long de l’exécution
 Finalement toujours p:  p

44. 44
Exercice
 Est-ce p  q et q  p sont équivalentes?
 La réponse est négative, car
  p   q =   p   q
 Ceci est vrai dans le cas où p est dorénavant faux ou
q se vérifie enfin
  q   p =   q   p
 Ceci est vrai dans le cas où q est dorénavant faux ou
p se vérifie enfin

45. 45
Satisfaction et sémantique des
opérateurs temporels

46. Automate logiques
temporelles
Rappel

47. 47
Notations
 A |=  : l’automate A satisfait  est défini par:
 A |=  ssi , 0 |=  pour toute exécution  de A
 : une formule temporelle à vérifier
 : une séquence d’états décrivant une exécution d’un
système. Exemple:  = (0, 0), (1, 1), … (n, n)….
 (i) est i-ème état de l’exécution 
 ||: longueur d’un chemin 
 A, , i |=  : au temps i de l’exécution ,  est vraie.
 A, , i |  :  n’est pas satisfaite au temps i de .
 Remarque: Dans les notations, A est très souvent implicite et on
l’omet dans les écritures (on écrit: , i |= ).
Concept de satisfaction, symbole╞

48. 48
, i |= p ssi p  l((i))
, i |=  ssi il n’est pas vrai que , i |= 
, i |=   ssi , i |=  et , i |= 
, i |= X ssi i < || et , i+1 |= 
, i |= F ssi il existe j tel que i  j  || et , j |= 
, i |= G ssi pour tout j tel que i  j  ||, on a , j |= 
, i |=    ssi il existe j, i  j  || tel que , j |=  et
pour tout k tel que i  k <j, on a , k |= ,
Sémantique de la logique PLTL
Rappel

49. 49
Sémantique de la logique PLTL
 La définition de , i |=  se fait par induction
sur la structure de :
 la valeur de vérité d’une formule composée est
donnée à partir des valeurs de vérité de ses sous-
formules.
 Exemple:
j 0 1 2 3 4 5 6
X 0 0 1 1 0 0 1
X = 0 T T F F T T F
X = 1 F F T T F F T
O(x=1) F T T F F T
(x=0)  O(x=1) F T F F F T F

50. 50
Sémantique de la logique PLTL
j 0 1 2 3 4 5 6
X 0 0 1 1 0 0 1
X = 0 T T F F T T F
X = 1 F F T T F F T
O(x=1) F T T F F T
(x=0)  O(x=1) F T F F F T F
((x=0)  O(x=1)) F F F F F F F
((x=0) 
O(x=1))
T T T T T T F
(, i) |=O F ssi (, i+1 ) |= F
(, i) |= F ssi  j i (, j ) |= F

51. 51
Sémantique de la logique PLTL
 Exemples
j 0 1 2 3 4 5 6
X 1 3 2 4 3 5 4 …
X > 3 F F F T F T T …
 (X > 3) F F F F F T T …
j 0 1 2 3 4 5
X 1 2 3 4 5 6 …
X = 4 F F F T F F …
 (X = 4) T T T T F F …

52. 52
Exercice: Digicode
 Rappel de l’automate:
1. Transformer cet automate en un Kripke
K
2. Ecrire la formule temporelle de la
propriété P suivante: « toute suite de
lettres tapées finissant par ABA ouvre la
porte ».
A B A
1 2 3 4
C
B, C
A
B, C

53. 53
A
A B
A
1 2 pA 3 pB
4 pA
PO
C
B, C
B, C
Réponse: Digicode
PA: On vient nécessairement de taper A
PB: On vient nécessairement de taper B
PO: Porte ouverte
Propriété P (vivacité): G(X PA  XX PB  XXX PA XXX PO)

54. 54
Arbre d’exécutiondu digicode
1
1 2
2
1 1 2
2 1
3
1 1 1
2 2
3
2
1 3 4
C ’est le début de l ’arbre
Propriété P (vivacité): G(X PA  XX PB  XXX PA XXX PO)
pA
pA pA pB
pB
pB
pO
pA
PA: On vient nécessairement de taper A
PB: On vient nécessairement de taper B
PO: Porte ouverte

55. 55
Limites de l’expressivité de PLTL
 Formules de chemins: les connecteurs
temporels considèrent une exécution à la
fois
 Impossible de pouvoir savoir si tout
ou partie des exécutions partant d’un
état donné vérifient une propriété