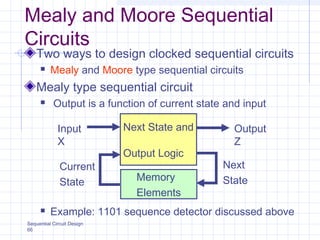
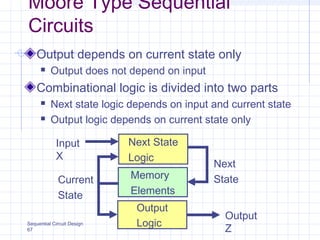
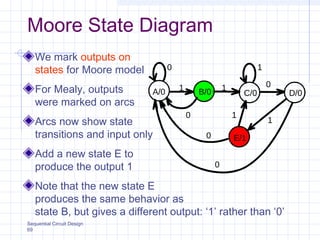
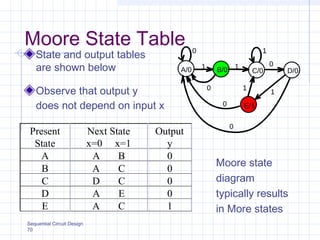
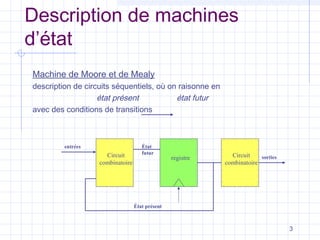
Ce document présente les modèles de machines d'état de type Moore et Mealy, mettant en avant les différences entre ces deux modèles concernant la dépendance des sorties par rapport aux états et aux entrées. Il explique également la conception des circuits séquentiels à l'aide de diagrammes d'état, de tables de transition, et fournit des exemples pratiques, notamment sur le fonctionnement d'un essuie-glace. Des aspects de codage et des méthodes de simplification pour la synthèse des machines d'état sont également abordés.


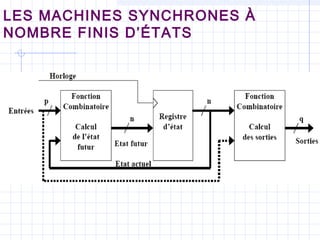
![Conception des Machines
d'état
Circuit d'excitation
Calcul combinatoire
des états FUTURS
du système : G
c
D Q
Circuit
de sortie
F
Entrées
Horloge
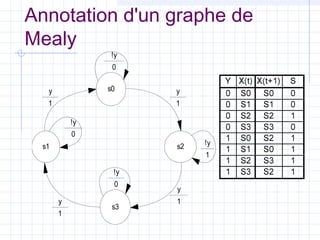
X(t)X(t+1) S(t)
E(t)
S(t) = F(X(t))
X(t + 1) = G[E(t), X(t)]
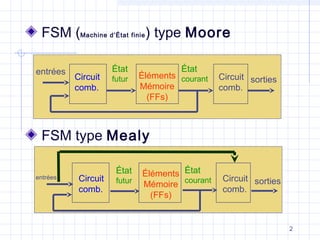
Machine de Moore](https://image.slidesharecdn.com/coursmooremealyautosaved-170802082038/85/Cours-mooremealy-autosaved-7-320.jpg)
![Conception des Machines
d'état
Machine de Mealy
Circuit d'excitation
Calcul combinatoire
des états FUTURS
du système : G
c
D Q
Circuit
de sortie
F
Entrées
Horloge
X(t)X(t+1)
S(t)
E(t)
S(t) = F[X(t), E(t)]
X(t + 1) = G[E(t), X(t)]](https://image.slidesharecdn.com/coursmooremealyautosaved-170802082038/85/Cours-mooremealy-autosaved-8-320.jpg)