Ce document aborde le problème du plus court chemin (PCC) dans la théorie des graphes, en présentant des définitions, des conditions d'optimalité et divers algorithmes de résolution tels que Dijkstra, Bellman, Ford et Floyd. Chaque algorithme est expliqué avec des exemples pour illustrer leur utilisation dans la détermination du chemin le plus court entre des sommets dans des graphes orientés et non orientés, avec ou sans circuits. Des applications pratiques du PCC dans des domaines comme les réseaux routiers et les télécommunications sont également discutées.

1. CHAPITRE II:
PROBLÈME DU PLUS COURT
CHEMIN
Université Blida 1
Faculté des Sciences
Département d’Informatique
Master IL (Ingénierie Logiciel) & SIR (Systèmes
Informatiques et Réseaux)
Semestre 1
Mme AROUSSI (s_aroussi@esi.dz)
2018-2019
Disponible sur https://sites.google.com/a/esi.dz/informatiqueblida/

2. Introduction
Définition
Conditions (Optimalité/ Nécessaire)
Algorithmes de Résolution
Algorithme de DIJKSTRA
Algorithme de BELLMAN
Algorithme de FORD
Algorithme de FLOYD
2
PLAN DU CHAPITRE II

3. 3
Le problème du Plus Court Chemin (PCC)
compte parmi les problèmes le plus classiques
de la théorie des graphes et les plus importants
dans leurs applications (les problèmes
d'optimisation de réseaux routiers ou
télécommunications, les problèmes de tournées,
….)
INTRODUCTION

4. 4
Ce problème du Plus Court Chemin (PCC) peut être posé
de la façon suivante:
Etant donné un graphe orienté valué G (X,U,L), on
associe à chaque arc u(i,j) un nombre réel l(u) ou lij,
appelé la longueur ou le poids de l’arc, le PCC entre
deux sommets s (source ou origine) et d (destination)
du graphe consiste à déterminer, parmi tous les
chemins allant de s à d, un chemin, noté u*, dont la
longueur totale l(u*) = soit minimale
DÉFINITION

5. 5
Condition Nécessaire: Le problème du plus court
chemin a une solution si et seulement s’il n'existe pas
dans le graphe de circuit de longueur strictement
négative pouvant être atteint à partir de l’origine (s).
Un circuit négatif est appelé circuit absorbant
INTRODUCTION
aaaa
ffff
bbbb
eeee
-3
-3
-1
cccc
dddd
5
-510
2

6. 6
Condition d’Optimalité: Les sous-chemins des plus
courts chemins sont des plus courts chemins.
INTRODUCTION
Exemples des arborescences des
plus courts chemins dont l’origine
est a
aaaa
bbbb
eeee
cccc
dddd
3
5
3
1 2
6
6
4
72
aaaa
bbbb
eeee
cccc
dddd
3
5
6
6
aaaa
bbbb
eeee
cccc
dddd
3
2
4
2

7. 7
Selon les propriétés du graphe traité (orienté/non
orienté, avec/sans circuit ou longueurs
positives/quelconques) et selon le problème considéré
(recherche du plus court chemin d'un sommet vers
tous les autres, ou entre tous les couples de
sommets), il existe de nombreux algorithmes
permettant l'obtention d'une solution.
ALGORITHMES DE RÉSOLUTION

8. 8
ALGORITHMES DE RÉSOLUTION
Algorithmes Type du
PCC
Propriétés du graphe
Type de graphe Longueur
Dijkstra D’un
sommet à
tous les
autres
sommets
Graphe orienté (et non
orienté)
Positive
Bellman Graphe orienté sans
circuit (sommet
d’origine doit être sans
prédécesseur)
Quelconque :
Positive et/ou
Négative
Ford Graphe orienté
Floyd Entre tous
les
couples de
sommets
Graphe orienté

9. 9
Cet algorithme permet de calculer le PCC d’un sommet «
s » à un sommet « d » ou d’un sommet « s » à tous les
autres sommets dans un graphe de longueur positive.
Soit π(i) la valeur de chemin du sommet « s » vers le
sommet « i », ainsi, initialement : π(s) = 0 et π(x) = ∞
pour tout sommet x ≠s
Soit M l’ensemble des sommets marqués, initialement
il est vide (M = φ )
ALGORITHME DE DIJKSTRA

10. 10
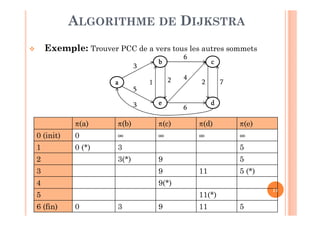
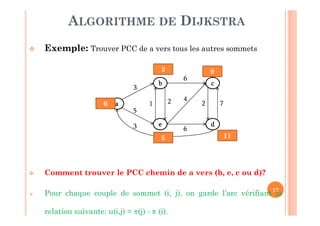
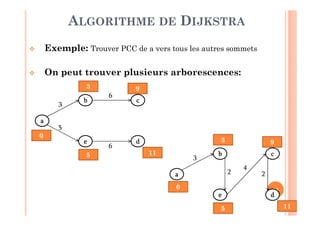
Tant qu’il existe un sommet non marqué (M≠X) ou on
n’a pas arrivé au sommet destinataire (x ≠ d) faire:
1. Choisir un sommet non marqué, soit x (x∈X-M),
ayant le plus petit π [π(x) = min {π(y) tq y∈X-M}]
2. Mettre à jour ses successeurs non encore marqués
comme suit: π(y) = min (π(y), π(x)+lxy) tel que y∈ Γ+ (x) ∩ (X-
M)
3. Marquer le sommet x [M = M ∪ {x}]
ALGORITHME DE DIJKSTRA

11. 11
Exemple: Trouver PCC de a vers tous les autres sommets
ALGORITHME DE DIJKSTRA
π(a) π(b) π(c) π(d) π(e)
0 (init) 0 ∞ ∞ ∞ ∞
1 0 (*) 3 5
2 3(*) 9 5
3 9 11 5 (*)
4 9(*)
5 11(*)
6 (fin) 0 3 9 11 5
aaaa
bbbb
eeee
cccc
dddd
3
5
3
1 2
6
6
4
72

12. 12
Exemple: Trouver PCC de a vers tous les autres sommets
Comment trouver le PCC chemin de a vers (b, e, c ou d)?
Pour chaque couple de sommet (i, j), on garde l’arc vérifiant la
relation suivante: u(i,j) = π(j) - π (i).
ALGORITHME DE DIJKSTRA
aaaa
bbbb
eeee
cccc
dddd
3
5
3
1 2
6
6
4
72
9
0
5
3
11

13. 13
Exemple: Trouver PCC de a vers tous les autres sommets
On peut trouver plusieurs arborescences:
ALGORITHME DE DIJKSTRA
aaaa
bbbb
eeee
cccc
dddd
3
5
6
6
9
0
5
3
11
aaaa
bbbb
eeee
cccc
dddd
3
2
4
2
9
0
5
3
11

14. 14
Cet algorithme permet de calculer le PCC d’un sommet «
s » à un sommet « d » ou d’un sommet « s » à tous les
autres sommets dans un graphe orienté sans circuit de
longueur quelconque.
Soit π(i) la valeur de chemin du sommet sans prédécesseur
« s » vers le sommet « i », ainsi, initialement : π(s) = 0 et π(x) =
∞ pour tout sommet x ≠s
Soit M l’ensemble des sommets marqués, initialement il
contient « s » (M = {s} )
Soit Z l’ensemble des sommets ayant au moins un
prédécesseur. Il contient aussi « s » Z = Z ∪ {s}
ALGORITHME DE BELLMAN

15. 15
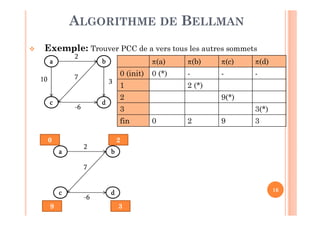
Tant qu’il existe un sommet non marqué (M≠Z) ou on
n’a pas arrivé au sommet destinataire (x ≠ d) faire:
1. Choisir un sommet non marqué, soit x (x∈Z-M), dont
tous les prédécesseurs sont marqués [Γ-(x) ⊂ M]
2. Mettre à jour son poids π comme suit: π(x) = min
(π(y)+lyx) tel que y∈ Γ-(x)
3. Marquer le sommet x [M = M ∪ {x}]
ALGORITHME DE BELLMAN

16. 16
Exemple: Trouver PCC de a vers tous les autres sommets
ALGORITHME DE BELLMAN
π(a) π(b) π(c) π(d)
0 (init) 0 (*) - - -
1 2 (*)
2 9(*)
3 3(*)
fin 0 2 9 3
aaaa
cccc
bbbb
dddd
10
2
-6
7
3
aaaa
cccc
bbbb
dddd
2
-6
7
0 2
9 3

17. 17
Cet algorithme permet de calculer le PCC d’un sommet «
s » à tous les autres sommets dans un graphe orienté de
longueur quelconque et aussi de détecter la présence d’un
circuit absorbant.
Soit λk(i) la valeur de chemin du sommet « s » vers le
sommet « i » ne contenant pas plus de k arcs, ainsi,
initialement : k = 0; λk (s) = 0 et λk(x) = ∞ pour x ≠s
Soit M l’ensemble des sommets dont le poids λk (s) a
été modifié à l’itération k, initialement il contient « s »
(M = {s} )
ALGORITHME DE FORD

18. 18
Tant qu’il existe un sommet marqué (M≠φ) et k est
inférieur ou égale à n (n présente le nombre des
sommets |X|) faire:
1. Incrémenter k
2. Initialiser l’ensemble NM à vide (NM contiendra les
sommet dont la marque λk sera modifiée)
ALGORITHME DE FORD

19. 19
3. Pour tout sommet x de Γ+(M) (i.e les successeurs des
sommets dont la marque a été modifié au cours de
l’itération k-1) faire:
a) Mettre à jour sa marque : λk (x) = min (λk-1 (x), λk
-1(y) +lyx) tel que y∈ Γ- (x) ∩ M
b) Si sa marque a été modifiée (λk (x) < λk-1 (x) ) alors
ajouter x à l’ensemble NM (NM = NM ∪ {x})
4. Remplacer M par MN
ALGORITHME DE FORD

20. 20
En absence de circuit absorbant dans le graphe,
l’algorithme se termine nécessairement à l’issue de
l’itération n (k = n) car, au pire des cas, le PCC de s
vers tous les autre sommets est un chemin élémentaire
possédant (n-1) arcs.
Si une ou plusieurs marques sont modifiées à l’itération
n (Γ+(M) ≠φ), cela signifie qu’il existe un circuit
absorbant.
ALGORITHME DE FORD

21. 21
Exemple 1: Trouver PCC de a vers tous les autres sommets
ALGORITHME DE FORD
k λk (a) λk (b) λk (c) λk (d) λk (e)
0 (init) 0 (*) ∞ ∞ ∞ ∞
1 0 3(*) 5(*)
2 9(*) 11(*) 5
3 (fin) 0 3 9 11 5
4
aaaa
bbbb
eeee
cccc
dddd
3
5
3
1 2
6
6
4
72

22. 22
Exemple 2: Trouver PCC de a vers tous les autres sommets
ALGORITHME DE FORD
k λk (a) λk (b) λk (c) λk (d) λk (e) λk (f)
0 (init) 0 (*) ∞ ∞ ∞ ∞ ∞
1 10(*) 2(*)
2 5(*) 7(*) -1(*)
3 -4(*) 6(*)
4 1(*) -2(*)
5 3(*) -5(*)
6 -8(*) 2(*)
aaaa
ffff
bbbb
eeee
-3
-3
-1
cccc
dddd
5
-510
2

23. 23
Cet algorithme permet de calculer le PCC entre tous les
couples de sommets dans un graphe orienté de longueur
quelconque et aussi de détecter la présence d’un circuit
absorbant.
Numéroter les sommets de 1 à n (|X| = n)
Soit la matrice A = {aij} de taille n x n définie initialement comme
suit:
ALGORITHME DE FLOYD

24. 24
Cet algorithme permet de calculer le PCC de la façon
suivante:
A la première itération, on cherche le PCC entre
chaque couple (i, j) passant éventuellement par le
sommet 1 ;
A l'itération k (avec k > 1), on cherche le PCC entre
chaque couple (i, j) passant par des sommets d'indice
inférieur ou égal à k.
ALGORITHME DE FLOYD

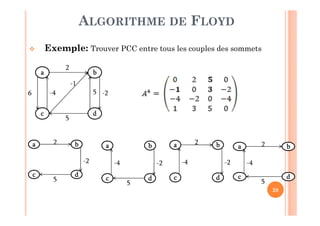
25. 25
Cet algorithme permet de calculer le PCC de la façon
suivante:
A l'itération n, la matrice An présente les valeurs du
PCC entre chaque couple (i, j).
S’il n’y a pas de circuit absorbant, ces valeurs sont
correctes.
S’il y a des circuits absorbants (de valeur négative),
ils sont détectés, puisque pour chaque sommet x
appartenant à un tel circuit, on aura A[x,x]<0.
ALGORITHME DE FLOYD

26. 26
Voici une description formelle de l'algorithme :
Pour tout sommet k (k allant de 1 à n)
Pour tout couple de sommet (i, j) calculer
ALGORITHME DE FLOYD
j
i
k
k

27. 27
Exemple: Trouver PCC entre tous les couples des sommets
ALGORITHME DE FLOYD
aaaa
cccc
bbbb
dddd
6
2
5
-1
-2-4 5

28. 28
Exemple: Trouver PCC entre tous les couples des sommets
ALGORITHME DE FLOYD
aaaa
cccc
bbbb
dddd
6
2
5
-1
-2-4 5
aaaa
cccc
bbbb
dddd
2
5
-2
aaaa
cccc
bbbb
dddd
5
-2-4
aaaa
cccc
bbbb
dddd
2
-2-4
aaaa
cccc
bbbb
dddd
2
5
-4

29. SOURCES DE CE COURS
Lucas Letocart, Cours d’Algorithmique de graphes, Institut Galilée,
Université Paris 13, Disponible sur www-galilee.univ-
paris13.fr/fichiers/Cours_Algo_Graphes.pdf
Laurent Canet, Algorithmique, graphes et programmation dynamique,
Notes de Cours & Rapport de Travaux Pratiques, 2003
Sana Aroussi, Notes des Travaux Dirigés de Recherche Opérationnelle,
Ecole nationale Supérieure d’Informatique (ESI), 2013.
Laurent Godefroy, Cours Théorie du graphe, Chapitre 03 - Algorithmes de
plus courts chemins, Université Internationale SUPINFO, disponible sur
https://www.supinfo.com/cours/2GRA/chapitres/03-algorithmes-plus-courts-
chemins#idm46133009494944
Jean-Michel Hélary, Le plus court chemin, 2005, Disponible sur
https://interstices.info/le-plus-court-chemin/
29