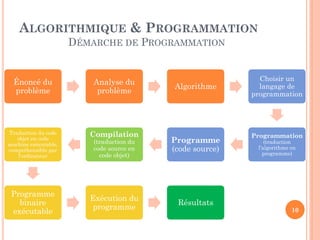
Le document présente un cours sur l'algorithmique pour les étudiants en licence de génie des systèmes informatiques, abordant des concepts tels que la récursivité, la complexité des algorithmes et les algorithmes de tri. Il décrit les objectifs du cours ainsi que le contenu, incluant les étapes de conception d'un algorithme et les qualités requises pour un bon algorithme. Des exemples pratiques illustrent la complexité des algorithmes et la nécessité de les évaluer avant leur implémentation.

1. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
Cours n°1: 9 Octobre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. PRÉAMBULE

Pré-requis: Cours (Algo1, S1) + (Algo 2, S2) + (Aglo 1, S4).

UEF: Algorithmique et Technologie d’Implémentation (ALTI)

Volume horaire hebdomadaire: 3H Cours + 1H30 TD

Évaluation: continu + Examen.

Coefficient 1, Crédit 4
2

3. OBJECTIFS DE LA MATIÈRE

Élaborer des algorithmes performants et efficaces

Comprendre la notion de complexité d’un algorithme

Maîtriser la récursivité (simple, multiple, mutuelle, imbriquée)

Savoir dé-récursiver des algorithmes simples et multiples

Maîtriser la démarche « diviser pour régner »

Savoir estimer la complexité d’un algorithme itératif ou récursif

Connaître les différents algorithmes de tri et estimer leur complexité

Comprendre la méthode gloutonne.

Définir la classe de complexité NP.

Étudier quelques algorithmes d’approximations de complexité polynomiale
(les heuristiques)
3

4. CONTENU DE LA MATIÈRE
I.
Introduction et Motivations
II.
Complexité et Optimalité
III.
Récursivité et Paradigme « diviser pour régner »
IV.
Algorithmes de tri
V.
Algorithmes gloutons
VI.
NP-complétude
VII.
Heuristiques
4

5. CHAPITRE I:
INTRODUCTION & MOTIVATION

6. PLAN DU CHAPITRE I
 Généralités
sur l’Algorithmique

Définition

Étapes de conception
 Algorithmique
et Programmation

Définition

Langages de programmation

Démarche de programmation
 Qualités
d’un Bon Algorithme
6

7. GÉNÉRALITÉ SUR L’ALGORITHMIQUE

Historique : L’algorithmique est un terme d’origine arabe,
hommage à Al Khawarizmi (780-850) auteur d’un ouvrage décrivant
des méthodes de calculs algébriques.

Définition:
Un
algorithme
est
suite
finie
d’opérations
élémentaires constituant un schéma de calcul ou de résolution d’un
problème.
7

8. GÉNÉRALITÉ SUR L’ALGORITHMIQUE
ÉTAPES DE CONCEPTION D’UN ALGORITHME
Analyse
Définition précise des données,
des traitements et de leur
séquencement
Définition du problème en terme
de séquences d’opérations de
calcul, de stockage de données
Conception
Programmation
Traduction et réalisation de
l’algorithme dans un langage
précis
8
Vérification du bon
fonctionnement de l’algorithme
Test

9. ALGORITHMIQUE & PROGRAMMATION

Définition : Un programme est la traduction d’un algorithme
dans un langage de programmation.
Langage
de haut
niveau
Binaire,
Assembleur
Langage
de bas
niveau
Évolution
Orienté Objet
(C++, C#, Java),
....
Procédural
(Pascal, C),
Logique (Prolog),
....
9

10. ALGORITHMIQUE & PROGRAMMATION
DÉMARCHE DE PROGRAMMATION
Énoncé du
problème
Analyse du
problème
Traduction du code
objet en code
machine exécutable,
compréhensible par
l'ordinateur
Compilation
Programme
binaire
exécutable
(traduction du
code source en
code objet)
Exécution du
programme
Algorithme
Programme
(code source)
Résultats
Choisir un
langage de
programmation
Programmation
(traduction
l’algorithme en
programme)
10

11. QUALITÉ D’UN BON ALGORITHME

Correct: Il faut que le programme exécute correctement ses
tâches pour lesquelles il a été conçu.

Complet: Il faut que le programme considère tous les cas
possibles et donne un résultat dans chaque cas.

Efficace: Il faut que le programme exécute sa tâche avec
efficacité, c’est-à-dire avec une complexité minimal qui s’est
mesurée en termes de temps de calcul et d’espace mémoire
nécessaire.
11

12. QUALITÉ D’UN BON ALGORITHME
EXEMPLE: CALCUL DE LA VALEUR D’UN POLYNÔME
Soit P(X) un polynôme de degré n
P(X) = anXn + an-1Xn-1 + ... + a1X + a0 ,
Où: n : entier naturel
an, an-1, ..., a1, a0 : les coefficients du polynôme

1ère variante
Début
1ère Complexité :
P0
(n+1) additions
Pour i allant de 0 à n faire
P  P+ ai *Xi
(n+1) multiplications
(n+1) puissances
Finpour
Fin
12

13. QUALITÉ D’UN BON ALGORITHME
EXEMPLE: CALCUL DE LA VALEUR D’UN POLYNÔME
1ère variante
Début
2ème variante
Début
Inter1
P0
Pour i allant de 0 à n faire
P  P+ ai
*Xi
Finpour
Fin
P 0
Pour i allant de 0 à n faire
P  P+ Inter *ai
Inter  Inter * X
finpour
1ère Complexité :
(n+1) additions
(n+1) multiplications
(n+1) puissances
Fin
2ème Complexité :
(n+1) additions
2(n+1) multiplications
13

14. QUALITÉ D’UN BON ALGORITHME
EXEMPLE: CALCUL DE LA VALEUR D’UN POLYNÔME
3ème variante: Schéma de Horner
P(X) = anXn + an-1Xn-1 + ... +a2X2 + a1X + a0
=(anXn-1 + an-1Xn-2 + ... +a2X + a1)X + a0
= ((anXn-1 + an-1Xn-2 + ... +a2)X+ a1)X + a0

= ............
=
(....(((anX + an-1)X+ an-2 )X.....)X+ ... +a2)X+ a1)X + a0
3ème variante
Début
P  an
Pour i allant de n-1 à 0 faire
P  P*X + ai
Finpour
Fin
3ème Complexité :
n additions
n multiplications
14

15. QUALITÉ D’UN BON ALGORITHME
EXEMPLE: CALCUL DE LA VALEUR D’UN POLYNÔME
Variantes
Première
Deuxième
Troisième
Complexité
(nombre
d’opérations)
(n+1) additions
(n+1) additions
n additions
(n+1) multiplications 2(n+1)
(n+1) puissances

Nécessité
d’estimer
n multiplications
multiplications
la
complexité
d’un
algorithme avant de l’écrire et l’implémenter
15

16. SOURCES DE CE COURS

Mohamed El Marraki, Algorithmique, Université Mohammed V-Agdal, Faculté des
Sciences Rabat, Département Mathématiques et Informatique, 2007, pp.35.
Disponible sur www.fsr.um5a.ac.ma/cours/informatique/elmarraki/Algo_ch1_3.pdf

Frédéric Vivien, Algorithmique avancée, École Normale Supérieure de Lyon, 2002.,
pp. 93. Disponible sur http://perso.ens-lyon.fr/frederic.vivien/Enseignement/Algo2001-2002/Cours.pdf

Slim Msfar,
Algorithmique
et Complexité, 2012,
pp
104.
Disponible sur
http://p835.phpnet.org/testremorque/upload/catalogue/coursalgorithmi.pdf
16