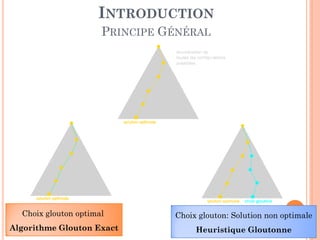
Le document présente un cours sur les algorithmes gloutons dans le cadre d'un enseignement en informatique, avec un focus sur les preuves d'optimalité et des exemples pratiques comme le problème du monnayeur et l'ordonnancement des tâches. Les algorithmes gloutons cherchent à construire des solutions optimales par des décisions locales sans revenir en arrière. Le cours détaille les concepts de choix glouton et de sous-structure optimale pour démontrer les conditions d'optimalité.

1. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE V:
ALGORITHMES GLOUTONS
Cours n°12: 24 Novembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. PLAN DU CHAPITRE V
 Introduction
 Schéma
 Preuve
Général
d’Optimalité
 Exemples
2

3. INTRODUCTION
PROBLÈME D’OPTIMISATION

On
est
souvent
dans
le
cadre
des
problèmes
d'optimisation:

E: un ensemble fini d'éléments.

S: une solution est construite à partir des éléments de E. Par
exemple: une partie de E, un multi-ensemble d'éléments de E, une
suite fini de E ou une permutation de E qui satisfait une certaine
contrainte.

A chaque solution S est associée une fonction objectif F(S).

Le but est de chercher une solution qui optimise (minimise ou
maximise) cette fonction objectif.
3

4. INTRODUCTION
PRINCIPE GÉNÉRAL

Pour un problème d’optimisation, un algorithme glouton
est un algorithme qui cherche à construire une
solution pas à pas

sans jamais revenir sur ses décisions,

en prenant à chaque étape la solution qui
semble la meilleure localement,

en espérant obtenir une solution optimale.
4

5. INTRODUCTION
PRINCIPE GÉNÉRAL
5
Choix glouton optimal
Choix glouton: Solution non optimale
Algorithme Glouton Exact
Heuristique Gloutonne

6. EXEMPLE 1: LE MONNAYEUR

On dispose des pièces de monnaie correspondant aux
valeurs E = {e1, ..., en}.

Pour chaque valeur ei, le nombre de pièces (nbi) est non
borné.

Étant donnée une somme « s » entière, on veut trouver
une façon de rendre la somme « s » avec un nombre de
pièces minimum.

Prendre E ={1, 10, 2, 5}, s = 28, Quelles la solution
optimale?
6

7. EXEMPLE 1: LE MONNAYEUR

Une solution S = (nb1, ...., nbn) présente le nombre de
pièces (nbi) pour chaque valeur (ei):



Elle est correcte si
Elle est optimale si
est minimal.
Algorithme glouton: Trier les valeurs de pièces par
ordre
décroissant.
Pour
chaque
valeur
de
pièce,
maximiser le nombre de pièces choisies.
7

8. EXEMPLE 1: LE MONNAYEUR
1ÈRE VERSION
Trier E en ordre décroissant
Pour i 1 à n faire
DP
S[i]  s div E[i]
s s mod E[i]
FP
8

9. SCHÉMA GÉNÉRAL

Il est basé sur un critère local de sélection des
éléments de E pour construire une solution optimale. En
fait, on travaille sur l'objet « solution partielle » et on
doit disposer des modules suivant:

Init qui initialise la solution de début

Select qui choisit le meilleur élément restant selon le
critère glouton: Souvent, on trie tout simplement la liste des
éléments selon le critère glouton au départ et on balaye
ensuite cette liste dans l'ordre.
9

10. SCHÉMA GÉNÉRAL

Init qui initialise la solution de début

Select qui choisit le meilleur élément restant selon le critère
glouton: Souvent, on trie tout simplement la liste des éléments
selon le critère glouton au départ et on balaye ensuite cette liste
dans l'ordre.

Complete? qui teste si une solution partielle est une solution
(complète).

AjoutPossible? qui teste si un élément peut être ajouté à une
solution partielle. Dans certains cas, c'est toujours vrai!

Ajout qui permet d'ajouter un élément à une solution si c'est
10
possible.

11. SCHÉMA GÉNÉRAL

L’algorithme Glouton est alors:
Trier (E)
Init (S)
Tant que Non Complete(S) faire
Select(x, E)
Si AjoutPossible(x) alors Ajout(S, x)
FTQ
11

12. EXEMPLE 1: LE MONNAYEUR
SCHÉMA GLOUTON
Trier (E) //en ordre décroissant
Init (S) //Initialiser la solution à 0 (nbi = 0)
i1
Tant que (i  n) faire // La solution est complète après
avoir parcouru tous les éléments de E
// Select retourne E(i)
// AjoutPossible est toujours vrai
S[i]  s div E[i] // Ajouter la solution
s s mod E[i]
i ++
FTQ
12

13. SCHÉMA GÉNÉRAL
COMPLEXITÉ

Soit n la cardinalité de E
Trier (E)
O (Ttrier ) = O(n log2 n)
Init (S)
TInit
Tcomplete
Tant que Non Complete(S) faire n fois
Select(x, E) Tselect
Si AjoutPossible(x) alors Ajout(S, x)
FTQ
Tpossible
f(n)
TAjout
13
La complexité est souvent de l’ordre O ( n log2 n + n f(n) )

14. EXEMPLE 1: LE MONNAYEUR
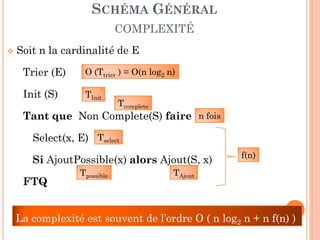
COMPLEXITÉ DU SCHÉMA GLOUTON
Trier (E)
Init (S)
i1
Tant que (i  n) faire
S[i]  s div E[i]
O (Ttrier) = O ( n log2 n )
s s mod E[i]
i ++
FTQ
14

15. SCHÉMA GÉNÉRAL
REMARQUES

Dans certains cas, le schéma général est encore plus
simple! Comme dans le cas de MONNAYEUR.

Dans d'autres cas, les solutions sont un peu plus
compliquées ... et on a besoin d'un schéma un peu plus
sophistiqué...
15

16. PREUVE D’OPTIMALITÉ

Un algorithme glouton produit des solutions optimales si
les propriétés suivantes sont vérifiées :
1. Propriété du choix glouton : Il existe toujours une
solution optimale qui contient un premier choix glouton

En général on montre que toute solution optimale contient ou
débute par le premier choix glouton.
16

17. PREUVE D’OPTIMALITÉ
2. Propriété de sous-structure optimale : toute solution
optimale contient une sous-structure optimale

Soit S une solution optimale du problème P contenant le choix C et
le S’ = S{C} alors S’ est une solution optimale du sous problème
PC résultant du choix C dans le problème P
17

18. PREUVE D’OPTIMALITÉ

Pour monter que l’algorithme glouton rend toujours une
solution optimale, il faut montrer que les deux
propriétés
(
choix
glouton
et
sous-structure
optimale) sont vérifiées.

Pour montrer que l’algorithme glouton ne rend pas
toujours une solution optimale, il suffit de trouver un
contre-exemple.
18

19. EXEMPLE 1: LE MONNAYEUR
PREUVE D’OPTIMALITÉ

E = {10 , 5, 2, 1}: Algorithme Glouton trouve toujours la
solution optimale?

Choix glouton : la valeur de pièce la plus grande

Si s ≥ 10 toute solution optimale contient au moins
une pièce de 10  c’est le premier choix glouton.

Si s < 10, l’algorithme fait un bon premier choix ( au
plus une pièce 5, au plus deux pièce de 2 et au plus
une pièce de 1)
Toute solution optimale contient donc un choix
19
glouton

20. EXEMPLE 1: LE MONNAYEUR
PREUVE D’OPTIMALITÉ

Propriété de sous-structure optimale :

Soient S une solution optimale pour la somme s et C  S
un choix glouton (la plus grande pièce) alors S’ = S- {C}
est une solution optimale pour s-valeur(C).

1ère Méthode: Preuve par absurde

Supposant que:

H1: S une solution optimale pour la somme s

H2: C  S un choix glouton (la plus grande pièce)

20
H3: S’ = S- {C} est une solution non optimale
pour s-valeur (C)

21. EXEMPLE 1: LE MONNAYEUR
PREUVE D’OPTIMALITÉ

1ère Méthode: Preuve par absurde

Supposant que:


H2: C  S un choix glouton (la plus grande pièce)


H1: S une solution optimale pour la somme s
H3: S’ est une solution non optimale pour s-valeur (C)
Alors il existe une solution S’’ meilleure que S’ pour svaleur (C), i.e.

Donc, S’’  {C} est meilleure que S’  {C} pour s car

21
i.e, S = S’  {C} n’est pas optimale (contradiction avec
l’hypothèse H1).

22. EXEMPLE 1: LE MONNAYEUR
PREUVE D’OPTIMALITÉ

E = {8, 4, 2}:

Solution optimale existe si S est pair et S >1

Algorithme Glouton donne la solution optimale si elle
existe

E = {5, 2}:



Solution optimale existe si n  4
Algorithme Glouton ne la trouve pas toujours (n=6)
E = {5, 4, 1}:

Solution optimale existe toujours

Algorithme Glouton trouve toujours la solution mais elle
22
n’est pas toujours optimale (n=8)

23. EXEMPLE 1: LE MONNAYEUR
PREUVE D’OPTIMALITÉ

Conclusion: Caractériser les jeux de pièces pour lesquels
l’algorithme glouton est optimal est un problème
ouvert. Il est facile de trouver des catégories qui
marchent (par exemple des pièces E ={1,B,B2,B3} pour B ≥
2) mais le cas général résiste !
23

24. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE V:
ALGORITHMES GLOUTONS
Cours n°13: 27 Novembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

25. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES

Soit E= {1,..., n} un ensemble de n tâches.

La tâche i commence à l’instant Di et finit à l’instant Fi.

Deux tâches i, j sont compatibles si elles ne se
chevauchent pas (Dj  Fi) .

But 1 : trouver un ensemble maximal de tâches
compatibles.
25

26. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
E
2
3
4
5
6
7
8
9
D
1
2
4
1
5
8
9
13
11
F

1
8
5
7
3
9
11
10
16
14
Algorithme glouton: Trier les tâches selon leur date
fin et sélectionner une tâche compatible par ordre
croissant.
26

27. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
E
1
2
3
4
5
6
7
8
9
D
1
2
4
1
5
8
9
13
11
F
8
5
7
3
9
11
10
16
14
1. Trier les tâches selon leur date fin
E
4
2
3
1
5
7
6
9
8
D
1
2
4
1
5
9
8
11
13
F
3
5
7
8
9
10
11
14
16
2. Sélectionner les tâches compatibles par ordre croissant
E
4
2
3
1
5
7
6
9
8
D
1
2
4
1
5
9
8
11
13
F
3
5
7
8
9
10
11
14
16
Solution: Tâches 4, 3, 7, 9
27

28. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
SCHÉMA GLOUTON
Trier (E, D, F) //trier selon ordre croissant de la date fin
S{E[1]}; j1 //Initialiser la solution
i2
Tant que (i  n) faire // La solution est complète après
avoir parcouru tous les éléments de E
// La tâche E[i] est sélectionnée
Si D[i]  F[j] // Si la tâche E[i] est compatible avec la
tâche E[j]
S S  {E[i]} // Ajouter la solution
j i;
i ++
FTQ
28

29. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Premier choix glouton : E[1] est la tâche ayant la
date fin la plus petite

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton

Soit S = { T1, ..., Tk} une solution optimale ordonnée
(D[T1] < D[T2]<.....<D[Tk]) tel que F[Tk]  F[1]

Si T1  E[1] alors S – {T1} contient l’ensemble des
tâches compatibles avec T1 ainsi avec E[1].

29
Ainsi, S – {T1}  {E[1]} est aussi une solution
optimale.

30. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Premier choix glouton : E[1] est la tâche ayant la
date fin la plus petite

Propriété 2: Toute solution optimale contient une
sous-structure optimale

Soit S = { T1, ..., Tm} une solution optimale ordonnée
(D[T1] < D[T2]<.....<D[Tk]) alors S – {T1} est aussi
une solution optimale. Le problème se ramène à
trouver une solution optimale des tâches compatibles
avec T1.
30

31. EXEMPLE 2: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Preuve par absurde

Supposant que:



H1: S = { T1, ..., Tk} une solution optimale
H2: S’ = S - {T1} est une solution non optimale.
Alors, il existe une solution meilleure (S’’) que S’, i.e.
|S’’| > |S’| = k-1.

Donc, S’’  {T1} est meilleure que S car |S’’  {T1}|> k,
i.e,
S
n’est
pas
l’hypothèse H1).
optimale
(contradiction
avec
31

32. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES

Soit E= {1,..., n} un ensemble de n tâches.

La tâche j commence à l’instant Di et finit à l’instant Fi.

Chaque tâche est exécutée sur une machine.

Une machine exécute une tâche à la fois.

But 2 : Trouver un nombre minimal de machines
permettant d’exécuter toutes les tâches.
32

33. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
E
2
3
4
5
6
7
8
9
D
1
2
4
1
5
8
9
13
11
F

1
8
5
7
3
9
11
10
16
14
Algorithme Glouton: Trier les tâches selon leur date
début et attribuer une machine compatible à chaque
tâche.
33

34. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
1. Trier les tâches selon leur date début
E
1
4
2
3
5
6
7
9
8
D
1
1
2
4
5
8
9
11
13
F
8
3
5
7
9
11
10
14
16
2. Attribuer une machine compatible à chaque tâche
E
1
4
2
3
5
6
7
9
8
D
1
1
2
4
5
8
9
11
13
F
8
3
5
7
9
11
10
14
16
M
1
2
3
2
3
2
1
3
1
Solution: 3 machines
34

35. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
SCHÉMA GLOUTON
Trier (E, D, F) //trier selon ordre croissant de la date
début
Soit FP une file prioritaire dans laquelle on garde les
machines. Les machines sont classés par ordre croissant
de la date fin de la tâche attribuée. Ainsi, une machine est
caractérisée par son numéro (Num) et une date fin (Fin).
CréerFile (FP); Nb0 //Initialiser la solution
i1
35

36. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
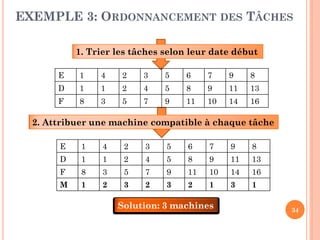
SCHÉMA GLOUTON
Trier (E, D, F) //trier selon ordre croissant de la date début
CréerFile (FP); Nb0; //Initialiser la solution
i1
Tant que (i  n) faire
Si (FP = Nil) ou (D[i] < FP.Fin)
// Si la file est vide ou la tâche E[i] est
compatible avec la machine FP.Num
NB++ // Ajouter la solution
M.Num  NB;
Sinon
Défiler (FP, M);
M.FinF[i]; Enfiler (FP, M)
i ++
FTQ
36

37. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Soit S = { M1, ..., Mk} une solution optimale.

Premier choix glouton : la tâche E[1], ayant la date
début la plus petite, est affectée à la machine M1

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton

La solution optimale contient au moins une machine
(k1), c’est la machine M1.
37

38. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Premier choix glouton : la tâche E[1], ayant la date
début la plus petite, est affectée à la machine M1

Propriété 2: Toute solution optimale contient une
sous-structure optimale

Soit S = { M1, ..., Mk} une solution optimale pour E
alors S – {M1} est aussi une solution optimale pour E
- {T(M1)}. T(M1) est l’ensemble des tâches exécutées
sur la machine M1.
38

39. EXEMPLE 3: ORDONNANCEMENT DES TÂCHES
PREUVE D’OPTIMALITÉ

Preuve par absurde

Supposant que:

H1: S = { M1, ..., Mk} une solution optimale pour E

H2: S’ = S- {M1} est une solution non optimale pour E –
{T(M1)}.

Alors, il existe une solution meilleure (S’’) que S’ pour E
– {T(M1)}, i.e. |S’’| < |S’| = k-1.

Donc, S’’  {M1} est meilleure que S pour E car
|S’’

{T1}|
<
k,
i.e,
S
n’est
(contradiction avec l’hypothèse H1).
pas
optimale
39

40. EXEMPLE 4: PROBLÈME DE SAC À DOS ENTIER

Soit E= {1,..., n} un ensemble de n objets.

Chaque objet i a un poids Pi et une valeur Vi. Il peut
être pris en entier et au plus une fois, i.e. Nbi  {0,
1}.

Soit un sac à dos de contenance maximale Pmax

But : Maximiser la valeur totale des objets mis
dans le sac à dos
40

41. EXEMPLE 4: PROBLÈME DE SAC À DOS ENTIER

Algorithme Glouton: trier les objets selon un critère
donné et sélectionner un objet jusqu’à atteindre la
capacité maximale de sac à dos.

Choix gloutons possibles

choisir l’objet de plus grande valeur

choisir l’objet le plus léger

choisir l’objet dont le rapport valeur/poids est
maximal.

41
Montrer que ces choix ne donnent pas de solution
optimale dans le cas où l’objet est pris en entier.

42. EXEMPLE 4: PROBLÈME DE SAC À DOS ENTIER
E
1
2
3
P
10
20
30
V
30
100
120
V/P
3
5
4
Pmax = 50
(220)
Pmax = 40
(150)
Pmax = 30
(130)
L’objet le plus
léger
Non (130)
Non (130)
Oui (130)
L’objet de plus
grande valeur
Oui (220)
Oui (150)
Non (120)
L’objet dont le
rapport V/P est
maximal
Oui (220)
Non (130)
Oui (130)
42

43. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 5 (3ème année)
ALGORITHMIQUE 02
CHAPITRE V:
ALGORITHMES GLOUTONS
Cours n°14: 01 Décembre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

44. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ

Soit E= {1,..., n} un ensemble de n objets.

Chaque objet i a un poids Pi et une valeur Vi. Il peut
être fractionné i.e. Nbi  [0, 1].

Soit un sac à dos de contenance maximale Pmax

But : Maximiser la valeur totale des objets mis
dans le sac à dos
44

45. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
E
1
2
3
P
10
20
30
V
30
100
120
V/P
3
5
4
Pmax = 50
(220)
Pmax = 40
(180)
Pmax = 30
(140)
L’objet le plus
léger
Non (210)
Non (170)
Non (130)
L’objet de plus
grande valeur
Oui (220)
Non (170)
Non (120)
Oui (180)
Oui (140)
L’objet dont le Oui (220)
rapport V/P
est maximal
45

46. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ

Une solution S = (nb1, ...., nbn) présente le nombre de
l’objet i (nbi  [0, 1])

Algorithme
glouton:
Trier
les
objets
par
ordre
décroissant de leur rapport Vi/Pi. Pour chaque objet,
maximiser le nombre nbi  [0, 1] jusqu’à atteindre la
capacité maximale de l’objet.
46

47. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
SCHÉMA GLOUTON
Trier (E, P, V) //trier selon ordre décroissant du rapport V/P
Init (S) //Initialiser la solution nbi à 0
i1
Tant que (Pmax > 0) et (i  n) faire
// Ajouter la solution
Si P[i]  Pmax
S[i]  1
Sinon
S[i]  Pmax / P[i]
Pmax  Pmax – P[i]
i ++
FTQ
47

48. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
PREUVE D’OPTIMALITÉ

Soit S = (nb1,..., nbn) une solution optimale.

Premier choix glouton : l’objet E[1], ayant le rapport
V/P le plus grand

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton
48

49. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
PREUVE D’OPTIMALITÉ

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton

Cette propriété est toujours vérifiée. En effet, il ne
peut exister que trois cas de figures:

S = (1, 1, ......, 1) si

S = (1, 1, ....., 1, k, 0, ....., 0) si

S = (1, 0, ....., 0) si
49

50. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
PREUVE D’OPTIMALITÉ

Soit S = (nb1,..., nbn) une solution optimale.

Propriété 2: Toute solution optimale contient une
sous-structure optimale

Soient S une solution optimale pour Pmax, alors S –
{nba} est aussi une solution optimale pour Pmax – Pa.
(Pa = nba x P[a])
50

51. EXEMPLE 5: PROBLÈME DE SAC À DOS FRACTIONNÉ
PREUVE D’OPTIMALITÉ

Preuve par absurde

Supposant que:

H1: S = (nb1,..., nbn) une solution optimale pour Pmax

H2: S’ = S- {nba} est une solution non optimale pour Pmax – Pa.

Alors, il existe une solution meilleure (S’’) que S’ pour
Pmax – Pa, i.e. W(S’’) > W(S’). W(K) retourne la valeur
totale de la solution K.

Donc, S’’  {nba} est meilleure que S pour Pmax car
V(S’’  {nba}) > V(S), i.e, S n’est pas optimale
51
(contradiction avec l’hypothèse H1).

52. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL

Soit G = (X,E, W) un graphe connexe non orienté valué
tel que:


E est l’ensemble des arrêtes avec |E| = m


X est l’ensemble de sommet avec |X| = n.
W est une fonction de valuation des arêtes W: ER
Un arbre recouvrant de G est un sous graphe A
(X, EA, W) connexe et sans cycle. Ainsi, | EA|= n-1.
52

53. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL

Un Arbre Recouvrant Mimimum ARmin (X,EA) du G est
un arbre recouvrant qui minimise
1.
2.
Écrire l’algorithme Glouton.
Prouver l’optimalité de l’algorithme
53

54. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL

Algorithme glouton: Trier les arêtes par ordre croissant
de leur valuation. Sélectionner une arête (si elle forme
pas un cycle avec les arêtes déjà sélectionnées) jusqu’à
construire un arbre recouvrant.

C’est le principe de l’Algorithme de Kruskal
54

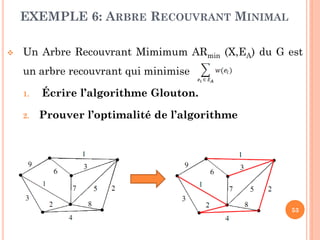
55. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL
SCHÉMA GLOUTON
Trier (E) //trier les arêtes selon ordre croissant de leur poids
Initi (EA)//Initialiser la solution; EA est un tableau à (n-1) éléments
nb0 // le nombre des arêtes sélectionnées
i 1
Tant que (nb n-1) faire
// la fonction Cycle vérifie que l’ensemble des arêtes EA  E[i] ne
forment pas un cycle
Si non Cycle (EA , E[i]) alors
nb ++
EA[nb]  E[i]
i ++
FTQ
55

56. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL
PREUVE D’OPTIMALITÉ

Premier choix glouton : l’arête e = E[1], ayant la
valuation la plus petite.

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton

Lemme 1: Soient A est un arbre recouvrant, e
A alors  e’  A tel que A – {e’}  {e} est un
arbre recourvrant. De plus, e’ peut être choisi
dans le cycle formé par les arêtes de A et e.
56

57. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL
PREUVE D’OPTIMALITÉ

Propriété 1: Il existe toujours une solution
optimale qui contient le premier choix glouton

Soit A la solution optimale.

Si e  A alors  e’  A tel que A – {e’}  {e} est aussi un
arbre recouvrant minimal. En effet

W(A – {e’}  {e}) = W (A) - w(e’) + w (e) = W* - w(e’) +
w (e) = W*

Ainsi, w (e) = w (e’), i.e. les deux arêtes possèdent 57
la
même valuation.

58. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL
PREUVE D’OPTIMALITÉ

Soit A* une solution optimale.

Propriété 2: Toute solution optimale contient une
sous-structure optimale

Soient A* une solution optimale pour W*, alors A*–
{e} est aussi une solution optimale pour W* - w (e)

Lemme 2: Soient A est un arbre recouvrant
pour G = (X, E) et e = (x, y) A tel que d(y) = 1
58
alors A – {e} est aussi un arbre pour G = (X – {y},
Ey)

59. EXEMPLE 6: ARBRE RECOUVRANT MINIMAL
PREUVE D’OPTIMALITÉ

Preuve par absurde

Supposant que:

H1: A* une solution optimale pour W*

H2: S’ = S- {e} est une solution non optimale pour W* – w(e).

Alors, il existe une solution meilleure (S’’) que S’ pour
W* – w(e), i.e. W(S’’) < W(S’).

Donc, S’’  {e} est meilleure que S pour Pmax car
V(S’’  {nba}) > V(S), i.e, S n’est pas optimale
(contradiction avec l’hypothèse H1).
59

60. SOURCES DE CE COURS

Sophie Tison, Algorithmes Gloutons (greedy algorithms), Cours Master Informatique
1ère année, Université Lille 1.

Chapitre 4 Algorithmes Gloutons, Cours MACS (Mathématiques Appliquées et Calcul
Scientifique), Disponible sur www.lamacs.fr/documents/cours/macs1/infochap4.pdf‎

Stéphane
Grandcolas,
Algorithmes
gloutons.
Disponible
sur
www.dil.univ-
mrs.fr/~gcolas/algo-licence/slides/gloutons.pdf‎

Yves Robert, Yves Caniou et Eric Thierry. Algorithmique - Cours et Travaux Dirigés,
École Normale Supérieure de Lyon, 2005.

Ana Busic, Algorithmes Gloutons, Conception d'algorithmes et applications, École
normale
supérieure,
Département
Informatique,
Disponible
sur
www.di.ens.fr/~busic/cours/LI325/slidesCAAC8_1213.pdf‎

Robert Cori, Analyse et Conception Algorithmes 1, Algorithmes gloutons, Disponible
sur www.lix.polytechnique.fr/~cori/Majeure/cours1.pdf‎
60