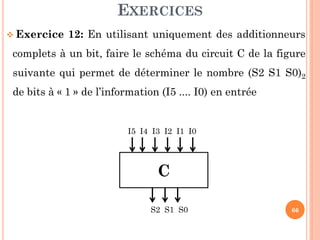
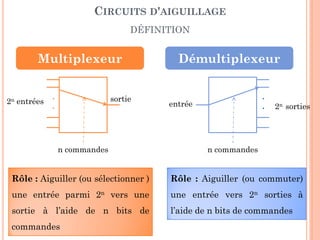
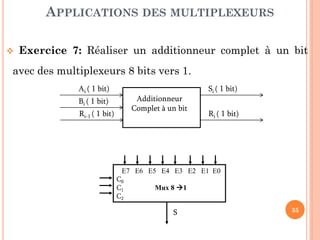
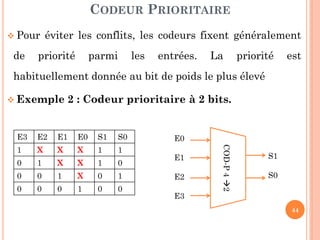
Ce document présente un cours sur la conception de circuits combinatoires, centré sur les additionneurs, soustracteurs et autres circuits arithmétiques utilisés dans le génie des systèmes informatiques. Il aborde des concepts tels que les demi-additionneurs, les additionneurs complets à un bit et à n bits, ainsi que des comparateurs et multiplexeurs. Les exercices proposés visent à renforcer la compréhension des circuits et leur mise en œuvre pratique.

1. Université Saad Dahleb de Blida
Faculté des Sciences
Département d’Informatique
Licence Génie des Systèmes Informatique (GSI)
Semestre 3 (2ème année)
CONCEPTION DE MACHINES DIGITALES
CHAPITRE II:
CIRCUITS COMBINATOIRES
Cours n°4-5: 20 Octobre 2013
AROUSSI Sana
Disponible sur https://sites.google.com/a/esi.dz/s-aroussi/

2. OBJECTIFS

Apprendre
la
structure
de
quelques
circuits
combinatoires souvent utilisés.

Apprendre comment utiliser des circuits combinatoires
pour concevoir d’autres circuits plus complexes.
2

3. INTRODUCTION

Les fonctions de sortie s’expriment selon des expressions logiques
des seules variables d’entrée.
3

4. PLAN DU CHAPITRE II
Circuits
arithmétiques
Circuit
d’aiguillage
Circuit de
transcodage
•Additionneur
•Soustracteur
•Multiplieur
•Diviseurs
• Comparaison
•UAL
•Multiplexeur
•Démultiplexeur
•Codeurs
•Décodeurs
•Transcodeurs
4

5. ADDITIONNEUR

Un additionneur est un circuit capable de faire l’addition de deux
nombre de n bits. Une addition génère deux résultats : la somme et la
retenue

Commençons par l’addition de deux bits Ai et Bi en entrée, avec en
sortie la somme Si et la retenue Ri.
Ai ( 1 bit)
Bi ( 1 bit)
Si ( 1 bit)
Demi-Additionneur
Ri ( 1 bit)
Rôle : Additionner Ai et Bi(Si = Ai + Bi) en conservant la retenue Ri

Cela s’appelle le demi-additionneur, parce qu’il ne tient pas compte
de la retenue qui peut aussi arriver en entrée, provenant de calculs
précédents.
5

6. DEMI-ADDITIONNEUR
Ai ( 1 bit)
Bi ( 1 bit)
Si ( 1 bit)
Demi-Additionneur
Ri ( 1 bit)
Rôle : Additionner Ai et Bi(Si = Ai + Bi) en conservant la retenue Ri

La table de vérité

Le schéma du circuit
Ai

Les équations Si = Ai Bi
Ri = Ai Bi,
XOR
Si
AND
Bi
Ri
6

7. ADDITIONNEUR COMPLET À UN BIT

En binaire, lorsqu’on fait une addition, il faut tenir en
compte de la retenue entrante :

L’additionneur complet à un bit permet de réaliser
l’addition de deux bits en tenant compte d’une retenue
Ri-1 en entrée.
7

8. ADDITIONNEUR COMPLET À UN BIT
Ri-1 ( 1 bit)
Ai ( 1 bit)
Bi ( 1 bit)
Si ( 1 bit)
Additionneur
Complet à un bit
Ri ( 1 bit)
Rôle : Additionner Ai et Bi en prenant en compte la retenue
d’entrée Ri-1 et en conservant la retenue de sortie Ri

La table de vérité

Les équations
Si  Ai .Bi .Ri 1  Ai .Bi .R i 1  Ai .B i .R i 1  Ai .Bi .Ri 1
Si  Ai .( Bi .Ri 1  Bi .R i 1 )  Ai .( B i .R i 1  Bi .Ri 1 )
Si  Ai ( Bi  Ri 1 )  Ai .( Bi  Ri 1 )
Si  Ai  Bi  Ri 1
8

9. ADDITIONNEUR COMPLET À UN BIT
Ri-1 ( 1 bit)
Si ( 1 bit)
Additionneur
Complet à un bit
Ai ( 1 bit)
Bi ( 1 bit)
Ri ( 1 bit)
Rôle : Additionner Ai et Bi en prenant en compte la retenue
d’entrée Ri-1 et en conservant la retenue de sortie Ri

La table de vérité

Les équations
Ri  Ai Bi Ri 1  Ai B i Ri 1  Ai Bi R i 1  Ai Bi Ri 1
Ri  Ri 1.( Ai .Bi  Ai .B i )  Ai Bi ( R i 1  i Ri 1 )
Ri  Ri 1.( Ai  Bi )  Ai Bi
9

10. ADDITIONNEUR COMPLET À UN BIT
Ri -1( 1 bit)
Ai ( 1 bit)
Bi ( 1 bit)
Si ( 1 bit)
Additionneur
Complet à un bit
Ri ( 1 bit)
Rôle : Additionner Ai et Bi en prenant en compte la retenue
d’entrée Ri et en conservant la retenue de sortie Ri+1

Le schéma
Ai
Bi
Ri-1
Si
Ri
10

11. ADDITIONNEUR COMPLET
Ri-1 ( 1 bit)
Ai ( 1 bit)
Bi ( 1 bit)
Si ( 1 bit)
Additionneur
Complet à un bit
Ri ( 1 bit)
Rôle : Additionner Ai et Bi en prenant en compte la retenue
d’entrée Ri-1 et en conservant la retenue de sortie Ri

Exercice 1: Faire le circuit de l’additionneur complet à
un bit en utilisant deux demi-additionneurs
11

12. ADDITIONNEUR COMPLET À UN BIT

Solution de l’exercice 1: Faire le circuit de l’additionneur complet
à un bit en utilisant deux demi-additionneurs
X et Y sont les sorties du
premier un demi
additionneur ayant comme
entrées A et B
Z et T sont les sorties du
deuxième additionneur
ayant comme entrées X et
Ri-1
12

13. ADDITIONNEUR COMPLET À UN BIT

Exercice 1: Faire le circuit de l’additionneur complet à un bit en
utilisant deux demi-additionneurs
13

14. ADDITIONNEUR COMPLET À N BITS PAR PROPAGATION
DE LA RETENUE
A ( n bit)
B ( n bit)
S ( n bit)
Additionneur
Complet à n bits
R ( 1 bit)
Rôle : Additionner A et B
14

15. ADDITIONNEUR COMPLET À N BITS PAR PROPAGATION
DE LA RETENUE

En utilisant les additionneurs complets à un bit :
Bn An
Rn-1
B3 A3
ACn
Rn
B2 A2
AC3
Sn
R3
B 1 A1
AC2
S3
R2
R0= 0
AC1
S2
R1
S1
15

16. SOUSTRACTEUR À N BITS
 Exercice
2:
Faire le circuit du soustracteur à N bits
Sachant que: A-B = A + CA2 (B)
= A + CA1 (B) + 1
16

17. MULTIPLIEUR À 4 BITS
 Exercice
3:
Faire le circuit de multiplieur complet à 4 bits
17

18. COURS N°6-7: 27 OCTOBRE 2013

19. COMPARATEUR À UN BIT
Ai ( 1 bit)
Bi ( 1 bit)
La table de vérité

A
fi ( 1 bit)
Comparateur à un
bit
fe ( 1 bit)
fs ( 1 bit)
Rôle : Comparer entre deux bits (A et B):
fe : égalité ( A=B)
fi : inférieur ( A < B)
fs : supérieur (A > B)

Les équations
B
fs
fe
fi
0
0
0
1
0
fs  A.B
0
1
0
0
1
fi  AB
1
0
1
0
0
fe  AB  AB  A  B  fs  fi
1
1
0
1
0
19

20. COMPARATEUR À UN BIT
Ai ( 1 bit)
Bi ( 1 bit)
fi ( 1 bit)
Comparateur à un
bit
fe ( 1 bit)
fs ( 1 bit)
Rôle : Comparer entre deux bits (A et B):
fs  A.B
fi  AB
fe  AB  AB  A  B  fs  fi
A
fs
fe
B
fi
20

21. COMPARATEUR À 2 BITS
Ai ( 2 bit)
Bi ( 2 bit)
fi ( 1 bit)
Comparateur à 2
bit
fe ( 1 bit)
fs ( 1 bit)
Rôle : Comparer entre deux nombres à 2 bits (A et B):
fe : égalité ( A=B)
fi : inférieur ( A < B)
fs : supérieur (A > B)
 Exercice
4:
Réaliser un tel circuit en utilisant des minimum
de portes logiques.
21

22. COMPARATEUR À 2 BITS
A2
A1
B2
B1
fs fe fi
0
0
0
0
0
1
0
0
0
0
1
0
0
1
0
0
1
0
0
0
1
0
0
1
1
0
0
1
0
1
0
0
1
0
0
0
1
0
1
0
1
0
0
1
1
0
0
0
1
0
1
1
1
0
0
1
1
0
0
0
1
0
0
1
0
0
1
1
0
0
1
0
1
0
0
1
0
1
0
1
1
0
0
1
1
1
0
0
1
0
0
1
1
0
1
1
0
0
1
1
1
0
1
0
0
1
1
1
1
0
1
0
1. A=B si A2=B2 et
A1=B1
fe  ( A2  B2).( A1  B1)
2. A>B si A2 > B2 ou
(A2=B2 et A1>B1)
fs  A2.B2  ( A2  B2).( A1.B1)
3. A<B si A2 < B2 ou
(A2=B2 et A1<B1)
22
22
fi  A2.B2  ( A2  B2).( A1.B1)

23. COMPARATEUR À 2 BITS
Ai ( 2 bit)
Bi ( 2 bit)
fi ( 1 bit)
Comparateur à 2
bit
fe ( 1 bit)
fs ( 1 bit)
Rôle : Comparer entre deux nombres à 2 bits (A et B):
fe : égalité ( A=B)
fi : inférieur ( A < B)
fs : supérieur (A > B)
 Exercice
5:
Réaliser un tel circuit en utilisant des
comparateurs à 1 bit
23

24. a2 b2
COMPARATEUR À 2 BITS
Comparateur 1 bit
fs2 fe2 fi2
a1
b1
Comparateur 1 bit
fs1 fe1 fi1
1. A=B si A2=B2 et A1=B1
fe  (A2  B2).(A1 B1)  fe2.fe1
2. A>B si A2 > B2 ou (A2=B2 et A1>B1)
fs  A2.B2  (A2  B2).(A1.B1)  fs2  fe2.fs1
3. A<B si A2 < B2 ou (A2=B2 et A1<B1)
fi  A2.B2  (A2  B2).(A1.B1)  fi2  fe2.fi1
24

25. COMPARATEUR À 2 BITS
a2
a1
b2
Comparateur 1 bit
fs2
fe2
b1
Comparateur 1 bit
fi2
fs1
fe1
fi1
25
fs
fe
fi

26. COMPARATEUR AVEC DES ENTRÉES DE MISE
EN CASCADE

On remarque que :



Si A2 >B2 alors A > B
Si A2<B2 alors A < B
Par contre si A2=B2 alors il faut tenir en compte du résultat de la
comparaison des bits du poids faible.

Pour cela, on rajoute au comparateur des entrées qui nous
indiquent le résultat de la comparaison précédente.

Ces entrées sont appelées des entrées de mise en cascade.
26

27. COMPARATEUR À UN BIT AVEC DES ENTRÉES DE MISE
EN CASCADE
A
A>B
B
Es Eg Ei
fs fe fi
X
1
X
X
0
A
B
0
Comp
A<B
X
X
0
0
1
1
A=B
X
0
0
1
0
0
0
1
0
0
1
0
0
0
1
0
0
1
Es ( >)
Eg ( =)
Ei ( <)
fs fe fi
fs= (Ai>Bi) ou (Ai=Bi).Es
fi= ( Ai<Bi) ou (Ai=Bi).Ei
fe= (Ai=Bi).Eg
27

28. COMPARATEUR À DEUX BITS AVEC DES ENTRÉES DE MISE
EN CASCADE

Exercice 6: Réaliser un comparateur à deux bits en
utilisant des comparateurs à un bit avec des entrées de
mise en cascade?
b2
a2
b1
a1
‘0’
Comp
Comp
Es
Es
Eg
fs2
fe2
fi2
Ei
Eg
fs1
fe1
fi1
‘1’
Ei
28

29. COMPARATEUR À N BITS AVEC DES ENTRÉES DE MISE EN
CASCADE
Bn
An
Bn-1
An-1
B1
A1
‘0’
Compn
fsn fen fin
fs
fe
fi
Esn
Egn
Ein
Compn-1
Comp1
fsn-1fen-1fin-1
fs1 fe1 fi1
‘1’
29

30. CIRCUITS D'AIGUILLAGE
DÉFINITION
Multiplexeur
2n entrées
.
.
sortie
n commandes
Démultiplexeur
.
.
entrée
2n sorties
n commandes
Rôle : Aiguiller (ou sélectionner )
Rôle : Aiguiller (ou commuter)
une entrée parmi 2n vers une
une entrée vers 2n sorties à
sortie à l’aide de n bits de
l’aide de n bits de commandes30
commandes

31. MULTIPLEXEUR 2 BITS VERS 1
C0
S
0
E0
E1 E0
C0
1
Mux 2 1
E1
S
S  C0 .E 0  C0 .E1
31

32. MULTIPLEXEUR 4 BITS VERS 1
C1
C0
S
0
0
E0
0
1
E1
1
0
1
E3
C0
C1
E2
E1 E0
Mux 4 1
E2
1
E3
S
S  C1.C 0.( E 0)  C1.C 0.( E1)  C1.C 0.( E 2)  C1.C 0.( E3)
32

33. MULTIPLEXEUR 4 BITS VERS 1

Vérifier que le multiplexeur 41 peut aussi être obtenu
avec trois multiplexeurs 2 de la façon suivante :
C1
C0
S1 S2 S3
0
0
E0 E2 E0
0
1
E1 E3 E1
1
0
E0 E2 E2
1
1
E1 E3 E3
E3 E2
C0
E1 E0
M1
M2
S2
C1
S1
M3
33

34. APPLICATIONS DES MULTIPLEXEURS

Conversion parallèle/série : aiguiller les informations
présentées en parallèle à l’entrée du MUX en des
informations de type série en sortie.
 „ Réalisation
de fonctions logiques : toute fonction
logique de N variables est réalisable avec un multiplexeur
de 2N vers 1
34

35. APPLICATIONS DES MULTIPLEXEURS

Exercice 7: Réaliser un additionneur complet à un bit
avec des multiplexeurs 8 bits vers 1.
Ai ( 1 bit)
Si ( 1 bit)
Additionneur
Complet à un bit
Bi ( 1 bit)
Ri-1 ( 1 bit)
Ri ( 1 bit)
E7 E6 E5 E4 E3 E2 E1 E0
C0
C1
C2
Mux 8 1
S
35

36. MULTIPLEXEUR 8 BITS VERS 1
C2
C1
C0
S
0
0
0
E0
0
0
1
E1
0
1
0
E2
0
1
1
E3
C0
C1
1
0
0
E4
C2
1
0
1
E5
1
1
0
E6
1
1
1
E7
E7 E6 E5 E4 E3
E2
E1 E0
Mux 8 1
S  C 2.C1.C 0.( E 0)  C 2.C1.C 0( E1)  C 2.C1.C 0( E 2)  C 2.C1.C 0( E 3) 
C 2.C1.C 0( E 4)  C 2.C1.C 0( E 5)  C 2.C1.C 0( E 6)  C 2.C1.C 0( E 7)
36

37. APPLICATIONS DES MULTIPLEXEURS
Ai Bi Ri-1 Si
0
0
0
0
E0
0
0
1
1
E1
0
1
0
1
E2
0
1
1
0
E3
1
0
0
1
E4
1
0
1
0
E5
1
1
0
0
E6
1
1
1
1
‘1’
‘0’
Si
Ri-1
Bi
Ai
E7 E6 E5 E4 E3
E2
E1 E0
E7
C0 C1 C2
Mux 8 1
Si
S i  Ai .B i .R i 1 (0)  Ai .Bi .Ri 1 (1)  Ai .Bi .R i 1 (1)  Ai .Bi .Ri 1 (0)  Ai .B i .R i 1 (1)  Ai .B i .Ri 1 (0)
 Ai .Bi .R i 1 (0)  Ai .Bi .Ri 1 (1)

38. APPLICATIONS DES MULTIPLEXEURS
Ai Bi Ri-1 Ri
0
0
0
0
E0
0
0
1
0
E1
0
1
0
0
E2
0
1
1
1
E3
1
0
0
0
E4
1
0
1
1
E5
1
1
0
1
E6
1
1
1
1
‘1’
‘0’
Ri
Ri-1
Bi
Ai
E7 E6 E5 E4 E3
E2
E1 E0
E7
C0 C1 C2
Mux 8 1
Ri
Ri  Ai B i R i 1 .(0)  Ai B i Ri 1 .(0)  Ai Bi R i 1 .(0)  Ai Bi Ri 1 .(1)  Ai B i R i 1 .(0)  Ai B i Ri 1 .(1)
 Ai Bi R i 1 .(1)  Ai Bi Ri 1 .(1)

39. DÉMULTIPLEXEUR

Le démultiplexeur joue le rôle inverse d’un multiplexeur.
Il permet de faire passer une information dans l’une des
sorties selon les valeurs des entrées de commandes.
E1
E2
.
.
E 2n
S1
.
.
.
.
S
MUX
E
DEMUX
.
.
.
S2
.
.
S2n
39

40. DÉMULTIPLEXEUR 4 BITS VERS 1
E
C1
C0
S3 S2
S1
S0
C0
C1
DEMUX 1 4
S3
S2
S1
S0
0
0
0
0
0
E
0
1
0
0
E
0
1
0
0
E
0
0
S 0  C1.C 0.( E )
1
1
E
0
0
0
S1  C1.C 0.( E )
S 2  C1.C 0.( E )
S 3  C1.C 0.( E )
40

41. CIRCUIT DE TRANSCODAGE
DÉFINITION

Un circuit de transcodage transforme une information
présente en entrée sous une forme donnée (code 1) en la
même information présente en sous une forme différente
(code 2).
Code 1
Circuit de
Code 2
Transcodage
41

42. CIRCUIT DE TRANSCODAGE
TYPES
42

43. CODEUR BINAIRE

Le codeur (ou encodeur) binaire (ou élémentaire) possède
2n entrées dont une seule est activée à la fois. Il fournit en
sortie le numéro de l’entrée active (sur n bit).

Exemple 1 : Codeur élémentaire à 2 bits
E2
E1
E0
S1
S0
1
0
0
0
1
1
0
1
0
0
1
0
0
0
1
0
0
1
0
0
0
1
0
0
E0
E1
E2
COD 4 2
E3
S1
S0
E3
43

44. CODEUR PRIORITAIRE
 Pour
de
éviter les conflits, les codeurs fixent généralement
priorité
parmi
les
entrées.
La
priorité
est
habituellement donnée au bit de poids le plus élevé
 Exemple
2 : Codeur prioritaire à 2 bits.
E2
E1
E0
S1
S0
1
X
X
X
1
1
0
1
X
X
1
0
0
0
1
X
0
1
0
0
0
1
0
0
E0
E1
E2
E3
COD-P 4 2
E3
S1
S0
44

45. DÉCODEUR

Le décodeur possède n entrées et 2n sorties dont une
seule sortie est activée à la fois. Il est souvent doté d’une
entrée de validation « V » qui sert à valider son
fonctionnement.
Exemple 1 : Décodeur binaire (ou élémentaire) à 2 bits qui
active la sortie correspond au numéro de l’entrée.
V
E1 E0 S3
S2
S1
0
X
X
0
0
0
0
1
0
0
0
0
0
1
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
1
0
0
S0
S0
0
E1
E0
DEC 2 4

S1
S2
S3
V
45

46. DÉCODEUR 2  4
Exemple 1 : Décodeur binaire (ou élémentaire) à 2 bits qui
active la sortie correspond au numéro de l’entrée.
V
E1 E0 S3
S2
S1
S0
0
X
X
0
0
0
0
1
0
0
0
0
0
1
1
0
1
0
0
1
0
1
1
0
0
1
0
0
1
1
1
1
0
0
S0
0
E1
E0
DEC 2 4

S1
S2
S3
V
S 0  ( E1.E0 ).V
S1  ( E1.E0 ).V
S 2  ( E1.E0 ).V
S 3  ( E1.E0 ).V
46

47. DÉCODEUR 3  8
S0
S1
S2
S3
S4
S5
S6
S7
E0
E1
V
E2
E1
E0
S0
0
X
X
X
1
0
0
1
0
1
S1
E2
S2
S3
S4
S5
S6
S7
0 0
0
0
0
0
0
0
0
1 0
0
0
0
0
0
0
0
1
0 1
0
0
0
0
0
0
0
1
0
0 0
1
0
0
0
0
0
S1  V ( E2 .E1.E0 )
1
0
1
1
0 0
0
1
0
0
0
0
S 2  V ( E2 .E1.E0 )
1
1
0
0
0 0
0
0
1
0
0
0
S 3  V ( E2 .E1.E0 )
1
1
0
1
0 0
0
0
0
1
0
0
S 4  V ( E2 .E1.E0 )
1
1
1
0
0 0
0
0
0
0
1
0
S 5  V ( E2 .E1.E0 )
1
1
1
1
0 0
0
0
0
0
0
1
S 6  V ( E2 .E1.E0 )
V
S 0  V ( E2 .E1.E0 )
S 7  V ( E2 .E1.E0 )
47

48. DÉCODEUR 4  16
ACCROISSEMENT DE CAPACITÉ PAR ASSOCIATION DE CIRCUITS

Exercice 8 : Réaliser un décodeur binaire à 4 bits en utilisant des
décodeur à 2 bits.
S0
S1
E0
E1
E2
E3
.
.
.
S15
V
48

49. V
E2
E1 E0 Sortie Activé
0
X
X
X
X
Aucune
1
0
0
0
0
S0
1
0
0
0
1
S1
1
5ème
décodeur
pour
sélectionner
un des
quatre
décodeurs
E3
0
0
1
0
S2
1
0
0
1
1
S3
1
0
1
0
0
S4
1
0
1
0
1
S5
1
0
1
1
0
S6
1
0
1
1
1
S7
1
1
0
0
0
S8
1
1
0
0
1
S9
1
1
0
1
0
S10
1
1
0
1
1
S11
1
1
1
0
0
S12
1
1
1
0
1
S13
1
1
1
1
0
S14
1
1
1
1
1
S15
1er décodeur
2ème décodeur
3ème décodeur
4ème décodeur
49

50. DÉCODEUR 4  16
ACCROISSEMENT DE CAPACITÉ PAR ASSOCIATION DE CIRCUITS

Exercice 8 : Réaliser un décodeur binaire à 4 bits en utilisant des
décodeur à 2 bits.
E2 E3
V
E1 E0
E1 E0
Sélectionner un des 4 décodeurs
V0 V1 V2 V3
E1 E0
E1 E0
50
S0 S1 S2 S3
S4 S5 S6 S7
S8 S9 S10 S11
S12 S13 S14 S15

51. DÉCODEUR 4  16
ACCROISSEMENT DE CAPACITÉ PAR ASSOCIATION DE CIRCUITS

Exercice 9 : Réaliser un décodeur binaire à 4 bits en utilisant des
décodeur à 3 bits.
S0
S1
E0
E1
E2
E3
.
.
.
S15
V
51

52. V
E2
E1 E0 Sortie Activé
0
X
X
X
X
Aucune
1
0
0
0
0
S0
1
0
0
0
1
S1
1
Le bit E3
sélectionne
les sorties
de décodeur
qui doit être
actif
E3
0
0
1
0
S2
1
0
0
1
1
S3
1
0
1
0
0
S4
1
0
1
0
1
S5
1
0
1
1
0
S6
1
0
1
1
1
S7
1
1
0
0
0
S8
1
1
0
0
1
S9
1
1
0
1
0
S10
1
1
0
1
1
S11
1
1
1
0
0
S12
1
1
1
0
1
S13
1
1
1
1
0
S14
1
1
1
1
1
S15
1er décodeur
2ème décodeur
52

53. DÉCODEUR 4  16
ACCROISSEMENT DE CAPACITÉ PAR ASSOCIATION DE CIRCUITS

Exercice 9 : Réaliser un décodeur binaire à 4 bits en utilisant des
décodeur à 3 bits.

Solution: deux décodeurs traitent en parallèle les bits E2, E1, E0.
Le bit E3 sélectionne les sorties de décodeur qui doit être actif
E3
E2 E1 E0
S0 S1 S2 S3 S4 S5 S6 S7
E2 E1 E0
S8 S9 S10 S11 S12 S13 S14 S15
53

54. COURS N°8-9: 3 NOVEMBRE 2013

55. APPLICATIONS DES DÉCODEURS
U.A.L

Un décodeur est un dispositif essentiel à l’entrée de
l’Unité Logique et Arithmétique (UAL) du processeur.

Exemple d’une version simplifiée d’UAL à un bit:
Cette UAL possède deux entrées (A, B) à un bit sur
lesquelles quatre opérations sont faites:

NON A,

A ET B,

A OU B

A + B (addition arithmétique).
55

56. APPLICATIONS DES DÉCODEURS
A
U.A.L
B
NOT
Non A
ET
A et B
ET
ET
S
OU
OU
A ou B
ET
D-A
A+B
ET
S0 S1 S2 S3
Décodeur
C0
C1
56

57. APPLICATIONS DES DÉCODEURS
MÉMOIRE PRINCIPALE

Un décodeur est un dispositif essentiel à l’entrée de la
mémoire principale.
Mémoire Principale
2n sorties
Contenu
0
2
12
.
.
.
.
.
.
28
2n
Décodeur
21
2n-1
Sélectionner
un mot
mémoire
23
1
n entrées
Bus
d’adresse
N° ligne
31
57

58. APPLICATIONS DES DÉCODEURS
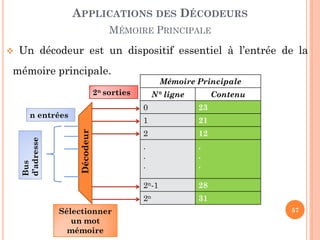
MÉMOIRE PRINCIPALE

Exemple: Sélectionner une cellule (colonne) [L, C] de la
mémoire principale.
0
1
Décodeur
(L)2
2
.
.
.
.
.
.
2n-1
(1)
Sélectionner
la ligne
2n
(C)2
Multiplexeur
(2)
58
Sélectionner
la colonne

59. TRANSCODEUR
 Un
transcodeur est un dispositif qui permet de faire
passer une information écrite dans le code C1 à un autre
Code C2.
 Les
deux importantes applications de transcodeurs sont:
 la conversion de code

l’affichage par segment
59

60. TRANSCODEUR BCD/XS3
 Exercice
10: Réaliser un transcodage du code BCD vers
le code à excès de trois (SX3(N) = BCD(N) + 3). Les
nombres d’entrée et de sortie sont exprimés sur 4 bits, et
ce transcodeur pourra convertir tous les chiffres de 0 à 9.
60

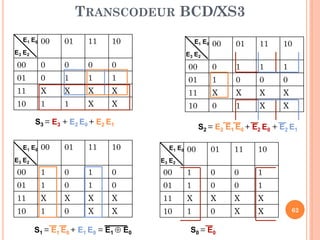
61. TRANSCODEUR BCD/XS3
Chiffre
converti
Entrées (BCD)
E3
E2
Sorties [XS 3]
E1
E0
S3
S2
S1
S0
0
0
0
0
0
0
0
1
1
1
0
0
0
1
0
1
0
0
2
0
0
1
0
0
1
0
1
3
0
0
1
1
0
1
1
0
4
0
1
0
0
0
1
1
1
5
0
1
0
1
1
0
0
0
6
0
1
1
0
1
0
0
1
7
0
1
1
1
1
0
1
0
8
1
0
0
0
1
0
1
1
9
1
0
0
1
1
1
0
0
-
1
0
1
0
x
x
x
x
-
1
0
1
1
x
x
x
x
-
1
1
0
0
x
x
x
x
-
1
1
0
1
x
x
x
x
-
1
1
1
0
x
x
x
x
-
1
1
1
1
x
x
x
x
61

62. TRANSCODEUR BCD/XS3
E1 E0
00
01
11
10
E1 E0
E3 E2
00
01
11
10
E3 E2
00
0
0
0
0
00
0
1
1
1
01
0
1
1
1
01
1
0
0
0
11
X
X
X
X
11
X
X
X
X
10
1
1
X
X
10
0
1
X
X
S3 = E3 + E2 E0 + E2 E1
E1 E0
00
01
11
10
E3 E2
S2 = E2 E1 E0 + E2 E0 + E2 E1
E 1 E0
00
01
11
10
E3 E2
00
1
0
1
0
00
1
0
0
1
01
1
0
1
0
01
1
0
0
1
11
X
X
X
X
11
X
X
X
X
10
1
0
X
X
10
1
0
X
X
S1 = E1 E0 + E1 E0 = E1  E0
S0 = E0
62

63. TRANSCODEUR HEXA/7 SEGMENTS
 Exercice
11: Les 16 chiffres 0-9 et A-F sont affichés au moyen d’un
dispositif appelé afficheur à 7 segments. Cet afficheur est un ensemble
de diodes électroluminescentes (D.E.L) disposés comme le montre la
figure suivante:
S0
E0
E1
E2
E3
Hexa/7 Segments
S0
S1
S2
S3
S4
S5
S6
S1
S6
S5
S2
S4
S3
63

64. TRANSCODEUR HEXA/7 SEGMENTS
S0
E0
E1
E2
E3
Hexa/7 Segments
S0
S1
S2
S3
S4
S5
S6
S1
S6
S5
S2
S4
S3
64

65. AFFICHEUR 7 SEGMENTS
Chiffre
converti
Entrées
E3
E2
E1
Sorties
E0
S6
S5
S4
S3
S2
S1
S0
0
0
0
0
0
1
0
1
1
1
1
1
1
0
0
0
1
1
0
1
0
0
0
0
2
0
0
1
0
1
1
0
1
1
0
1
3
0
0
1
1
1
1
1
1
0
0
1
4
0
1
0
0
1
1
1
0
0
1
0
5
0
1
0
1
0
1
1
1
0
1
1
6
0
1
1
0
0
1
1
1
1
1
1
7
0
1
1
1
1
0
1
0
0
0
1
8
1
0
0
0
1
1
1
1
1
1
1
9
1
0
0
1
1
1
1
1
0
1
1
A
1
0
1
0
1
1
1
0
1
1
1
B
1
0
1
1
0
1
1
1
1
1
0
C
1
1
0
0
0
0
0
1
1
1
1
D
1
1
0
1
1
1
1
1
1
0
E
1
1
1
0
0
1
0
1
1
1
0 65
1
F
1
1
1
1
0
1
0
0
1
1
1

66. EXERCICES
 Exercice
12: En utilisant uniquement des additionneurs
complets à un bit, faire le schéma du circuit C de la figure
suivante qui permet de déterminer le nombre (S2 S1 S0)2
de bits à « 1 » de l’information (I5 .... I0) en entrée
I5 I4 I3 I2 I1 I0
C
S2 S1 S0
66

67. EXERCICES
 Exercice
13: On veut afficher le résultat de la
comparaison de deux nombre binaire A (4 bits) et B (4 bits)
avec un afficher 7 segment. Étudier le circuit qui permet de
rendre lumineux les segments de façon à écrire
S0
S0
S1
S1
S5
S5
Si A > B
S4
S1
S2
Si A = B
Si A < B
S2
67
S3
S3

68. EXERCICES
 Exercice
14: En se basant sur l’algorithme et les exemples donnés
en fin d’exercice, proposer à base d’un minimum de circuits
combinatoires et de portes logiques, le schéma de réalisation d’une
additionneur de deux nombres positifs A (4 bits) et B (4 bits) exprimés
en code BCD (Binary Coded Decimal).
68

69. EXERCICES
 Exercice
14: En se basant sur l’algorithme et les exemples donnés
en fin d’exercice, proposer à base d’un minimum de circuits
combinatoires et de portes logiques, le schéma de réalisation d’une
additionneur de deux nombres positifs A (4 bits) et B (4 bits) exprimés
en code BCD (Binary Coded Decimal).
69

70. SOURCES DE CE COURS

Cours d’Architecture des ordinateurs, École nationale Supérieure d’Informatique
(ESI), Alger, Année universitaire 2011/2012.

Michel Jézéquel, Cours 2 « Circuits combinatoires », 2009. Disponible sur
public.enst-bretagne.fr/~douillar/ELP304/Cours2.pdf

Partie
3:
logique
Combinatoire
.
Disponible
sur
ensa-mecatronique.e-
monsite.com/medias/files/cours-elec-num-3.pdf

Cours
4
:
Circuits
combinatoires.
Disponible
sur
http://www.ief.u-
psud.fr/~roger/Enseigne/DUT_S2_Info_Instrum/09_C4_Logique_combinatoire.pdf

Pierre
Audibert,
VII-
Circuits
combinatoires
élémentaires,
disponible
sur
http://www.ai.univ-paris8.fr/~audibert/ens/7-CIRCUITS%20COMBINATOIRES.pdf

Pierre
Marchand,
Unité
4:
Logique
combinatoire,
www.ift.ulaval.ca/~marchand/ift17583/Acetates/17583-Acetates04.pdf‎
.
2001,
70