Le document traite de la complexité des algorithmes en géométrie algorithmique, un domaine important dans divers secteurs comme la robotique et le design industriel. Il explore des concepts fondamentaux tels que l'enveloppe convexe et des techniques comme le 'divide-and-conquer' et la recherche binaire pour résoudre des problèmes géométriques. Enfin, des théorèmes généraux sont présentés pour calculer la complexité de ces algorithmes.

1. La complexité des
algorithmes récursives
Géométrie algorithmique
Hajer TRABELSI
Master de recherche MR1-IMD/ISAMM
Juin 2014
1

2. Contexte
 Aujourd'hui la complexité est devenue un élément important
2
dans plusieurs domaine.
 Géométrie algorithmique est un domaine relativement récent né
autour des années 70s, dont le but est d'étudier les propriétés
des objets géométriques.
 Elle joue un rôle fondamental dans un grand nombre de
domaines tels que le robotique, conception assistée par
ordinateur, " design" industriel, image de synthèse, jeux vidéo...
 Cela explique l’importance algorithmique des problèmes
géométriques.
 Nous nous intéressons de la complexité des algorithmes
dans ce domaine.
La complexité des algorithmes récursives
Géométrie algorithmique

3. Plan
 Géométrie algorithmique
 Enveloppe convexe
 Algorithmes
3
 Diviser pour régner (Divide-and-conquer)
 Recherche Binaire (Binary search)
 Théorèmes générales
 Conclusion
La complexité des algorithmes récursives
Géométrie algorithmique

4. Géométrie algorithmique
 C’est le domaine qui traite des algorithmes manipulant
des concepts géométriques.
 « C’est l'art d'accommoder ensemble les objets
géométriques élémentaires pour en faire des objets plus
élaborés. » - Olivier Devillers - [10]
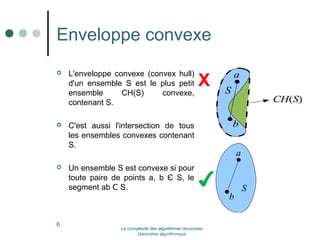
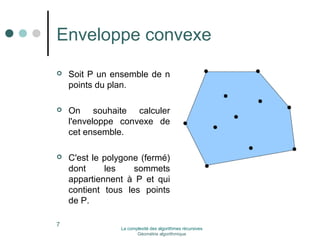
 L'exemple le plus cité étant celui de l'enveloppe
convexe : on a au départ des points dans le plan, et on
cherche à organiser ces points, en l'occurrence à trouver
le plus petit polygone qui contienne tous les points, et
soit convexe.
4 La complexité des algorithmes récursives
Géométrie algorithmique

5. Géométrie algorithmique
Historique :
 Vers les 70s: Premiers algorithmes pour résoudre les
problèmes géométriques.
 1976: Première thèse de doctorat en géométrie
algorithmique (Michael Shamos)
 1985: First Annual ACM Symposium on Computational
Geometry.
 1996: CGAL: 1ère implémentation des algorithmes
efficaces.
 1997: Le premier « handbook on computational
geometry » voit le jour (le second en 2000). [5]
La complexité des algorithmes récursives
Géométrie algorithmique
5

6. Enveloppe convexe
 L'enveloppe convexe (convex hull)
d'un ensemble S est le plus petit
ensemble CH(S) convexe,
contenant S.
 C'est aussi l'intersection de tous
les ensembles convexes contenant
S.
 Un ensemble S est convexe si pour
toute paire de points a, b Є S, le
segment ab Ϲ S.
X
✔
6 La complexité des algorithmes récursives
Géométrie algorithmique

7. Enveloppe convexe
 Soit P un ensemble de n
points du plan.
 On souhaite calculer
l'enveloppe convexe de
cet ensemble.
 C'est le polygone (fermé)
dont les sommets
appartiennent à P et qui
contient tous les points
de P.
7 La complexité des algorithmes récursives
Géométrie algorithmique

8. Enveloppe convexe
 Il peut être utilisée dans plusieurs cas.
 Exemple: si on a une antenne radio qui doit couvrir un
certain nombre de points, on va chercher la meilleure
place pour positionner cette antenne.
 Cela revient à trouver la plus petite ellipse contenant
les points. Comme cette ellipse est convexe, il est clair
que seuls les points de l'enveloppe convexe vont jouer
un rôle.
8 La complexité des algorithmes récursives
Géométrie algorithmique

9. Algorithmes…
 Pour parvenir au résultat recherché, il faut maintenant
expliquer à la machine la recette.
 l'algorithme.
 Plusieurs algorithmes et techniques s’interviennent…
9
Entrée = ensemble de points P
p1 , p2 , p3 , p4 , p5 , p6 , p7 , p8 ,
p9 , p10 , p11
Sortie = enveloppe convexe CH(P)
p7 , p2 , p3 , p8 , p6 , p10
La complexité des algorithmes récursives
Géométrie algorithmique

10. Diviser pour régner (Divide-and-
conquer)
 Idée:
 Diviser l’ensemble des éléments en deux groupes.
 Déterminer pour chaque ensemble l’enveloppe convexe
selon une méthode récursive.
 Fusionner les deux enveloppes.
 Fusion de l’enveloppe:
 Trouver les tangentes reliant les enveloppes
10 La complexité des algorithmes récursives
Géométrie algorithmique

11. Diviser pour régner (Divide-and-
conquer)
6 2 1 7 0 4 5 3
6 2 1 7 0 4 5 3
11
6 2 1 7 0 4 5 3
6 2 1 7 0 4 5 3
N=8
N=4
N=2
N=1
La complexité des algorithmes récursives
Géométrie algorithmique

12. Diviser pour régner (Divide-and-
conquer)
0 1 2 3 4 5 6 7
1 2 6 7 0 3 4 5
2 6 1 7 0 4 3 5
12
6 2 1 7 0 4 5 3
6 2 1 7 0 4 5 3
La complexité des algorithmes récursives
Géométrie algorithmique

13. Diviser pour régner (Divide-and-
conquer)
 Le problème se divise en
deux sous-problèmes de
taille approximative n/2.
 2 T(n/2)
 La division et la fusion sont
effectués en un temps D(n)
et C(n).
 O (n).
 Par conséquent, le temps
d'exécution de l'algorithme
est en  O(n log n).
13 La complexité des algorithmes récursives
Géométrie algorithmique

14. Recherche Binaire (Binary
search)
 Elle peut être vue comme une divide-and-conquer
méthode.
 Chaque itération élimine la moitié des possibilités
restantes.
 Cela rend les recherches binaires très efficace.
 Elle nécessite une collecte sélective.
 Cela signifie la collecte doit être triés avant de chercher.
14 La complexité des algorithmes récursives
Géométrie algorithmique

15. Recherche Binaire (Binary
search)
Chercher l’élément x=14
15
✔
111 222 555 777 888 111111 111222 111444 111777
La complexité des algorithmes récursives
Géométrie algorithmique

16. Recherche Binaire (Binary
search)
Principe dichotomie :
 À chaque étape d’itération,
l’intervalle de recherche doit
être divisé par deux.
 T(n/2)
 Le test est en  O(1).
 Le temps d’exécution est en
 O(log n).
16 La complexité des algorithmes récursives
Géométrie algorithmique

17. Autres…
 Brute Force
 Algorithme de la ficelle (Jarvis)
 Gift Wrapping
 Quickhull
 …
17 La complexité des algorithmes récursives
Géométrie algorithmique

18. Théorèmes générales
 n : la taille du problème
 a : le nombre des sous
problèmes dans la
récursivité.
 n/b : la taille de chaque
sous-problème.
 f : le coût des traitement
que l'algorithme fait en
dehors des appels
récursifs.
 Si a≥1 , b>1 alors
T(n) = aT(n/b) + f(n)
18 La complexité des algorithmes récursives
Géométrie algorithmique

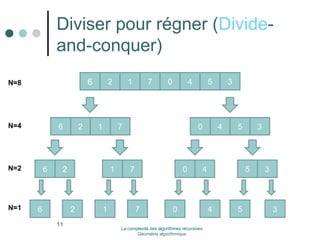
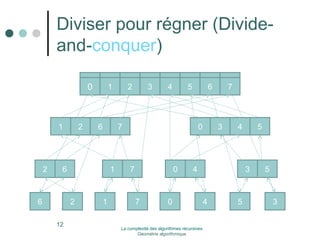
19. Théorèmes générales
(Démonstration: voir [1])
La complexité des algorithmes récursives
Géométrie algorithmique
19

20. Théorèmes générales
La complexité des algorithmes récursives
Géométrie algorithmique
20

21. Conclusion
 La géométrie algorithmique est un domaine vague
contenant plusieurs algorithmes qui traitent des
concepts géométriques.
 Parmi ces algorithmes, il y’a ceux qui traitent l’enveloppe
convexe.
 Ils permettent d’organiser des points/ des éléments dans
un plan.
 Des techniques sont utilisées par ces algorithmes.
 Nous avons cité le « divide-and-conquer » et le « binary
search ».
 Pour calculer la complexité des algorithmes, il y’a des
théorèmes qui peuvent s’appliquer dans le domaine de la
géométrie algorithmique.
21 La complexité des algorithmes récursives
Géométrie algorithmique

22. Merci pour votre attention

22 La complexité des algorithmes récursives
Géométrie algorithmique

23. Bibliographie
[1]: Complexity of recursive algorithms, Computational Geometry, Vera
Sacristan
[2]: Computational Geometry: from Theory to Applications (2013/14) -
Luca Castelli Aleardi et Steve Oudot
[3]: Computational Geometry: Algorithms and Applications, Third Edition
(March 2008), Mark de Berg, Otfried Cheong, Marc van Kreveld, Mark
Overmars, published by Springer-Verlag
[4]: https://interstices.info/algorithme-geometrique
[5]: Les enveloppes convexes en géométrie algorithmique, Achraf Othman
[6]: Les enveloppes convexes en géométrie algorithmique, Achraf Othman
[7]: Computational Geometry:Convex Hulls
[8]: http://www.youtube.com/watch?v=NQMUQpmurFI
[9]: Master Theorem: Practice Problems and Solutions
[10]: Un joli algorithme géométrique et ses vilains problèmes numériques,
Olivier Devillers, 2006
23 La complexité des algorithmes récursives
Géométrie algorithmique