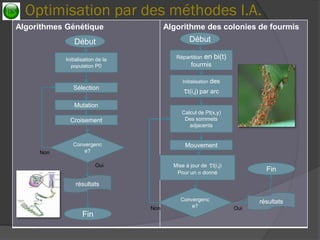
Le document traite des fondements et méthodologies de la recherche opérationnelle (RO), qui vise à optimiser le fonctionnement des systèmes par des approches scientifiques. Il couvre différents domaines tels que la théorie des systèmes, des graphes, l'optimisation des systèmes linéaires et non-linéaires, ainsi que l'utilisation des algorithmes d'intelligence artificielle pour l'optimisation. En conclusion, il souligne l'importance d'une interaction efficace avec les systèmes environnants pour améliorer les performances et réduire les pertes.

1. Cours
http://www.univ-bechar.dz/tamali
Pr. TAMALI Mohammed
mtamali@gmail.com

2. Plan
1.Généralités & positionnement de l’Opt./RO
2.Théorie des systèmes
3.Théorie des graphes
4.Outils de l’optimisation
5.Optimisation des systèmes linéaires
6.Optimisation des systèmes non-linéaires
7.Optimisation par méthodes I.A.
8.Sensibilité des systèmes
9.Conclusion

3. Généralité &Positionnement Opt./RO
La recherche opérationnelle (RO) vise à l'amélioration du fonctionnement des organisations de systèmes par l'application de l'approche scientifique. Reposant sur l'utilisation de méthodes scientifiques, de techniques spécialisées et des ordinateurs, la RO permet d'obtenir une évaluation quantitative des politiques, stratégies et actions possibles dans le cours des opérations d'une organisation ou d'un système. Une optimisation présume Une fonctionnelle F(X) Des variables X Des contraintes G(X) Des liaisons H(X) Un domaine de définition  Une frontière  Du courage, de la patience et une bonne méthode

4. Théorie des systèmes
()
()
(S)
{F (X)}opt
G(X)b1
H(X)=b2
Cond(X)
La théorie des systèmes introduite pour la première fois en 1968 par Bertalanffy L. Von, dans son livre "General System Theory: Foundations, Development, Applications".
Bertalanffy, décrivait dés lors que l'univers qui nous entoure n'est que composition d'une infinité d'entités fonctionnelles pouvant être appelées chacune SYSTEME.
De cette théorie en émerge d’autres, la cybernétique, la systhèmique

5. Théorie des graphes
La théorie des graphes, Les graphes modélisent de nombreuses situations concrètes où interviennent des objets en interaction. Les réseaux d'ordinateurs, les éléments d’un moteur. Les graphes permettent de manipuler plus facilement des objets et leurs relations avec une représentation graphique naturelle. Comment minimiser ou plutôt optimiser la longueur totale des interconnexions fonctionnelles dans un circuit? Comment décider, étant donnée une situation caractérisée par un nombre d'hypothèses? La théorie des graphes est aussi importante dans beaucoup de domaines scientifiques, on cite :
•Le problème du transport
•L'optimisation
•La robotique
•la théorie de l'information
•Optimisation de la coordination des composantes d’un système
Définitions : Sommet, arc,
Multi-Graphe, Matrices incidence A
Matrice d’adjacence M, Arbre
Connexité.

6. Outils de l’optimisation
Les outils de l’optimisation se regroupe généralement dans la méthodologie adoptée pour mener à bien une tâche éventuelle.
L’OBSERVATION : soumettre le système aux sens de la
Perception naturels ou artificiels avec une totale
objectivité.
LA FORMALISATION : fixer les observations par une symbolisation appropriée {ei, xi}
LA MODELISATION : Composer les symboles et les relations en un équivalent
LA SIMULATION : faire travailler l’équivalent et observer le fait qu’il reflète les même manifestions que le système réel.
L’OPTIMISATION : Déterminer, suivant une méthodologie, le
Meilleur état du système répondant au compromis
coût/Performance.
LA PRISE DE DECISION : Adopter, vus les exigences du système et
De ceux qui lui sont adjacents/en interaction, une position par
Rapport aux résultats de l’optimisation.

7. Optimisation des systèmes linéaires
Soit une usine de fabrication de pièces mécanique. Trois types de pièces sont dans la gamme de pièces produites et ceci avec 80 machines. Considéré dans la durée d’un mois, l’usine est tenu de présenter une stratégie de production dans les conditions suivantes. Une pièce du type I est exécutée en 5 heures, une du type II est faite en 1.30 heures alors que celle du dernier type en 3 heures. Les débouchés au marché de chaque type prit séparément sont de 3000, 1500 et 2000 unités respectivement. Les bénéfices par unité vendue sont à 8, 5 et 3 DA pour les types I, II et III. Déterminer une stratégie de production
•Si les durée d’exécution augmentent
•Si les limites de vente au marché diminuent
•Si les imposition changent

8. Optimisation des systèmes non-linéaires
Soit (S) un système non linéaire dont F(X) est le modèle mathématique le représentant
Le problème s’écrit :
On peut toujours se contenter de XoptX* (où |X*-Xopt|;  petit
Si m est le nombre de contraintes et les liaisons.
* 21)( )( )( )( XestSdesolutionLaXbXHbXGbXFnopt             mjpourXLnipourxXLsontsoptimalitédconditionslesdoncXHXGXFXLjiT..10),( ..10),( :' )()(.)(),(           

9. Optimisation par des méthodes I.A.
Algorithmes Génétique
Algorithme des colonies de fourmis
Début
Initialisation de la population P0
Sélection
Mutation
Croisement
Convergence?
Non
Oui
résultats
Fin
Début
Répartition en bi(t) fourmis
Initialisation des
t(i,j) par arc
Calcul de Pt(x,y)
Des sommets adjacents
Mouvement
Convergence?
résultats
Fin
Mise à jour de t(i,j)
Pour un  donné
Oui
Non

10. Sensibilité des systèmes
La sensibilité de (S) est égale à la dérivée de fonction le régissant par rapport à ses variable. Elle indique clairement que n’import quelle variation sur les variables pourrait induire un éloignement par rapport de la valeur optimale de l’état du système.
De même, il est possible de voire comment F est sensible à une variable double (dire multiple) d’un couple de variable xi, xj (dire xi, …,xk).
nkavecxXFk..1; )(    njiavecxxXFji..1,; )(2   

11. Conclusion
Il est bien clair que la meilleur position qu’un système peut prendre est celle qui représente l’état suivant :
1.Une interaction homogène avec les systèmes adjacents
2.Un consommation minimale de l’énergie
3.Une fiabilité meilleure
4.Des pertes minimes