Le document présente le laboratoire d'énergétiques en zones arides de l'université de Béchar, axé sur la modélisation et la simulation pour résoudre des problématiques liées aux zones arides. Il aborde des concepts d'optimisation et de théorie des systèmes, ainsi que des applications en modélisation, programmation et théorie des graphes, soulignant leur importance dans divers domaines scientifiques. Le laboratoire vise à développer des codes informatiques accessibles en ligne pour améliorer la gestion et le suivi des processus énergétiques et environnementaux.





![Equation de croissance
Equation de croissance
Théorie des systèmes
Théorie des systèmes
La théorie des systèmes est la science de l’étude
transdisciplinaire de l’organisation abstraite des phénomènes,
indépendamment de leur substance, leur type ou leur échelle
spatiale/temporelle de l’existence. Elle étudie à la fois, les
principes communs à toutes les entités complexes, et les
modèles (généralement mathématiques) qui peuvent être
utilisés pour les décrire.
Dans sa plus simple expression, l’équation différentielle,
appelée équation de croissance de Ludwig Von Bertalanffy,
où est postulé que la taille (L) par rapport au temps (t) :
L’(t) = k.(L∞
- L(t))
Où k est le taux de croissance individuel et L∞
la taille
individuelle maximum.
Selon Bertalanffy, tout est SYSTÈME par défaut.
Et tout contribue à la tenue de son environnement système
Et y est influencé.
La théorie des systèmes est la science de l’étude
transdisciplinaire de l’organisation abstraite des phénomènes,
indépendamment de leur substance, leur type ou leur échelle
spatiale/temporelle de l’existence. Elle étudie à la fois, les
principes communs à toutes les entités complexes, et les
modèles (généralement mathématiques) qui peuvent être
utilisés pour les décrire.
Dans sa plus simple expression, l’équation différentielle,
appelée équation de croissance de Ludwig Von Bertalanffy,
où est postulé que la taille (L) par rapport au temps (t) :
L’(t) = k.(L∞
- L(t))
Où k est le taux de croissance individuel et L∞
la taille
individuelle maximum.
Selon Bertalanffy, tout est SYSTÈME par défaut.
Et tout contribue à la tenue de son environnement système
Et y est influencé.
Autrichien [1901-1972],
Biologie, Écologie, Médecine,
Psychologie,
Théorie générale des systèmes
Autrichien [1901-1972],
Biologie, Écologie, Médecine,
Psychologie,
Théorie générale des systèmes
6
6](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-6-320.jpg)






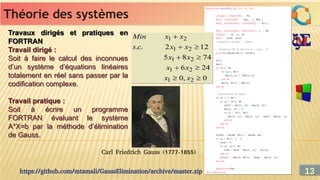
![Théorie des graphes
Théorie des graphes
On fait généralement remonter la naissance de la Théorie des Graphes au célèbre
problème des ponts de Königsberg (aujourd'hui Kaliningrad) qui passionnait la
bourgeoisie prussienne du XVIIIème siècle : La Ville de Königsberg, sur la Pregel, était
pourvue de 7 ponts et la question était de savoir si l'on pouvait imaginer une
promenade dans la ville qui emprunterait chacun des 7 ponts une fois et une seule
pour revenir à son point de départ.
La théorie des graphes s’est alors développée et intégrée dans diverses
disciplines telles que la chimie, la biologie, les sciences sociales et sans
oublier les réseaux d’ordinateurs et de télécommunication. Depuis le
début du XXe siècle, elle constitue une branche à part entière des
mathématiques, grâce aux travaux de König, Menger, Cayley puis de
Berge et d’Erdös [1].
De manière générale, un graphe permet de représenter la structure, les
connexions d’un ensemble complexe dit ‘système’ (S) en exprimant les
relations entre ses éléments tel que les réseaux de communication, les
réseaux routiers, interaction de diverses espèces animales, circuits
électriques, en programmation et le plus intéressant son application aux
sciences de l’Internet.
On fait généralement remonter la naissance de la Théorie des Graphes au célèbre
problème des ponts de Königsberg (aujourd'hui Kaliningrad) qui passionnait la
bourgeoisie prussienne du XVIIIème siècle : La Ville de Königsberg, sur la Pregel, était
pourvue de 7 ponts et la question était de savoir si l'on pouvait imaginer une
promenade dans la ville qui emprunterait chacun des 7 ponts une fois et une seule
pour revenir à son point de départ.
La théorie des graphes s’est alors développée et intégrée dans diverses
disciplines telles que la chimie, la biologie, les sciences sociales et sans
oublier les réseaux d’ordinateurs et de télécommunication. Depuis le
début du XXe siècle, elle constitue une branche à part entière des
mathématiques, grâce aux travaux de König, Menger, Cayley puis de
Berge et d’Erdös [1].
De manière générale, un graphe permet de représenter la structure, les
connexions d’un ensemble complexe dit ‘système’ (S) en exprimant les
relations entre ses éléments tel que les réseaux de communication, les
réseaux routiers, interaction de diverses espèces animales, circuits
électriques, en programmation et le plus intéressant son application aux
sciences de l’Internet.
14
14](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-14-320.jpg)
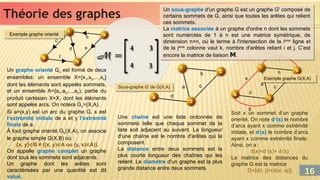
![Théorie des graphes
Théorie des graphes
Les graphes constituent donc une
méthode de pensée qui permet de
modéliser une grande variété de
problèmes en se ramenant à l’étude de
sommets et d’arcs. Les derniers
travaux en théorie des graphes sont
souvent effectués par des
informaticiens, du fait de l’importance
que revêt l’aspect algorithmique.
Les graphes constituent donc une
méthode de pensée qui permet de
modéliser une grande variété de
problèmes en se ramenant à l’étude de
sommets et d’arcs. Les derniers
travaux en théorie des graphes sont
souvent effectués par des
informaticiens, du fait de l’importance
que revêt l’aspect algorithmique.
Un graphe simple noté G est un couple
formé de deux ensembles liés par une
application mathématique. L’un d’eux est
l’ensemble X={x1,x2,...,xn} dont les
éléments sont appelés ‘sommets’, l’autre
est l’ensemble A={a1,a2,...,am}, partie de
l’ensemble P2
(X) des parties à deux
éléments (couple de sommets) de X, dont
les éléments sont appelé ‘les arêtes’. On
notera cette relation G=(X,A).
Lorsque a={x,y}A, on dit que a est l’arête
de G d’extrémités x et y, ou que a joint x et
y, ou que a passe par x et y. Les sommets
x et y sont dits adjacents dans G.
Un graphe simple noté G est un couple
formé de deux ensembles liés par une
application mathématique. L’un d’eux est
l’ensemble X={x1,x2,...,xn} dont les
éléments sont appelés ‘sommets’, l’autre
est l’ensemble A={a1,a2,...,am}, partie de
l’ensemble P2
(X) des parties à deux
éléments (couple de sommets) de X, dont
les éléments sont appelé ‘les arêtes’. On
notera cette relation G=(X,A).
Lorsque a={x,y}A, on dit que a est l’arête
de G d’extrémités x et y, ou que a joint x et
y, ou que a passe par x et y. Les sommets
x et y sont dits adjacents dans G.
Un multi-graphe G = (X, A, f) est déterminé par:
• L’ensemble X des sommets
• L’ensemble A, cette fois abstrait
• L’application f : A [P2
(X)]
un multi-graphe avec boucles peut comprendre des arêtes
multiples entre deux sommets donnés ainsi que des boucles
multiples en un sommet.
Un multi-graphe G = (X, A, f) est déterminé par:
• L’ensemble X des sommets
• L’ensemble A, cette fois abstrait
• L’application f : A [P2
(X)]
un multi-graphe avec boucles peut comprendre des arêtes
multiples entre deux sommets donnés ainsi que des boucles
multiples en un sommet.
Exemples de cas où le modèle graphe est recommandé
Exemples de cas où le modèle graphe est recommandé
15
15](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-15-320.jpg)



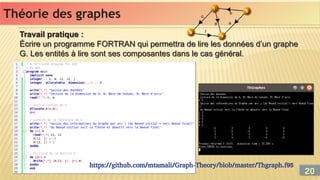




![Évaluation des performances
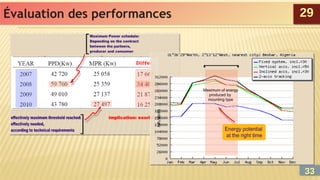
Évaluation des performances
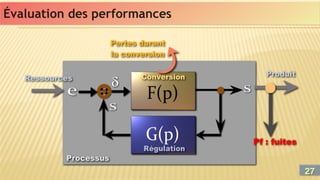
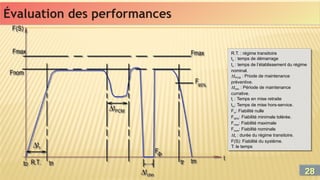
On définit la fiabilité de (S) comme étant la probabilité que le celui-ci
fonctionne correctement dans la période [0, ] et on écrit F(t≤).
De même la défaillance du système D(t≤) est définit par le
complément à 1 de la fiabilité (condition de probabilité).
D’où D(t≤)=[1 - F(t≤)].
Dans le cas de systèmes en série, leur fiabilité résultante est donnée
par :
Alors que pour le cas de système parallèles elle est donnée par :
Autrement, le système est formé par
Une configuration mixte.
On définit la fiabilité de (S) comme étant la probabilité que le celui-ci
fonctionne correctement dans la période [0, ] et on écrit F(t≤).
De même la défaillance du système D(t≤) est définit par le
complément à 1 de la fiabilité (condition de probabilité).
D’où D(t≤)=[1 - F(t≤)].
Dans le cas de systèmes en série, leur fiabilité résultante est donnée
par :
Alors que pour le cas de système parallèles elle est donnée par :
Autrement, le système est formé par
Une configuration mixte.
m
i
i t
F
t
F
1
)
(
)
(
m
i
i t
F
t
F
1
)
(
)
(
m
i
i t
F
t
F
1
))]
(
1
(
1
[
)
(
m
i
i t
F
t
F
1
))]
(
1
(
1
[
)
(
29
29](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-29-320.jpg)






![Modélisation & Simulation
Modélisation & Simulation
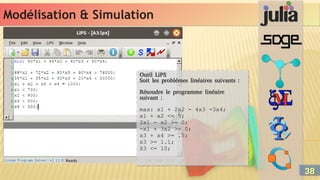
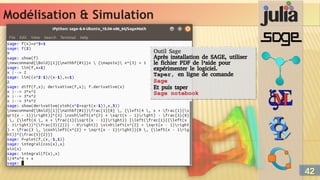
Outil Octave
Soit l’équation différentielle suivante :
>> function xdot = f (x, t)
> r = 0.25;
> k = 1.4;
> a = 1.5;
> b = 0.16;
> c = 0.9;
> d = 0.8;
> xdot(1) = r*x(1)*(1-x(1)/k)-a*x(1)*x(2)/(1+b*x(1));
> xdot(2) = c*a*x(1)*x(2)/(1+b*x(1))-d*x(2);
> endfunction
Et dont les condition initiale sont :
> x0 = [1; 2];
Le paramètre t est définit par
> t = linspace (0, 50, 200)';
La solution du problème est donnée par l’intergration
> x = lsode ("f", x0, t);
Le traçage de la fonction se fait par invocation de :
> plot (t, x)
Outil Octave
Soit l’équation différentielle suivante :
>> function xdot = f (x, t)
> r = 0.25;
> k = 1.4;
> a = 1.5;
> b = 0.16;
> c = 0.9;
> d = 0.8;
> xdot(1) = r*x(1)*(1-x(1)/k)-a*x(1)*x(2)/(1+b*x(1));
> xdot(2) = c*a*x(1)*x(2)/(1+b*x(1))-d*x(2);
> endfunction
Et dont les condition initiale sont :
> x0 = [1; 2];
Le paramètre t est définit par
> t = linspace (0, 50, 200)';
La solution du problème est donnée par l’intergration
> x = lsode ("f", x0, t);
Le traçage de la fonction se fait par invocation de :
> plot (t, x)
40
40](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-40-320.jpg)


![Système linéaire
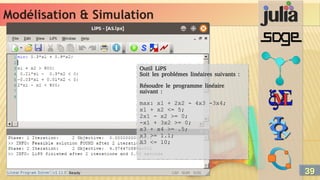
Système linéaire
Principe de proportionnalité : si s(t) est la réponse à l'entrée e(t)
alors λ*s(t) est la réponse à l'entrée λ*e(t).
Principe de superposition : si s1(t) est la réponse à l'entrée e1(t) et
s2(t) est la réponse à l'entrée e2(t) alors [s1(t) + s2(t)] est la
réponse à l'entrée [e1(t) + e2(t)].
Allure de la courbe d’un SL : pour un système linéaire, en régime
nominal (en fonctionnement normal et sans excitation
perturbatrice), la courbe s = f(e) est une droite.
Un système est continu, par opposition à un système discret,
lorsque les variations de ses composantes sont continûment
observable.
Un système est invariant (stationnaire) si ses caractéristiques
sont insensibles aux changements du temps.
selon ces faits, le système linéaire SL reflète les mêmes réactions
indépendamment du temps.
Principe de proportionnalité : si s(t) est la réponse à l'entrée e(t)
alors λ*s(t) est la réponse à l'entrée λ*e(t).
Principe de superposition : si s1(t) est la réponse à l'entrée e1(t) et
s2(t) est la réponse à l'entrée e2(t) alors [s1(t) + s2(t)] est la
réponse à l'entrée [e1(t) + e2(t)].
Allure de la courbe d’un SL : pour un système linéaire, en régime
nominal (en fonctionnement normal et sans excitation
perturbatrice), la courbe s = f(e) est une droite.
Un système est continu, par opposition à un système discret,
lorsque les variations de ses composantes sont continûment
observable.
Un système est invariant (stationnaire) si ses caractéristiques
sont insensibles aux changements du temps.
selon ces faits, le système linéaire SL reflète les mêmes réactions
indépendamment du temps.
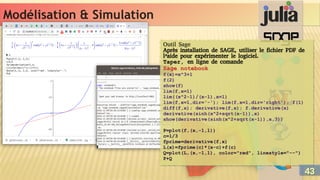
Un système d’équations linéaires SEL (ζ) est la
composition faite de n équations linéaires :
a11x1 + a12x2 + … = k1
a21x1 + a22x2 + … = k2
….
an1x1 + an2x2 + … = kn
où x1, x2, … xp sont les p inconnues du système alors que
k1, k2, … kn sont les n termes du second membre ou
constantes et les aij sont les n*p coefficients du système
ou multiplicateur des variable xi.
Géométriquement (ζ), les n équations représentent les n
droites en intersection dans un référentiel Rn
.
Un système d’équations linéaires SEL (ζ) est la
composition faite de n équations linéaires :
a11x1 + a12x2 + … = k1
a21x1 + a22x2 + … = k2
….
an1x1 + an2x2 + … = kn
où x1, x2, … xp sont les p inconnues du système alors que
k1, k2, … kn sont les n termes du second membre ou
constantes et les aij sont les n*p coefficients du système
ou multiplicateur des variable xi.
Géométriquement (ζ), les n équations représentent les n
droites en intersection dans un référentiel Rn
.
Les systèmes non linéaires sont plus difficiles à étudier
que les systèmes linéaires. Néanmoins, en linéarisant,
autour d'un point de considération finie (équilibre
fonctionnel), on obtient un système linéaire qui correspond
au système non linéaire.
Cette approche a atteint sa maturité dans le livre de H.W.
Bode (1905-1982) à la fin de la II guerre mondiale. Les
travaux de R.E.Bellman (1920-1984), L.S.Pontryagin
(1908-1988) et al et surtout de R.Kalman (1930) ont
conduit nombre d'automaticiens à privilégier la
représentation d‘espace d’état à partir des années 1960.
Un système est linéaire s’il se comporte linéairement par
rapport à ses composantes intrinsèques.
Les systèmes non linéaires sont plus difficiles à étudier
que les systèmes linéaires. Néanmoins, en linéarisant,
autour d'un point de considération finie (équilibre
fonctionnel), on obtient un système linéaire qui correspond
au système non linéaire.
Cette approche a atteint sa maturité dans le livre de H.W.
Bode (1905-1982) à la fin de la II guerre mondiale. Les
travaux de R.E.Bellman (1920-1984), L.S.Pontryagin
(1908-1988) et al et surtout de R.Kalman (1930) ont
conduit nombre d'automaticiens à privilégier la
représentation d‘espace d’état à partir des années 1960.
Un système est linéaire s’il se comporte linéairement par
rapport à ses composantes intrinsèques.
Bellman
Bellman
Kalman
Kalman
Pontryagin
Pontryagin
Bode
Bode 48
48](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-48-320.jpg)


![Système linéaire
Système linéaire
Méthode de Simplexe
Soit à optimiser, par la méthode Simplexe la fonction objectif Z = CT
.X sous les contraintes
1(X) ≤ b1, 2(X) = b2 et 3(X) ≥ b3
X≥0 (condition économique), b1 b2 b3 = b : vecteur second membre
Les i sont les fonction contraintes d’inégalités i [1,m].
Une écriture condensée de la forme (PL) :
Z = CT
.X
s.c.
(X) ≤ b
X≥0
Est toujours possible.
Solution réalisable
Par addition / soustraction de quantités si à chaque équation contrainte, nous obtenons la forme
aisée suivante (forme PL1) :
Z = CT
.X
s.c.
’(X, si) = ’(X’) = b avec X’=X si.
X≥0
Si nous considérons N, l’ensemble des indices des variables de X, on peut toujours choisir m
variables parmi n. Ces dernières formerons la solution SUPPOSEE du problème.
N = {1, 2, 3, …, n}
Avec les m indices parmi n, nous construirons un ensemble β dit BASE REALISABLE.
Méthode de Simplexe
Soit à optimiser, par la méthode Simplexe la fonction objectif Z = CT
.X sous les contraintes
1(X) ≤ b1, 2(X) = b2 et 3(X) ≥ b3
X≥0 (condition économique), b1 b2 b3 = b : vecteur second membre
Les i sont les fonction contraintes d’inégalités i [1,m].
Une écriture condensée de la forme (PL) :
Z = CT
.X
s.c.
(X) ≤ b
X≥0
Est toujours possible.
Solution réalisable
Par addition / soustraction de quantités si à chaque équation contrainte, nous obtenons la forme
aisée suivante (forme PL1) :
Z = CT
.X
s.c.
’(X, si) = ’(X’) = b avec X’=X si.
X≥0
Si nous considérons N, l’ensemble des indices des variables de X, on peut toujours choisir m
variables parmi n. Ces dernières formerons la solution SUPPOSEE du problème.
N = {1, 2, 3, …, n}
Avec les m indices parmi n, nous construirons un ensemble β dit BASE REALISABLE.
Modélisation graphique du SL
Modélisation graphique du SL
51
51](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-51-320.jpg)




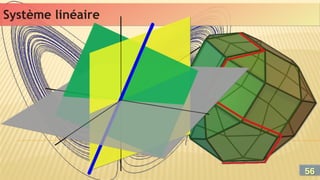

![Système non linéaire
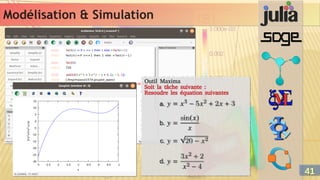
Système non linéaire
Principe de proportionnalité : si s(t) est la réponse à l'entrée
e(t) alors *s(t) est la réponse à l'entrée *e(t).
λ λ
Principe de superposition : si s1(t) est la réponse à l'entrée
e1(t) et s2(t) est la réponse à l'entrée e2(t) alors [s1(t) + s2(t)]
est la réponse à l'entrée [e1(t) + e2(t)].
Allure de la courbe d’un SNL : pour un système NON
linéaire, en régime nominal (en fonctionnement normal et
sans excitation perturbatrice), la courbe s = f(e) n’est pas
une droite. Un système SNL est continu, par opposition à un
SNL dit discret, lorsque les variations de ses composantes
sont continûment observable dans le cadre de son domaine
de définition δ.
Un système est invariant (stationnaire) si ses caractéristiques
sont insensibles aux changements du temps.
selon ces faits, le système linéaire SL reflète les mêmes
réactions indépendamment du temps.
Principe de proportionnalité : si s(t) est la réponse à l'entrée
e(t) alors *s(t) est la réponse à l'entrée *e(t).
λ λ
Principe de superposition : si s1(t) est la réponse à l'entrée
e1(t) et s2(t) est la réponse à l'entrée e2(t) alors [s1(t) + s2(t)]
est la réponse à l'entrée [e1(t) + e2(t)].
Allure de la courbe d’un SNL : pour un système NON
linéaire, en régime nominal (en fonctionnement normal et
sans excitation perturbatrice), la courbe s = f(e) n’est pas
une droite. Un système SNL est continu, par opposition à un
SNL dit discret, lorsque les variations de ses composantes
sont continûment observable dans le cadre de son domaine
de définition δ.
Un système est invariant (stationnaire) si ses caractéristiques
sont insensibles aux changements du temps.
selon ces faits, le système linéaire SL reflète les mêmes
réactions indépendamment du temps.
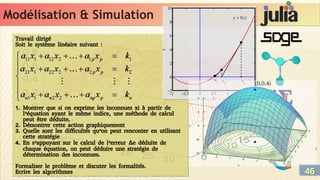
Un système d’équations non linéaires SENL (ζ) est la composition
faite de m équations non-linéaires :
f1(X) = 1(X)
f2(X) = 2(X)
….
fm(X) = m(X)
où X={x1, x2, … xp} sont les p inconnues du système alors que 1,
2, … n sont les m fonctions du second membre, elles même
dépendantes de X.
Géométriquement, les m équations représentent les m courbes
(α, β, …) en intersection dans un référentiel Rn
.
Un système d’équations non linéaires SENL (ζ) est la composition
faite de m équations non-linéaires :
f1(X) = 1(X)
f2(X) = 2(X)
….
fm(X) = m(X)
où X={x1, x2, … xp} sont les p inconnues du système alors que 1,
2, … n sont les m fonctions du second membre, elles même
dépendantes de X.
Géométriquement, les m équations représentent les m courbes
(α, β, …) en intersection dans un référentiel Rn
.
Les systèmes non linéaires sont plus difficiles à étudier que les
systèmes linéaires. Néanmoins, en linéarisant (cas de systèmes
linéarisable) un SNL, autour d'un point A de considération finie
(situation ou état du système), on obtient un système linéaire
qui correspond à une approximation grossière du système non
linéaire d’origine.
Cette approche a atteint sa maturité dans le livre de H.W.Bode
(1905-1982) à la fin de la IIème
guerre mondiale. Les travaux de
R.E.Bellman (1920-1984), L.S.Pontryagin et al (1908-1988)
surtout de R.Kalman (1930) ont conduit nombre d'automaticiens
à privilégier la représentation d‘espace d’état à partir des
années 1960.
Un système est non linéaire s’il se comporte non linéairement
par rapport à ses composantes intrinsèques.
Les systèmes non linéaires sont plus difficiles à étudier que les
systèmes linéaires. Néanmoins, en linéarisant (cas de systèmes
linéarisable) un SNL, autour d'un point A de considération finie
(situation ou état du système), on obtient un système linéaire
qui correspond à une approximation grossière du système non
linéaire d’origine.
Cette approche a atteint sa maturité dans le livre de H.W.Bode
(1905-1982) à la fin de la IIème
guerre mondiale. Les travaux de
R.E.Bellman (1920-1984), L.S.Pontryagin et al (1908-1988)
surtout de R.Kalman (1930) ont conduit nombre d'automaticiens
à privilégier la représentation d‘espace d’état à partir des
années 1960.
Un système est non linéaire s’il se comporte non linéairement
par rapport à ses composantes intrinsèques.
Bode
Bode
Bellman
Bellman
Kalman
Kalman
Pontryagin
Pontryagin
58
58](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-58-320.jpg)

![Système non linéaire
Système non linéaire
Problème type :
Un fournisseur de service GSM veut développer une nouvelle stratégie en
faveur de ses clients de marque. Pour cela, il pensa à vérifier si les
emplacements de ses cellules (antennes et équipements afférents) sont dans les
recommandations optimales de localisation. La répartition de ses clients
dépend des localités où ceux-ci exercent leur activités. La nouvelle stratégie
consiste à favoriser le client selon un profil des activités contractées et en
cours avec le fournisseur. Pour cela, répartir les antennes d’une manière
optimale selon la distance la plus courte possible des clients en question.
Formalisation
D={dip} : Vecteurs des distances qui séparent les différents antennes ai
de l’antenne principale ap(m)
xi ,yi : coordonnées du point ai d’une antenne.
dij = ([(xj-xi)2
+(yj-yi)2
]^(1/2)) : distance d’un point i à un point j (m)
S=Σdij
2
: Somme des distances à minimiser
Conditions de couverture, zone d’ombre (conditions techniques)
Modélisation graphique
Une représentation Graphe est toujours valable, mais elle ne peut identifier
que les caractères liés à une géométrie 2D seulement. Le problème donné est
un cas de système où est demandé d’optimiser (Minimiser) les distances
séparant les antennes secondaires par rapport à l’antenne primaire.
Problème type :
Un fournisseur de service GSM veut développer une nouvelle stratégie en
faveur de ses clients de marque. Pour cela, il pensa à vérifier si les
emplacements de ses cellules (antennes et équipements afférents) sont dans les
recommandations optimales de localisation. La répartition de ses clients
dépend des localités où ceux-ci exercent leur activités. La nouvelle stratégie
consiste à favoriser le client selon un profil des activités contractées et en
cours avec le fournisseur. Pour cela, répartir les antennes d’une manière
optimale selon la distance la plus courte possible des clients en question.
Formalisation
D={dip} : Vecteurs des distances qui séparent les différents antennes ai
de l’antenne principale ap(m)
xi ,yi : coordonnées du point ai d’une antenne.
dij = ([(xj-xi)2
+(yj-yi)2
]^(1/2)) : distance d’un point i à un point j (m)
S=Σdij
2
: Somme des distances à minimiser
Conditions de couverture, zone d’ombre (conditions techniques)
Modélisation graphique
Une représentation Graphe est toujours valable, mais elle ne peut identifier
que les caractères liés à une géométrie 2D seulement. Le problème donné est
un cas de système où est demandé d’optimiser (Minimiser) les distances
séparant les antennes secondaires par rapport à l’antenne primaire.
Représentation graphique du problème de la
localisation optimale des antennes.
Représentation graphique du problème de la
localisation optimale des antennes.
Exemple d’antenne utilisées pour les GSM.
Exemple d’antenne utilisées pour les GSM.
60
60](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-60-320.jpg)
![Système non linéaire
Système non linéaire
Formalisation
Soit F={fi; i[1, m]} un système de fonctions non linéaires des n variables xk/(k[1, n]) définit dans un domaine D
résultante de l’union de p sous-domaine dj, D={dj; j[1, p]}.
On définit par :
F(X)=K un problème non linéaire (SNL) à résoudre. Si K est équivalente au vecteur 0, F est dit homogène. Si C est
l’ensemble des ci contraintes définies, chacune sur un domaine dj. F(X) peut être régit par C, dans ce cas on parle de
problème non linéaire contraint.
Dans le cas où le paramètre K est égal 0 et C est vide (C=), F(X) admet des zéros A(a0, a1, …, an) dans D.
Par la méthode de Newton-Raphson, nous admettons, qu’autour d’un point X0, F(X) est explicitée sous la forme d’un
développement de Taylor et dont la forme est :
F(X0+ΔX0) F(X0)+(1/1!).[F(X)X=Xo].X0+…+(X0)
D’où X0 est la plus bonne estimation de X* (solution exacte du problème), F(X) est dite Nabla F, Gradient du système
de fonctions fi, X0 étant l’écart entre X* et X0 et finalement (X0) représente le reste de Taylor, regroupe les
dérivées d’ordres supérieur à 1 jusqu’à .
Si l’estimation est plus justifiée, (X0) tendra vers 0, puisque les termes 1/n! tend vers 0 (pour n≥2) quant n.
De ce fait on garde seulement la partie;
F(X0+X0) F(X0)+(1/1!).[F(X)X=Xo].X0, (X0) 0
Et puisque F(X) est supposée égale à 0, nous aurons
F(X0)+(1/1!).[F(X)X=Xo].X0 0 [F(X)X=Xo].X0 - F(X0)
Si on note (F(X)X=Xo)=J(X0) on a J(X0).X0 - F(X0) d’où X0 - [J(X0)]-1
.F(X0) et X = X0+X0.
Formalisation
Soit F={fi; i[1, m]} un système de fonctions non linéaires des n variables xk/(k[1, n]) définit dans un domaine D
résultante de l’union de p sous-domaine dj, D={dj; j[1, p]}.
On définit par :
F(X)=K un problème non linéaire (SNL) à résoudre. Si K est équivalente au vecteur 0, F est dit homogène. Si C est
l’ensemble des ci contraintes définies, chacune sur un domaine dj. F(X) peut être régit par C, dans ce cas on parle de
problème non linéaire contraint.
Dans le cas où le paramètre K est égal 0 et C est vide (C=), F(X) admet des zéros A(a0, a1, …, an) dans D.
Par la méthode de Newton-Raphson, nous admettons, qu’autour d’un point X0, F(X) est explicitée sous la forme d’un
développement de Taylor et dont la forme est :
F(X0+ΔX0) F(X0)+(1/1!).[F(X)X=Xo].X0+…+(X0)
D’où X0 est la plus bonne estimation de X* (solution exacte du problème), F(X) est dite Nabla F, Gradient du système
de fonctions fi, X0 étant l’écart entre X* et X0 et finalement (X0) représente le reste de Taylor, regroupe les
dérivées d’ordres supérieur à 1 jusqu’à .
Si l’estimation est plus justifiée, (X0) tendra vers 0, puisque les termes 1/n! tend vers 0 (pour n≥2) quant n.
De ce fait on garde seulement la partie;
F(X0+X0) F(X0)+(1/1!).[F(X)X=Xo].X0, (X0) 0
Et puisque F(X) est supposée égale à 0, nous aurons
F(X0)+(1/1!).[F(X)X=Xo].X0 0 [F(X)X=Xo].X0 - F(X0)
Si on note (F(X)X=Xo)=J(X0) on a J(X0).X0 - F(X0) d’où X0 - [J(X0)]-1
.F(X0) et X = X0+X0.
61
61](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-61-320.jpg)
![Système non linéaire
Système non linéaire
Formalisation
Pour un système F(X)=f(x)=0 (Cas de système à une fonction à une variable), nous avons :
f(x) = 0 f(x) = f(x0 + h) ≈ f(x0) + (f(x))’
(x0) .h, avec h=(x-x0).
x ≈ x0 + h ≈ x0 + f(x0)/(f(x0))’
Graphiquement, L’estimé initial est pris comme première
approximation de la solution, alors, par récurrence h est
recalculer de manière à corriger (par une quantité h f(x0)/(f(x0))’)
pour un sens de déplacement pour ainsi atteindre la solution.
De manière générale, nous calculerons J(X0) dite matrice
Jacobéenne du système.
X = X0 + X0 = X0 + (- [J(X0)]-1
.F(X0)])
La formule de récurence donne les estimés successifs;
Xk+1 = Xk + Xk = Xk + (- [J(Xk)]-1
.F(Xk)])
Le calcul est arrêté si et seulement si Xk tend vers zéro ou est
assimilable à une petite valeur 1 en valeur absolue (|Xk| 1).
ou encore (|Xk / Xk+1| 2). Ces deux conditions sont dites CONDITIONS D’ARRET, et le déterminant de
de J est Jacobéen (|J(X)|).
Formalisation
Pour un système F(X)=f(x)=0 (Cas de système à une fonction à une variable), nous avons :
f(x) = 0 f(x) = f(x0 + h) ≈ f(x0) + (f(x))’
(x0) .h, avec h=(x-x0).
x ≈ x0 + h ≈ x0 + f(x0)/(f(x0))’
Graphiquement, L’estimé initial est pris comme première
approximation de la solution, alors, par récurrence h est
recalculer de manière à corriger (par une quantité h f(x0)/(f(x0))’)
pour un sens de déplacement pour ainsi atteindre la solution.
De manière générale, nous calculerons J(X0) dite matrice
Jacobéenne du système.
X = X0 + X0 = X0 + (- [J(X0)]-1
.F(X0)])
La formule de récurence donne les estimés successifs;
Xk+1 = Xk + Xk = Xk + (- [J(Xk)]-1
.F(Xk)])
Le calcul est arrêté si et seulement si Xk tend vers zéro ou est
assimilable à une petite valeur 1 en valeur absolue (|Xk| 1).
ou encore (|Xk / Xk+1| 2). Ces deux conditions sont dites CONDITIONS D’ARRET, et le déterminant de
de J est Jacobéen (|J(X)|).
62
62](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-62-320.jpg)
![Système non linéaire
Système non linéaire
L’algorithme NR est donné par :
Demander X0,
1. Mettre k=0
2. Evaluer Xk+1 (à la précision désirée)
3. Si (f ’(Xk) = 0) alors Terminer
4. Répéter
a) Xk=Xk+1
b) Xk+1 = Xk + (- [J(Xk)]-1
.F(Xk)])
5. Tant que Xk≥
6. Afficher Xk+1
La méthode NR est l’une des méthode les plus simple à implémenter, très simple d’utilisation et efficace
numériquement. Beaucoup de variantes existent (Fletcher-Powell, Bellman, …)
L’algorithme NR est donné par :
Demander X0,
1. Mettre k=0
2. Evaluer Xk+1 (à la précision désirée)
3. Si (f ’(Xk) = 0) alors Terminer
4. Répéter
a) Xk=Xk+1
b) Xk+1 = Xk + (- [J(Xk)]-1
.F(Xk)])
5. Tant que Xk≥
6. Afficher Xk+1
La méthode NR est l’une des méthode les plus simple à implémenter, très simple d’utilisation et efficace
numériquement. Beaucoup de variantes existent (Fletcher-Powell, Bellman, …)
Isaac NEWTON
(1642 −1727)
Isaac NEWTON
(1642 −1727)
Joseph Raphson
(1648-1715)
Joseph Raphson
(1648-1715) 63
63](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-63-320.jpg)
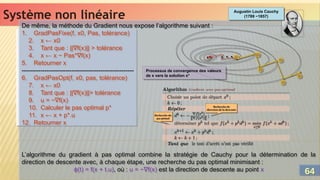
![Système non linéaire
Système non linéaire
Formalisation
Une autre stratégie consiste à réécrire le système (cas de système contraint) sous la forme :
L(X, ) = fi(X) + j.gj(X), où j est appelé multiplicateur de Lagrange
L(X, ) est la fonction de Lagrange correspondante au système à étudier.
Résoudre :
F(X) sous les contraintes gj(X) équivaut à la résolution de la fonction
de Lagrange L pour les mêmes raisons.
Les condition d’optimalité pour L sont vérifiées si :
L/xi = 0, pour i [1, n], n étant le nombre d’inconnues
L/j = 0, pour j [1, m], m étant le nombre de contraintes
Beaucoup d’autres méthodes se basent sur la démarche de Newton en se focalisant sur la détermination du
gradient de f pour explorer l’ensemble des directions de tendance vers l’optimum.
Formalisation
Une autre stratégie consiste à réécrire le système (cas de système contraint) sous la forme :
L(X, ) = fi(X) + j.gj(X), où j est appelé multiplicateur de Lagrange
L(X, ) est la fonction de Lagrange correspondante au système à étudier.
Résoudre :
F(X) sous les contraintes gj(X) équivaut à la résolution de la fonction
de Lagrange L pour les mêmes raisons.
Les condition d’optimalité pour L sont vérifiées si :
L/xi = 0, pour i [1, n], n étant le nombre d’inconnues
L/j = 0, pour j [1, m], m étant le nombre de contraintes
Beaucoup d’autres méthodes se basent sur la démarche de Newton en se focalisant sur la détermination du
gradient de f pour explorer l’ensemble des directions de tendance vers l’optimum.
Joseph-Louis Lagrange
(1739-1813)
Joseph-Louis Lagrange
(1739-1813)
65
65](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-65-320.jpg)



![Système non linéaire
Système non linéaire
69
69
S=∑
i=1
n
ei
2
=∑
i=1
n
[ yi− yi]²
S=∑
i=1
n
ei
2
=∑
i=1
n
[ yi− yi]²
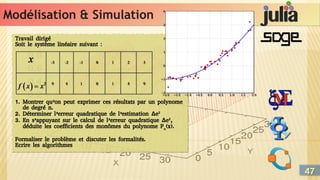
S est donc à minimiser, on cherche la plus petite
valeur de S tel que les écarts entre y et y soient
aussi petits que possible.
Yi = P2(x) = a0
+a1
*x+a2
*x2
pour que S soit
minimale il faut que :
Si on définit le facteur rxy
par cov(x,y)/sx
*sy
Et sx
2
=(1/n) (x
Σ i
-x)2
et sy
2
=(1/n)Σ(yi
-y)2
cov(x,y) = (1/n) (x
Σ i
-x)(yi
-y)
On définit un coefficient de validation de
l’ajustement par R2
=rxy
*rxy
Cette quantité est d’autant grande (tend vers 1),
plus l’ajustement pratiqué est valable
S est donc à minimiser, on cherche la plus petite
valeur de S tel que les écarts entre y et y soient
aussi petits que possible.
Yi = P2(x) = a0
+a1
*x+a2
*x2
pour que S soit
minimale il faut que :
Si on définit le facteur rxy
par cov(x,y)/sx
*sy
Et sx
2
=(1/n) (x
Σ i
-x)2
et sy
2
=(1/n)Σ(yi
-y)2
cov(x,y) = (1/n) (x
Σ i
-x)(yi
-y)
On définit un coefficient de validation de
l’ajustement par R2
=rxy
*rxy
Cette quantité est d’autant grande (tend vers 1),
plus l’ajustement pratiqué est valable
δS
δa0
=0
δS
δa0
=0 δS
δa1
=0
δS
δa1
=0
δ S
δa2
=0
δ S
δa2
=0](https://image.slidesharecdn.com/chapxi-optimisation-231026222726-c3aa000b/85/Chap-XI-Optimisation-pdf-69-320.jpg)

