Le document présente l'Université de Béchar et son laboratoire d'études énergétiques en zones arides, soulignant ses équipes de recherche et les domaines d'application de la modélisation et de la simulation. Il décrit également les concepts clés liés aux systèmes, aux méthodes de résolution d'équations et les enjeux liés à l'évaluation des performances. Enfin, le texte aborde les outils logiciels utilisés pour la modélisation et simulation, ainsi que les défis des calculs numériques.

1. Version
3.0.0
Université de Béchar
Laboratoire des Études Énergétiques en Zones Arides
Équipe Modélisation & Simulation des Systèmes
Cours réalisé par : Pr. TAMALI Mohammed,
http://mtamali.wordpress.com/
Université de Béchar | FS&T
(ENERGARID Lab./SimulIA)

2. Presentation
The University of Bechar was born in 1986 as the National Institutes of Higher
Education (INES) in 1992 it becomes University Center and on January 07, 2007, it
was officially declared as a University. Since then, many Research Teams have seen
the day. In 2011, The Laboratory for Energy Systems Studies Applied to Arid Zones
was run by a group of young and well motivated researchers (7 Research teams) to
solve real problems affecting arid zones, SimulIA Team is one of them in the same
laboratory. The Workload of SimulIA concern studies and applications of modeling
and simulation of systems in Arid Areas.
Research areas:
 Energy & Environment (Modeling & Simulation)
 Application of heat in arid zones
 Energy economy.
 Mapping and development of resources in arid zones.
 SIMULIA for the task in the short term, to develop the computer code for
modeling and simulation which can be accessed online.
Website of the laboratory team: http://energarid.wordpress.com/
2

3. Généralités
Caractéristiques des systèmes & Modélisation (Définitions,
Typologie, Méthodologie)
Domaines d’application
Systèmes représentation des données
Systèmes linéaires (Méthode directe, itérative,)
Systèmes non-linéaires (Méthode variationnelle)
Interpolation & approximation (Statistique, Lissage, Extrapolation)
Intégration numérique
Equation différentielle (Méthode d’Euler, Runge-Kutta)
Conclusion
Plan
3

4. Généralités
Les mathématiques appliquées et le calcul scientifique jouent un rôle croissant
dans la conception de produits industriels; ce n’est cependant qu’un maillon
d’une longue chaîne qui mobilise des ressources intellectuelles nombreuses et
variées pour arriver à concevoir, au mieux et dans des délais impartis le produit
désiré. Le niveau de complexité des systèmes est très élevé à un niveau où toute
intégration sociale des produits résultants ne se ferait sans dégâts ni sans effets
secondaires. En contre partie, la majorité des produits technologiques sont
juste la solution immédiate de bon nombre de problèmes de la vie courante.
L'avènement de produits, de grande consommation, comme l'informatique,
l'Internet et les télécommunications, à chacun ses outils, a révolutionné les
méthodologies de travail des équipes et laboratoires de recherches. Les outils
et suites logiciels sont d’un grand secours aux travaux de modélisation et de
simulation des processus. L'informatique et les moyens de conception sont les
vecteurs qui ont provoqué une amélioration nette à la vitesse de mise en œuvre
de moyens exploitables. Les logiciels de CAO (Conception Assistée par
Ordinateur) ont joué un grand rôle dans le cours de développement de
beaucoup de procédés (Modélisation) et ont facilité la compréhension de
beaucoup phénomènes (Simulation).
4

5. Caractéristiques des systèmes & Modélisation
Modélisation
Pour la modélisation, le système étudié est appelé système primaire.
Son modèle (équivalent) est une représentation de la réalité et il est
dit système secondaire. Par définition un modèle est une
représentation simplifiée de la réalité. Le but majeur de cette
opération c’est DÉCRIRE, PRÉDIRE, EXPLIQUER & RÉAGIR.
Modélisation graphique
C’est une stratégie modélisatrice des
système utilisant le graphique comme
langage et outil de travail.
Finalité de la modélisation
• Technique : fournir des spécifications claires pour
produire, puis exploiter
• Intellectuelle : fournir au métier, une utilité dans les
structures sociétales.
Lessuites logiciels desimulation
Composition faites des deux entités, Les
SYSTÈMES d’INFORMATION (Collections
d’informations) et les MATHEMATIQUES
(Collections d’algorithmes de calcul). C’est le
moyen utilisé pour allié efficacité et
utilisabilité des études et des coûts
équivalents à une réelle expérimentation.
Les objectifs sont généralement pour des
stratégies d’aide à la décision.
Courbes d’évolution
d’un phénomène
physique
Modèle SIG d’une urbanisation
Sous QGIS (GPL)
Exemple Arduino ISP sous Fritzing (GPL)
5

6. L’objet de ce chapitre est de mettre en évidence les principales
difficultés liées à la pratique des calculs numériques sur
ordinateur. Dans beaucoup de situations, il existe des
méthodes spécifiques permettant d’accroître `a la fois
l’efficacité et la précision des calculs. Ces équations sont
souvent très complexes, et font intervenir énormément de
paramètres. Elles sont en général impossible à résoudre de
façon exacte (comme le serait une équation différentielle du
second degré par exemple, modélisant le mouvement d’un
pendule de longueur l : Le problème linéarisé pour de petits
mouvements du pendule s’écrit en terme de x. Cette dernière
équation peut, maintenant être résolue par (formule 2):
On peut alors calculer x(t) (formule 3) pour tout temps de
façon exacte (modulo les erreurs d’arrondi). Par contre on ne
connaît pas de solution exacte de l’équation plus haut.
L'analyse numérique est l'une des thématiques de la recherche
opérationnelle, des sciences de l'ingénieur et de l'informatique.
Logiciel de visualisation graphique
Paraview (GPL)
Canevas graphique
Panneau des
propriétés
Ligne du temps,
pour l’animation
Barre d’outils
Menu principal
Caractéristiques des systèmes
Formule 2 Formule 3
6

7. Besoin : insatisfaction, nécessité, exigence, manque, nécessaire, indispensable. Sentiment de privation qui porte à
désirer ce dont on croit manquer, nécessité impérieuse : exemple; Besoin de savoir, Chose considérée comme
nécessaire à l'existence.
Observation : apercevoir, percevoir, voir, considérer, surveiller, contempler
Formalisation : Action de réduire un système de connaissances à des structures formelles.
Modélisation : Établissement de modèles, notamment des modèles utilisés en automatique, en informatique, en
recherche opérationnelle et en économie.
Simulation : Représentation du comportement d'un processus physique, industriel, biologique, économique ou militaire
au moyen d'un modèle matériel dont les paramètres et les variables sont les images de ceux du processus étudié. (Les
modèles de simulation prennent le plus souvent la forme de programmes d'ordinateurs auxquels sont parfois associés
des éléments de calcul analogique.)
Optimisation : Action d'optimiser ou d'optimaliser ; fait d'être optimisé ou optimalisé. Démarche consistant à rendre
optimal le fonctionnement d'un système
Évaluation des performances : Évaluation des capacités d’interaction du système vis-à-vis d’un ensemble de données
selon dans hypothèses prédéfinies. Le système peut existé ou non. Dans le premier cas, nous demandons une
amélioration dans la première et une bonne conception pour le cas du deuxième type. Ils existent des techniques
spécifiques pour évaluer la performance des systèmes.
Prise de décision : Choisir, dans un état de compromis, quel choix à adopter. Il est judicieux de remarquer que cette
mesure est beaucoup délicate puisque le critère le plus dangereux de de telle situation, c’est de beaucoup perdre.
Fiabilité : Répondre à tous les critères de réponses à la requête émises derrière notre conception du système.
Probabilité pour qu'une pièce primaire, un dispositif ou un équipement complet soit utilisé sans défaillance pendant une
période de temps déterminée, dans des conditions opérationnelles spécifiées
Robustesse : Un système robuste doit résister bien aux causes d'agression ou d'altération, c’est encore la tolérance aux
fautes.
Compromis : Convention par laquelle les parties à un litige soumettent l'objet de celui-ci à un arbitrage, c’est aussi
l’Action qui implique des concessions réciproques.
Caractéristiques des systèmes 7

8. Domaines d’application
Les suites logiciels de modélisation et de simulation des systèmes et des
procédés sont de deux catégories vis-à-vis des droits et devoir d’utilisation.
Pour ces mêmes suites, il y a le développeur du produit, d’un côté, et
l’utilisateur final de l’autre. A chacun ses droits mais limitées selon des clauses
et les recommandations, sur base de quoi, le deux partenaires se sont mis
d’accord. Ces termes définissent ici ce qui est communément appelé
LICENCE.
Cette dernière décrit clairement les partenaires, le produits et limites de chacun
par rapport à la loi.
Il existe deux type de licence:
• Propriétaire,
• Libre d’utilisation dite encore GPL
Dans le premier type, le développeur se doit de porter assistance à ses clients
et de garantir la continuité du service. Au même moment que les clients ne
doivent, et aucun cas, porter préjudice à leur mode ou manière d’utilisation du
produit, ne pas l’utiliser qu’avec le consentement du développeur, ne pas
l’altérer par un quelconque moyen. La distribution du produit est, de ce fait
totalement interdite.
Le client est, par ailleurs, bien en état de connaissance de tout dommage qui
pourrait éventuelle lui être causé par sont utilisation du produit et pour lequel la
partie développeur, décline toute responsabilité.
Pour le deuxième type, le développeur se partage les droits/devoirs de
re/développer le produit avec son client.
Les suite GPL (General Public Licence) sont généralement des contributions
qui évoluent pour gagner du terrain. Le paquetage est distribuer avec le fichier
binaire, tous les fichiers bibliothèques et annexes en plus de la documentation.
Ces suites sont déployée et présentent
leur service selon deux mode, Localisé
(Stand Alone/Desktop) ou bien
réparties sur le Web (Web Based).
Elle peuvent avoir besoin de données
Localisé ou Distribué.
Architecture Intranet universitaire
8

9. Domaines d’application
La plupart des domaines de l’Ingénieur.
Informatique
Electronique
Thermique
Resistance des matériaux
Chimie
Avionique
Modélisation et Simulation des processus
Et même ceux dits Sciences Humaine
Statistiques
Biologie
Médecine
Chirurgie
Encore …
Sport
Art !
9

10. Domaines d’application (Evaluation des Performances.)
D’une manière générale, l’évaluation des
performances EP c’est l’ensemble de protocoles
et des procédures à envisager en vue d’une
expertise du système (S) en cours de conception
ou d’exploitation.
On cherche dans toutes les situations d’améliorer
les performance du système en question vis-à-vis
d’une exigence/demande en attente. Le système
(S) amélioré répond avec robustesse.
On distingue généralement beaucoup de secteurs
visés par cette EP, en l’occurrence la GRH,
Métiers, Entreprise, Impact associatif et bien
d’autre … 10

11. Systèmes représentation des données
La mémoire centrale est un ensemble de ’positions binaires’ nommées bits. Les bits sont
généralement regroupés en octets (8 bits) et chaque octet est repéré par son adresse. Chaque
information devra être codée sous cette forme binaire.
En informatique,
le kilo vaut 1K = 210 = 1024
le méga vaut 1M = 220 = 1048576
le giga vaut 1G = 230 = 1073741824
Les nombres entiers dont la représentation et la manipulation sont celles de l’arithmétique usuel. Il
existe un plus grand entier représenté en machine. Pour ceux à 32 bits (=4 octets) correspond à
des entiers en double précision ont pour valeur dans [−231,231−1] = [−2G, 2G−1].
Les nombres flottants qui représentent les nombres réels ou les nombres décimaux.
Les nombres réels sont représentés de façon approximative en mémoire (représentation en virgule
flottante), avec la convention standardisée de la forme m×2e, où m est la mantisse 1≤m≤2 et e
l’exposant.
Représentation en simple précision. Sur 32 bits (4 octets), on a p=23, q=8 (1 bit pour le signe) ce
qui permet de représenter des nombres compris, en valeur absolue, entre 2−128≈10−38 et 2128≈1038
car 128=2q=28. La précision machine est de 7 chiffres décimaux significatifs car 223=107.
11

12. Erreurs sur les calculs
On considère un nombre flottant de la forme ±a10q avec a est la mantisse de la forme 0.d1d2 · · · dt, d10, q
est l’exposant (entier relatif).
Bien sûr, l’entier q est soumis à la restriction : −M ≤ q ≤ M (où M dépend de la machine).
Cette représentation des nombres réels entraîne les conséquences suivantes :
 Il existe un plus petit nombre flottant ( zéro). Le zéro machine en valeur absolue vaut =
0.10···10−M.
 Il existe un plus grand nombre flottant, l’infinie machine et vaut = 0.99 · · ·910M.
 Tous les nombres réels n’admettent de représentation exacte :
√2 est représenté par 0.14142143×10+1
π est représenté par 0.314…×10+1
 Toute opération élémentaire (+,∗, /) est en général entachée d’une erreur.
 Une opération peut avoir un résultat non représentable :
 Si pour le résultat q > M (OVERFLOW ou dépassement de capacité.)
 Si pour le résultat q < −M (UNDERFLOW).
 La représentation flottante d’un nombre peut être obtenue à partir de sa représentation décimale par
 – la troncature (on garde les t premiers décimaux)
 – l’arrondi : le tième chiffre de la mantisse est choisi au plus près.
MANIPULATION
Supposons par exemple que les réels soient calculées avec 3 chiffres significatifs et arrondis à la décimale
la plus proche. Soit à calculer la somme x+y+z avec x = 8,22, y= 0,00317, z= 0,00432.
12

13. Systèmes linéaires
Soit à résoudre un système linéaire de n équations à m inconnues, ceci consiste à trouver m nombres,
réels ou complexes, x1, · · · , xm, tels que :
a11x1 + a12x2 + · · · + a1mxm = b1
a21x1 + a22x2 + · · · + a2mxm = b2
...
. . .
...
an1x1 + an2x2 + · · · + anmxm = bn
Ce système peut être réduit en une écriture matricielle AX = b. Les aij sont les coefficients, composantes de
la matrice A alors que les bj sont les composantes du vecteur second membre b. (les aij et les bj  à  ou
C. Les méthodes permettant de résoudre ce type de systèmes (m=n) sont de trois catégories :
Pour n3, par substitution ou la méthode de CRAMER.
Méthodes dites directes, comme de GAUSS ou GAUSS-JORDAN
Méthodes dites itératives, comme celle de GAUSS-SEIDEL, RELAXATION, LU, CHOLESKI.
Mathématicien
Gabriel CRAMER
1704-1752
Mathématicien
Carl Friedrich Gauss
1777–1855
Mathématicien
Philipp Ludwig von Seidel
1821–1896
Mathématicien
Camille Jordan
1838–1922
Mathématicien, Topographe
André Louis CHOLESKY
1875-1918
13

14. Systèmes linéaires (Méthode directe)
Soit à résoudre un système linéaire de n équations à n inconnues, ceci consiste à trouver n nombres, réels
ou complexes, x1, · · · , xn, tels que :
a11x1 + a12x2 + · · · + a1nxn = b1
a21x1 + a22x2 + · · · + a2nxn = b2
. . .
an1x1 + an2x2 + · · · + annxn = bn
La méthode de Gauss consiste à déterminer une matrice P telle que le système équivalent PAX = Pb soit
triangulaire supérieure et donc simple à résoudre. La résolution d’un système triangulaire supérieure est
aisée par la procédure de remontée.
Algorithme de l’élimination de GAUSS AX=b
Pour k=1 jusqu’à n-1
Pivot  akk
Si pivot0 Alors
Pour i=k+1 jusqu’à n faire
bibi – (aik/pivot)*bk
Pour j=k+1 jusqu’à n faire
aijaij – (aik/pivot)*akj
Fin j
Fin i
Sinon ‘Problème’
Fin k
Algorithme de la remontée UY=f
U Triangulaire supérieure
Pour i=n à 1 pas de -1 faire
s=fi
pour j=i+1 à n faire
s=s-uij*yj
fin j
yi=s/uii
fin i
14

15. Systèmes linéaires
Soit le programme équivalent en FORTRAN 95
PROGRAM Gauss
! Solution d’un system de N équations linéaires
! Forme matricielle A.X = B
! Déclaration des variables utilisées.
PARAMETER (IN=20)
REAL*8:: A(IN,IN), X(IN), B(IN), F, SUM1
INTEGER:: K, I, J, N, IN
! Lecture et saisie des coefficients de A et de C
PRINT *, "Introduire le nombre d‘équations (N):"
READ (5,*) N
PRINT *,"Introduire les coefficients de la matrice [A(I,J)]:"
READ (5,*) ((A(I,J),J=1,N),I=1,N)
PRINT *,"Introduire les composantes du vecteur [B(I)]:"
READ (5,*) (B(I),I=1,N)
! Décomposition (Elimination)
DO K = 1, N-1
DO I = K+1, N
F = A(I,K)/A(K,K)
15

16. Systèmes linéaires
DO J = K+1, N
A(I,J) = A(I,J) - F * A(K,J)
ENDDO
B(I) = B(I) - F * B(K)
ENDDO
ENDDO
! Remontée
X(N) = B(N) / A(N,N)
DO I = N-1, 1, -1
SUM1 = 0.0
DO J = I+1, N
SUM1 = SUM1 + A(I,J) * X(J)
ENDDO
X(I) = (B(I) - SUM1)/A(I,I)
ENDDO
! Impression des résultats
PRINT *,"Solution du problème AX=B"
WRITE (6,*) ("X(",I,")=",X(I),I=1,N)
STOP
END PROGRAM Gauss 16

17. Systèmes linéaires
La manipulation sous OCTAVE (mode commande en ligne)
octave:##> A=[1 1;2 -3]
octave:##> b=[3 5]‘ %l’apostrophe-transposé
octave:##> inv(A)*b
ans =
2.8000
0.2000
octave:##>> A*ans %Pour vérifier
ans =
3.0000
5.0000
octave:##> Ab %L’antislash
ans =
2.8000
0.2000
La condition nécessaire pour que le système ait une solution est que le déterminant soit différent de zéro.
Vérifier avec :
A=[1 1 1; 2 0 3; 3 1 4] et b = [ 2 5 6]T
A=[1 1; 1 1.01]; b=[2; 2.01]; (On changera A(1,2)=1.005;)
On utilisera les fonctions det, rank, pinv et cond, Discuter.
Exécution du
programme Gauss
17

18. Systèmes linéaires
La manipulation sous OCTAVE (mode commande en ligne)
>> A=[1 1 1; 2 0 3; 3 1 4]
A =
1 1 1
2 0 3
3 1 4
>> det(A)
ans = 5.5511e-016
>>rank(A)
ans = 2
>> A=[1 1; 1 1.01]
A =
1.0000 1.0000
1.0000 1.0100
>> b=[2; 2.01]
b =
2.0000
2.0100
>> cond(A)
ans = 402.01
La condition nécessaire pour que le système ait une solution est que le déterminant
soit différent de zéro. Vérifier avec :
A=[1 1 1; 2 0 3; 3 1 4] et b = [ 2 5 6]T
A=[1 1; 1 1.01]; b=[2; 2.01]; (On changera A(1,2)=1.005;)
On utilisera les fonctions det, rank, pinv et cond, Discuter.
18

19. Systèmes linéaires
La manipulation sous OCTAVE (mode commande en ligne)
>> A=[1 1 1; 2 0 3; 3 1 4]
A =
1 1 1
2 0 3
3 1 4
>> b = [2 5 6]'
b =
2
5
6
>> x=pinv(A)*b
x =
0.69048
-0.11905
1.09524
>> x=inv(A)*b
warning: matrix singular to machine precision, rcond = 1.15648e-017
x =
-5.4043e+015
1.8014e+015
3.6029e+015
>> rank(A)
ans = 2
La condition nécessaire pour que le système ait une solution est que le déterminant
soit différent de zéro, vérifier avec :
A=[1 1 1; 2 0 3; 3 1 4] et b = [ 2 5 6]T
A=[1 1; 1 1.01]; b=[2; 2.01]; (On changera A(1,2)=1.005;)
On utilisera les fonctions
det calcul du déterminant
rank Rang de la matrice
pinv Pseudo-Inversion de la matrice
cond conditionner une matrice.
19

20. Systèmes linéaires (Organigramme de Gauss)
La méthode de Gauss est généralement dite méthode d’élimination. Son organigramme est le suivant :
20

21. Systèmes linéaires (Méthode directe)
Soit à résoudre un système linéaire de n équations à n inconnues, ceci consiste à trouver n nombres, réels
ou complexes, x1, · · · , xn, tels que :
a11x1 + a12x2 + · · · + a1nxn = b1
a21x1 + a22x2 + · · · + a2nxn = b2
. . .
an1x1 + an2x2 + · · · + annxn = bn
La méthode de Gauss-Jordan se base sur deux transformations, une réduction suivie par une
normalisation. Ce qui consiste transformer le système AX = b en UY=F, F est triangulaire supérieure.
Pour k allant de 1 à n
Si existe une ligne ik telle que (aik)k-10 :
échanger cette ligne i et la ligne k (li  lk)
Pour i allant de 1 à n et ik
Sinon A n'est pas inversible, abandonner (on sait ici que le rang de
la matrice est k − 1).
Après l'étape k de l'algorithme, la colonne k a tous ces coefficients
nuls sauf un : celui de la diagonale, qui vaut 1.
1
1
1 

 k
kk
kk
k
k l
a
l
k
k
k
ik
k
i
k
i lall 11 

21

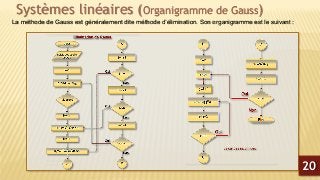
22. Systèmes linéaires (Programme Gauss-Jordan F95-F90)
program gauss_Jordan
integer::i,j,n,k
real::pivot,s
real,allocatable::a(:,:)
real,allocatable::b(:)
! Lecture et saisie des coefficients de A et de C
PRINT *, "Introduire le nombre d'equations (N):"
READ (5,*) N
allocate(A(N,N),B(N))
PRINT *,"Introduire les coefficients de la matrice
[A(I,J)]:"
READ (5,*) ((A(I,J),J=1,N),I=1,N)
PRINT *,"Introduire les composantes du vecteur
[B(I)]:"
READ (5,*) (B(I),I=1,N)
do k=1,N,1
do i=1,n,1
if (k==i) then
pivot=a(i,k)
do j=k,n,1
a(i,j)=(a(i,j))/(pivot)
end do
b(k)=(b(k))/(pivot)
else
pivot=a(i,k)
do j=k,n,1
a(i,j)=a(i,j)-pivot*a(k,j)
end do
b(i)=b(i)-pivot*b(k)
end if
end do
end do
!calcul de la solution
do i=n,1,-1
do j=i-1,1,-1
s=a(j,i)
do k=j,n,1
a(j,k)=a(j,k)-s*a(i,k)
end do
b(j)=b(j)-s*b(i)
end do
end do
do i=1,n,1
write(*,*) "x)",i,")=",b(i)
end do
write(*,*)« Matrice identité"
write(*,*) a
end program gauss_Jordan 22

23. Systèmes linéaires (Programme Gauss-Jordan F95-F90)
Pour le problème suivant :
x1 – x2 + 2x3 = 5
3x1 + 2x2 + x3 = 10
2x1 - 3x2 - 2x3 = -10
Et dont la solution est :
x1 = 1
x2 = 2
x3 = 3
Pour le problème suivant :
2x1 + x2 - x3 = 8
-3x1 - x2 + 2x3 = -11
-2x1 + x2 + 2x3 = -3
Et dont la solution est :
x1 = 2
x2 = 3
x3 = -1
23

24. Systèmes linéaires (Programme Gauss-Jordan F95-F90)
Pour le problème suivant :
x1 – x2 + 2x3 = 5
3x1 + 2x2 + x3 = 10
2x1 - 3x2 - 2x3 = -10
Et dont la solution est :
x1 = 1
x2 = 2
x3 = 3
Pour le problème suivant :
2x1 + x2 - x3 = 8
-3x1 - x2 + 2x3 = -11
-2x1 + x2 + 2x3 = -3
Et dont la solution est :
x1 = 2
x2 = 3
x3 = -1 Sous Octave
Sous CodeBlock
>> a=[2 1 -1; -3 -1 2; -2 1 2]
a =
2 1 -1
-3 -1 2
-2 1 2
>> x = mldivide(a,b)
x =
2.00000
3.00000
-1.00000 24

25. Systèmes linéaires (Organigramme Gauss-Jordan)
25

26. Systèmes linéaires (Méthodes itératives)
Soit à résoudre un système linéaire de n équations à n inconnues, ceci consiste à trouver n nombres, réels
ou complexes, x1, · · · , xn, tels que :
a11x1 + a12x2 + · · · + a1nxn = b1
a21x1 + a22x2 + · · · + a2nxn = b2
. . .
an1x1 + an2x2 + · · · + annxn = bn
Beaucoup de méthodes dont la stratégie est de commencer par un vecteur estimé initial et ainsi faire des
traitements du système à cette base (estimé initial X0) pour en déduire la solution rechechée.
(b1 - a12x2 + · · · + a1nxn)/a11 = x1
(b2 - a21x1 + · · · + a2nxn)/a22 = x2
. . .
(bn - an1x1 + an2x2 + · · · + ann-1xn-1)/ann = xn
Ou
(b1 - {j; j[1,n]/j1}a1jxj)/a11 = x1
(b2 - {j; j[1,n]/j2}a2jxj)/a22 = x2
. . .
(bn - {j; j[1,n]/jn}anjxj)/ann = xn
La formule résumée est donnée par
(bi - {j; j[1,n]/ji}aijxj)/ai,i = xi 26

27. Systèmes linéaires (Méthodes itératives- méthode Gauss-Seidel)
Donc pour un estimé initial à k=0 donc X0=(x0
1, · · · , x0
n)T, nous avons :
(bi - {j; j[1,n]/ji}aijx(k)
j)/ai,i = xi
(k+1)
Pour k, nous pouvons espérer satisfaire les transformations successives qui améliorerons la recherche
du vecteur solution X(k) en dépendance de valeurs précédentes du vecteur estimé X(k-1).
L’algorithme global de la méthode est donné dans l’encadré suivant.
La condition d’arrêt du phénomène de transformation est définie par :
|X(k) – X(k-1)|11 ou |(X(k) – X(k-1))/X(k)|21 avec 1 et 2 des valeurs réelles petites.
1: Début
2: Lecture de la matrice des coefficients A et du vecteur second membre b
3: Lecture de Eps1
4: Proposition de l’estimé initial X0
5: k=0
6: Sauvegarde de Xs=X(k)
7: Pour i=1 jusqu’à n
(bi - {j; j[1,n]/ji}aijx(k)
j)/ai,i = xi
(k+1)
8: Fin de pour
9: xmax=max{|X(k+1)-X(k)|}
10: Si xmax1 alors Impression de X(k+1); Arrêt
11: Sinon aller à (7) 27

28. Systèmes linéaires (Méthodes itératives- méthode Gauss-Seidel)
Donc pour un estimé initial à k=0 donc X0=(x0
1, · · · , x0
n)T, nous avons :
(bi - {j; j[1,n]/ji}aijx(k)
j)/ai,i = xi
(k+1)
Pour k, nous pouvons espérer satisfaire les transformations successives qui améliorerons la recherche
du vecteur solution X(k) en dépendance de valeurs précédentes du vecteur estimé X(k-1).
L’algorithme global de la méthode est l’encadré suivant.
La condition d’arrêt du phénomène de transformation est définie par :
|X(k) – X(k-1)|11 ou |(X(k) – X(k-1))/X(k)|21 avec 1 et 2 des valeurs réelles petites.
Program Gseidel
parameter(ITERMAX=500) ! Nombre maximal des itérations
Integer:: N, Iter, i, j, Sol
Real,allocatable:: A(:,:)
Real,allocatable:: X(:), B(:)
Real Xs, Dmax, Eps
! Lecture et saisie des coefficients de A et de C
PRINT *, "Introduire le nombre d‘équations (N):"
READ (*,*) N
allocate(A(N,N),B(N),X(N))
PRINT *,"Introduire les coefficients de la matrice [A(I,J)]:"
READ (*,*) ((A(I,J),J=1,N),I=1,N)
28

29. Systèmes linéaires (Méthodes itératives- méthode Gauss-Seidel)
PRINT *,"Introduire les composantes du vecteur [B(I)]:"
READ (*,*) (B(I),I=1,N)
! Saisie de l’estimé initial
PRINT *,"Introduire le vecteur estime initial [X(0)]:"
READ (*,*) (X(I),I=1,N)
PRINT *,"Introduire la valeur du Epsilon"
READ (*,*) Eps
! Initialisation des itérations
Iter=0
Dmax=0.
Sol=2
do while (Sol == 2)
Do i=1,N
Xs = X(i)
S=0
Do j=1,N
If (j /= i) then
S = S + A(i,j)*X(j)
End if
End do
X(i) = (B(i)-S)/A(i,i)
Xs = ABS(X(i) - Xs)
… Suite
29

30. Systèmes linéaires (Méthodes itératives- méthode Gauss-Seidel)
! Test sur la valeur de l’écart par rapport à Dmax
If (Xs > Dmax) then
Dmax = Xs
End if
End do
If (Dmax > Eps) then
Iter=Iter + 1
If (Iter>ITERMAX) Then
Sol=-1
End if
Else
! Le calcul converge, solution existe
PRINT *, "Vecteur solution X est donne par :"
Do i=1,N
Print *,"X(",i,") = ",X(i)
End do
Sol=0
End if
End do
End program GSeidel
Soit l’exemple suivant avec X(0)=0
4x1 + x2 - x3 = 3
2x1 + 7 x2 + x3 = 19
x1 - 3 x2 +12 x3 = 31
… Suite
30

31. Systèmes non-linéaires (Méthode variationnelle)
Un système d’équations non linéaires SENL (ζ) est la composition
faite de m équations non-linéaires :
f1(X) = 1(X)
f2(X) = 2(X)
….
fm(X) = m(X)
où X={x1, x2, … xp} sont les p inconnues du système alors que 1, 2, … ,n sont les m fonctions du second
membre, elles même dépendantes de X. Géométriquement, les m équations représentent les m courbes
(α, β, …) en intersection dans un référentiel R n.
Les systèmes non linéaires sont plus difficiles à étudier que les systèmes linéaires. Néanmoins, en
linéarisant (cas de systèmes linéarisable) un SNL, autour d'un point A de considération finie (situation ou
état du système), on obtient un système linéaire qui correspond à une approximation grossière du système
non linéaire d’origine. Cette approche a atteint sa maturité dans le livre de H.W.Bode (1905-1982) à la fin de
la IIème guerre mondiale. Les travaux de R.E.Bellman (1920-1984), L.S.Pontryagin et al (1908-1988) surtout
de R.Kalman (1930) ont conduit, nombre d'automaticiens à privilégier la représentation d‘espace d’état à
partir des années 1960. Un système est non linéaire s’il se comporte non linéairement par rapport à ses
composantes intrinsèques.
Bode
Bellman KalmanPontryagin
31

32. Systèmes non-linéaires (Méthode variationnelle)
PRINCIPE DE LA LINEARITE DES SYSTEMES
Principe de proportionnalité : si s(t) est la réponse à l'entrée e(t)
alors λ*s(t) est la réponse à l'entrée λ*e(t).
Principe de superposition : si s1(t) est la réponse à l'entrée e1(t)
et s2(t) est la réponse à l'entrée e2(t) alors [s1(t) + s2(t)] est la
réponse à l'entrée [e1(t) + e2(t)].
Allure de la courbe d’un SNL : pour un système NON linéaire,
en régime nominal (en fonctionnement normal et sans
excitation perturbatrice), la courbe s = f(e) n’est pas une
droite. Un système SNL est continu, par opposition à un SNL
dit discret, lorsque les variations de ses composantes sont
continûment observable dans le cadre de son domaine de
définition δ.
Un système est invariant (stationnaire) si ses caractéristiques
sont insensibles aux changements du temps.
selon ces faits, le système linéaire SL reflète les mêmes
réactions indépendamment du temps.
La forme d’équation donnée par :
f(X) = C
Est dite non linéaire si elle n’est pas une application linéaire
vérifiant les condition de superposition et de proportionnalité.
L'équation est dite homogène si C=0.
Le définition f(X)=C est très générale au même moment que X
peut être toute composante du système sensible
mathématiquement (nombre, vecteur, fonction, … etc.), et
l’expression de f(X) peut avoir littéralement beaucoup de
formes, une forme récurrente, l'intégrale ou différentielle avec
association de contraintes (telles que les valeurs
initiales/limites). Si f(x) contient une différenciation par rapport
à X, le résultat sera une équation différentielle.
Une équation algébrique (polynomiale) non linéaire
donnée par
a.x3+b.x-3=0
Une équation non linéaire itérative est toujours la
résultante d’une écriture de type :
u(k+1) = g(u(k))
Une équation différentielle, quant à elle est donnée
par :
du/dx=-A*u3.
32

33. Systèmes non-linéaires (Méthode variationnelle)
Modélisation d’un système d’équation non-linéaires
Soit F={fi; i[1, m]} un système de fonctions non linéaires des n variables xk (tel que k[1, n]) définit dans un
domaine D résultant de l’union de p sous-domaine dj, D={dj; j[1, p]}.
On définit par :
F(X)=K un problème non linéaire (SNL) à résoudre. Si K est équivalente au vecteur 0, F est dit homogène. Si C
est l’ensemble des ci contraintes définies, chacune sur un domaine dj. F(X) peut être régit par C, dans ce cas on
parle de problème non linéaire contraint.
Dans le cas où le paramètre K est égal 0 et C est vide (C=), F(X) admet des zéros A(a0, a1, …, an) dans D.
Par la méthode de Newton-Raphson (NR), nous admettons, qu’autour d’un point X0, F(X) peut être explicitée par
son développement limité au sens Taylor et dont la forme est :
F(X0+DX0)  F(X0)+(1/1!).[F(X)X=Xo].X0+…+(X0)
D’où X0 est la plus bonne estimation de X* (solution exacte du problème), F(X) est dite NABLA F, Gradient du
système de fonctions fi, X0 étant l’écart entre X* et X0 et finalement (X0) représente le reste de Taylor, 
regroupe les dérivées d’ordres supérieur à 1 jusqu’à  (l’infini).
Si l’estimation est justifiée, (X0) tendra vers 0, puisque les termes 1/n! tend vers 0 (pour n≥2) quant n.
De ce fait on garde seulement la partie;
F(X0+X0)  F(X0)+(1/1!).[F(X)X=Xo].X0, (X0)  0
Et puisque F(X) est supposée égale à 0, nous aurons
F(X0)+(1/1!).[F(X)X=Xo].X0  0  [F(X)X=Xo].X0  - F(X0)
Si on note (F(X)X=Xo)=J(X0) on a J(X0).X0  - F(X0) d’où X0  - [J(X0)]-1.F(X0) et X = X0+X0.
33

34. Systèmes non-linéaires (Méthode variationnelle)
Formalisation
Pour un système F(X)=f(x)=0 (Cas de système à une fonction à une variable), nous avons :
f(x) = 0  f(x) = f(x0 + h) ≈ f(x0) + (f(x))’
(x0) .h, avec h=(x-x0).
x ≈ x0 + h ≈ x0 + f(x0)/(f(x0))’
Graphiquement, L’estimé initial est pris comme première
approximation de la solution, alors, par récurrence h est
recalculer de manière à corriger (par une quantité h  f(x0)/(f(x0))’)
pour un sens de déplacement pour ainsi atteindre la solution.
De manière générale, nous calculerons J(X0) dite matrice
Jacobéenne du système.
X = X0 + X0 = X0 + (- [J(X0)]-1.F(X0)])
La formule de récurence donne les estimés successifs;
Xk+1 = Xk + Xk = Xk + (- [J(Xk)]-1.F(Xk)])
Le calcul est arrêté si et seulement si Xk tend vers zéro ou est
assimilable à une petite valeur 1 en valeur absolue (|Xk| 1).
ou encore (|Xk / Xk+1| 2). Ces deux conditions sont dites CONDITIONS D’ARRET, et le
déterminant de
de J est Jacobéen (|J(X)|). 34

35. Systèmes non-linéaires (Méthode variationnelle)
Problème type :
Un fournisseur de service GSM veut développer une nouvelle stratégie en faveur de ses
clients de marque. Pour cela, il pensa à vérifier si les emplacements de ses cellules
(antennes et équipements afférents) sont dans les recommandations optimales de
localisation. La répartition de ses clients dépend des localités où ceux-ci exercent leur
activités. La nouvelle stratégie consiste à favoriser le client selon un profil des activités
contractées et en cours avec le fournisseur. Pour cela, répartir les antennes d’une
manière optimale selon la distance la plus courte possible des clients en question.
Formalisation
D={dip} : Vecteurs des distances qui séparent les différents antennes ai de l’antenne
principale ap(au nombre de m composantes)
xi ,yi : étant les coordonnées du point ai d’une antenne. La distance est donnée par :
dij = ([(xj-xi)2+(yj-yi)2]^(1/2)) : distance d’un point i à un point j
S=dij
2 : Somme des distances à minimiser représente la fonction à optimiser.
Conditions de couverture, zone d’ombre (conditions techniques)
Représentation graphique du problème de la
localisation optimale des antennes.
Exemple d’antenne utilisées pour les GSM.
35
Processus de convergence des valeurs
de x vers la solution x*

36. Systèmes non-linéaires (Méthode variationnelle)
Problème type :
Un fournisseur de service GSM veut développer une nouvelle stratégie en faveur de ses
clients de marque. Pour cela, il pensa à vérifier si les emplacements de ses cellules
(antennes et équipements afférents) sont dans les recommandations optimales de
localisation. La répartition de ses clients dépend des localités où ceux-ci exercent leur
activités. La nouvelle stratégie consiste à favoriser le client selon un profil des activités
contractées et en cours avec le fournisseur. Pour cela, répartir les antennes d’une
manière optimale selon la distance la plus courte possible des clients en question.
36
L’algorithme NR est donné par :
1. Demander X0, 
2. Mettre k=0
3. Répéter
4. Evaluer Xk+1 (à la précision désirée)
5. Si (f ’(Xk) = 0) alors Terminer
a) Xk=Xk+1
b) Xk+1 = Xk +(- [J(Xk)]-1.F(Xk)])
6. Tant que Xk≥
7. Afficher Xk+1
La méthode NR est l’une des méthode les plus simple à implémenter, très simple
d’utilisation et efficace numériquement. Beaucoup de variantes existent
(Fletcher-Powell, Bellman, …)
Isaac NEWTON
(1642 −1727)
Joseph Raphson
(1648-1715)
Processus de convergence des valeurs
de x vers la solution x*

37. program NR
! Déclaration
real, parameter::error =1e-4
integer::k
real::xo,x1,f,fd
! Debut du traitement
read*,xo
k=1
10 x1=xo-(f(xo)/fd(xo))
if (abs((x1-xo)/x1)<error)then
print*,"racine est égale a ", x1 , " obtenue en iteration=", k
else
xo=x1
k=k+1
goto 10
endif
End program NR
real function f(x)
real::x
f = x**3-x-1
End
real function fd(x)
real::x
fd = 3*x**2-1
End
Systèmes non-linéaires (Méthode variationnelle)
Cas de fonction à une variable :
Soit la fonction :
f(x)= x3-x-1
Il est nécessaire de décider sur le sort de
la valeur initiale afin de déterminer la
racine. L’illustration graphique peut dans
ce cas simple aider. On note que
f(1)=−1<0 alors que f(2)=5>0. Cependant,
la racine pour f(x)=0 doit existée dans
l’intervalle [1, 2].
Si on prend x0=1 en tant que valeur initial.
Nous pouvant déterminer la solution en
utilisant la méthode NR.
Selon la méthode NR, nous détermineront
que la racine de f est 1.324718 à 6
décimales.
37
Valeur initiale x0

38. program NR
real, parameter::error =1e-4
integer::k
real::xo,x1,f,fd
read*,xo
k=1
10 x1=xo-(f(xo)/fd(xo))
if (abs((x1-xo)/x1)<error)then
print*,“La racine est égale a “
print*, x1
print*, " obtenue en iteration=", k
else
xo=x1
print*,“Estime suivant “, x1, “ iteration=", k
k=k+1
goto 10
endif
End program NR
real function f(x)
real::x
f = x**3-x-1
End
real function fd(x)
real::x
fd = 3*x**2-1
End
Systèmes non-linéaires (Méthode variationnelle)
Cas de fonction à une variable :
Soit la fonction :
f(x)= x3-x-1
Il est nécessaire de décider sur le sort de
la valeur initiale afin de déterminer la
racine. L’illustration graphique peut dans
ce cas simple aider. On note que
f(1)=−1<0 alors que f(2)=5>0. Cependant,
la racine pour f(x)=0 doit existée dans
l’intervalle [1, 2].
Si on prend, maintenant x0=4 en tant que
valeur initial. Nous pouvant déterminer la
solution en utilisant la méthode NR.
Nous aurons 1.324718 comme racine de f.
Valeur initiale x0
38

39. Interpolation & approximation (Statistique, Lissage, Extrapolation)
Interpolation des fonctions :
39

40. MERCI POUR VOTRE ATTENTION
Fin du douzième chapitre
A suivre …
40

41. Références
L.-V. Bertallanfy, ‘General System Theory’, Edition MASSON, 1972.
41