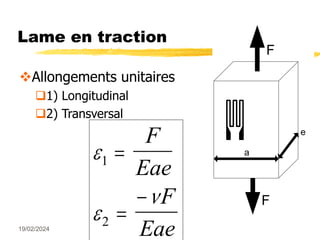
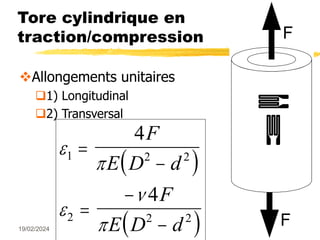
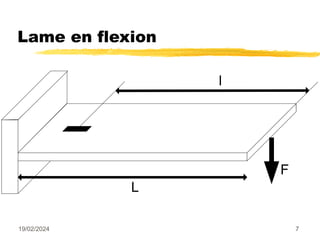
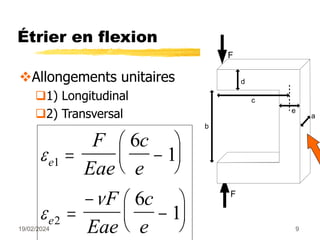
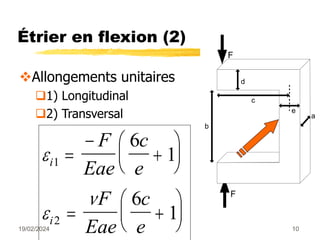
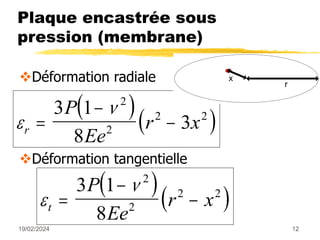
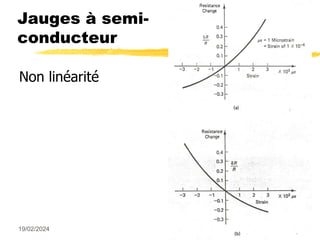
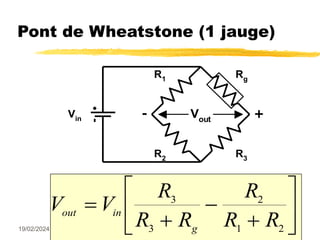
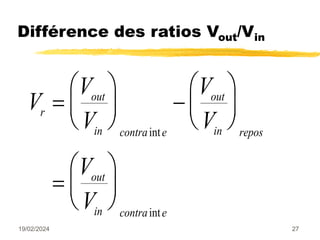
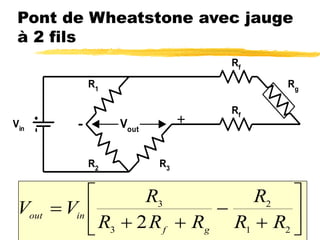
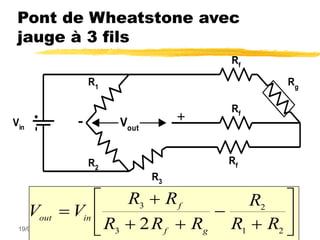
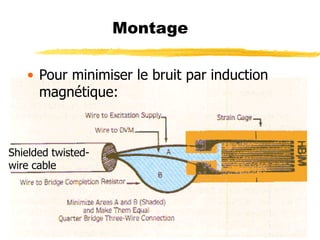
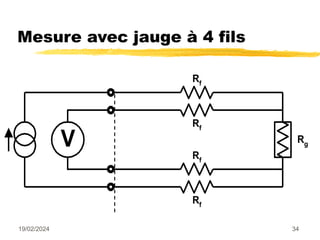
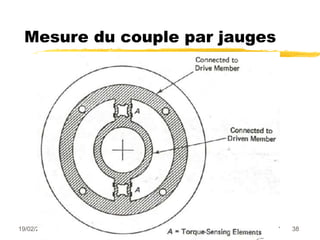
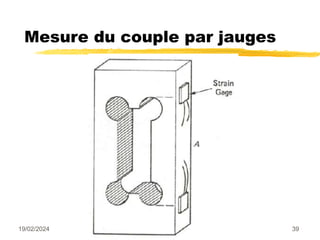
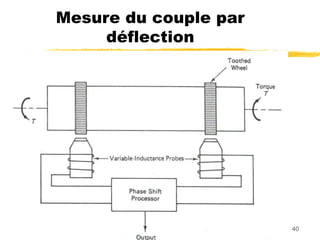
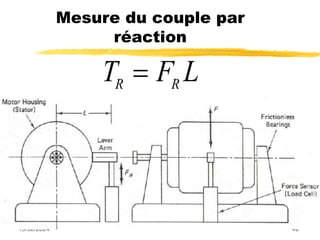
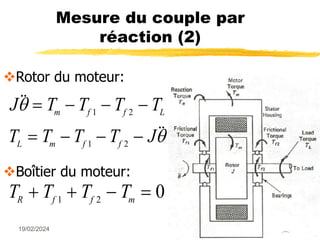
Le document traite des mesures de force, de couple et de pression, en expliquant différents modes de transduction tels que résistif, piézoélectrique, capacitif et inductif. Il détaille également le fonctionnement des jauges de contrainte ainsi que des méthodes de mesure de couple, y compris par jauges et déflexion. Enfin, il présente un bilan comparatif des jauges métalliques et à semi-conducteurs en termes de précision et d'application.

1. 19/02/2024 1
Mesure
de force, couple et pression
Partie A
Automne 2007

2. 19/02/2024 2
Mode de transduction
Transduction résistive:
Potentiomètre
Jauge extensiométrique (de contrainte)
Métallique ou Semi-conducteur
Transduction piézoélectrique
Transduction capacitive

3. 19/02/2024 3
Mode de transduction (2)
Transduction inductive:
LVDT
Courant de Foucault
Balance de force
Transduction électromagnétique
magnétostriction

4. 19/02/2024 4
Corps d’épreuve
Force, poids, couple:
Tige encastrée (lame en flexion)
jauge extensiométrique
Poutre en S
jauge extensiométrique
Ressort
potentiomètre, LVDT, courant de Foucault
Poutre avec magnétostriction

5. 19/02/2024 5
Lame en traction
Allongements unitaires
1) Longitudinal
2) Transversal
a
e
F
F



1
2



F
Eae
F
Eae

6. 19/02/2024 6
Tore cylindrique en
traction/compression
Allongements unitaires
1) Longitudinal
2) Transversal
 
 





1 2 2
2 2 2
4
4





F
E D d
F
E D d F
F

7. 19/02/2024 7
Lame en flexion
F
L
l

8. 19/02/2024 8
Lame en flexion (2)
Allongements unitaires
1) Longitudinal
2) Transversal



1 2
2 2
6
6



Fl
Eae
Fl
Eae
F
L
l

9. 19/02/2024 9
Étrier en flexion
Allongements unitaires
1) Longitudinal
2) Transversal



e
e
F
Eae
c
e
F
Eae
c
e
1
2
6
1
6
1
 















F
a
b
c
d
e
F

10. 19/02/2024 10
Étrier en flexion (2)
Allongements unitaires
1) Longitudinal
2) Transversal



i
i
F
Eae
c
e
F
Eae
c
e
1
2
6
1
6
1









 






F
a
b
c
d
e
F

11. 19/02/2024 11
Corps d’épreuve (2)
Pression:
Tube borgne
Jauge extensiométrique
Membrane:
Piézoélectrique, jauge ext., capacitive
Capsule anéroïde et souflet
Potentiomètre, LVDT, Courant de Foucault
Tube de Bourdon
Potentiomètre, LVDT, Courant de Foucault

12. 19/02/2024 12
Plaque encastrée sous
pression (membrane)
Déformation radiale
Déformation tangentielle
 
 


r
P
Ee
r x



3 1
8
3
2
2
2 2
r
x
 
 


t
P
Ee
r x



3 1
8
2
2
2 2

13. 19/02/2024 13
Membranes (Diaphragm)
• Équation de la membrane:
• P = pression mesurée
• Pref = pression de référence
• z = déformation centrale
• E = module de Young
  = coefficient de Poisson
• e = épaisseur de la membrane
• R = rayon de la membrane
P P
Ee
R
z
e
z
e
ref
 

 

 








16
3 1
0 488
4
4 2
3
( )
.


14. 19/02/2024 14
Jauges de contraintes
(ou extensiométriques)

15. 19/02/2024 15
Principe de fonctionnement
– Résistance d'un conducteur cylindrique:
– A = section du conducteur;
– l = longueur du conducteur;
  = résistivité du conducteur;
– R = résistance du conducteur.
R
l
A



16. 19/02/2024 16
Principe de fonctionnement (2)
• Si le conducteur subit une force de
traction:
–  Effet de l'allongement:
dR
R
dl
l

Direction of sensitivity

17. 19/02/2024 17
Principe de fonctionnement (3)
Si le conducteur subit une force de
traction:
  Diminution de la section:
• Loi de Poisson ( = coefficient de Poisson)
dA
A
dl
l

2

18. 19/02/2024 18
Principe de fonctionnement (4)
• Si le conducteur subit une force de
traction:
–  Effet de piézorésistivité:
– C = constante de Brigman
d CdV
V
C
dl
l



  
( )
1 2

19. 19/02/2024 19
Équation complète
Si le conducteur subit une force de
traction:
Au total ces trois effets donnent:
 
dR
R
C
dl
l
   
1 2 1 2
 
( )

20. 19/02/2024 20
Équation simplifiée
• Donc:
• Et G est le facteur de jauge.
– variant de 1.8 à 2.4 chez les conducteurs;
– variant de 50 à 200 chez les semi-
conducteurs.
dR
R
G
dl
l


21. 19/02/2024 21
Déformation unitaire
– Unité de mesure exprimant la déformation
et exprimée en "strain" ();
– 1  = déformation de 1 m par mètre;
– de 0.1 à 40 000  chez les conducteurs;
– de 0.001 à 0.003  pour les semi-cond.
• Ainsi, on peut écrire: R = Ro (1 + G)

22. 19/02/2024 22
Jauges à semi-
conducteur
Non linéarité

23. 19/02/2024 23
Exemple
– R = 120 , G = 2 et  = 1 .
• dR = 120 x 2 x 1x 10-6 = 240 
• (Oui, Vous avez bien lu...)
• Un pont de Wheatstone pourra mesurer
une telle variation de résistance.

24. 19/02/2024 24
Pont de Wheatstone (1 jauge)
Rg
Vin
R2
R1
R3
Vout
V V
R
R R
R
R R
out in
g










3
3
2
1 2
+
-

25. 19/02/2024 25
Pont équilibré
Si R1 = R2 = R3 = Rg = R (pont équilibré):
V V
R
R R
R
R
V
R
R R
out in
in









 







2 2
2 2



( )

26. 19/02/2024 26
Pont équilibré (2)
En l’absence de contraintes
R=0, donc Vout = 0 Volt

27. 19/02/2024 27
Différence des ratios Vout/Vin
V
V
V
V
V
V
V
r
out
in contra e
out
in repos
out
in contra e






 













int
int

28. 19/02/2024 28
Calcul de la déformation
 


4
1 2
V
G V
r
r
( )

29. 19/02/2024 29
Pont de Wheatstone avec jauge
à 2 fils
V V
R
R R R
R
R R
out in
f g

 








3
3
2
1 2
2
Vin
R2
R1
R3
Vout
Rg
Rf
Rf
+
-

30. 19/02/2024 30
Calcul de la déformation
 









4
1 2
1
2
V
G V
R
R
r
r
l
g
( )

31. 19/02/2024 31
Pont de Wheatstone avec
jauge à 3 fils
V V
R R
R R R
R
R R
out in
f
f g


 








3
3
2
1 2
2
Vin
R2
R1
R3
Vout
Rg
Rf
Rf
Rf
+
-

32. 19/02/2024 32
Pont de Wheatstone avec
jauge à 2 ou 3 fils
Rf introduit
une erreur
de mesure

33. 19/02/2024 33
Montage
• Pour minimiser le bruit par induction
magnétique:
Shielded twisted-
wire cable

34. 19/02/2024 34
Mesure avec jauge à 4 fils
Rg
Rf
Rf
V
Rf
Rf

35. 19/02/2024 35
Bilan (Jauges métalliques)
• Bonne précision;
• Plage d'utilisation en température
étendue;
• Électronique de traitement simple (pont
de R);
• Facteur de Jauge faible;
• Problème de vieillissement de la colle.

36. 19/02/2024 36
Bilan (Jauges à semi-
conducteurs)
• Très bonne précision;
• Facteur de jauge élevé (gain);
• Intégration possible des circuits de
traitement;
• Miniaturisation possible;
• Dérive importante avec la température.

37. 19/02/2024 37
Mesure de couple
- Par jauge
- Par déflexion
- Par réaction
- Par le courant

38. 19/02/2024 38
Mesure du couple par jauges

39. 19/02/2024 39
Mesure du couple par jauges

40. 19/02/2024 40
Mesure du couple par
déflection

41. 19/02/2024 41
Mesure du couple par
déflection
Ln
GJ
T


G = Module en cisaillement.
J = Moment d’inertie polaire.
L = Distance entre les capteurs.
N = Nombre de dents.
Φ = Déphasage.

42. 19/02/2024 42
Mesure du couple par
réaction
T F L
R R


43. 19/02/2024 43
Mesure du couple par
réaction (2)
Rotor du moteur:
Boîtier du moteur:
J T T T T
T T T T J
m f f L
L m f f




   
   
1 2
1 2
T T T T
R f f m
   
1 2
0

44. 19/02/2024 44
Mesure du couple par
réaction (3)
Calcul du couple :
Mesure de l’accélération nécessaire
T T J
L R
  


45. 19/02/2024 45
Mesure du couple par le
courant
Pour un moteur DC:
 ia = courant d’armature;
 if = courant de champ.
T ki i
m f a
