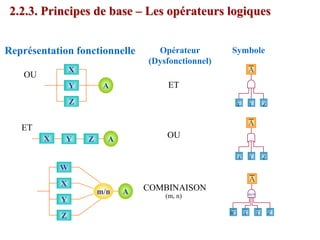
Le document traite des diagrammes de fiabilité et des arbres de causes, essentiels à la compréhension des défaillances dans les systèmes. Il aborde les concepts fondamentaux tels que les chemins, les coupes, et présente des méthodes de calcul pour évaluer la fiabilité du système ainsi que l'analyse des événements indésirables. En outre, il souligne l'importance des analyses qualitatives et quantitatives dans divers domaines comme l'aéronautique et le nucléaire.

1. Diagrammes de fiabilité
Arbres des causes
Cours DIAGNOSTIQUE ET
MAINTENANCE
2ème année MPII
AU: 2022/2023
CHAPITRE 2
Ecole Nationale d’Electronique et des
Télécommunications de Sfax
1

2. 2.1. Les diagrammes de fiabilité
Définitions
• Chemin : ensemble d'entité dont le fonctionnement
assure le fonctionnement du système.
• Chemin minimal : plus petite combinaison d'entités
assurant le fonctionnement.
• Coupe : ensemble d'éléments dont la panne entraîne la
panne du système ou encore ensemble d'éléments
coupant chaque chemin de succès.
• Coupe minimale : coupe contenant aucune autre
coupe, est un ensemble d'événements tous nécessaires
pour entraîner la panne.
2.1.1. Outils complémentaires
2

3. La probabilité que le système soit en panne est égale à celle qu'une ou
plusieurs coupes soient vraies, (panne si apparition d'une coupe)
 
1 2
1
1
m
m i
i
A R R P C C C P C

 
         
 

3

4. 1 1 1
1 2
1 1 2 1 3 2 1
( ) ( ) ( ) ( 1) ( )
j j
m m m m k
m
i i i j i j k m
i i j i j k i
P C P C P C C P C C C P C C C
  
      
 
        
 
 
   
1 2
1 1
( ) ( ) ( ) ( ) ( ) (1 )
n n
i n j j
j j
P C P E P E P E P E P R
 
     
Rj correspond à la fiabilité du composant dont la défaillance première
constitue l'événement j de la coupe i.
Sachant par ailleurs que les probabilités de coupes sont en général
faibles et d'autant plus que leur ordre est élevé et que la fiabilité des
entités est grande (la défaillance première a une probabilité = 1 -
fiabilité) :
Exemple 2 entités en série :
Si les fiabilités sont grandes alors
1 2 1 2
(1 )(1 )
R R R R R
     1 2
1 (1 )(1 )
R R R
     1 2 1 2
R R R R R
  
1 2 min1 min2
R R R C C
   
4

5. Si les fiabilités sont grandes alors
Exemple 3 entités en série :
2.1.2. Calcul de fiabilité du système par la méthode des chemins
1 2 3 1 2 3
1 2 3
1 2 1 2 3
3 1 2 1 2 1 3 2 3 1 2 3
3 1 2 1 2 1 3 2 3 1 2 3
(1 )(1 )(1 )
1 (1 )(1 )(1 )
1 (1 )(1 )
1 1
R R R R R R R
R R R R
R R R R R R
R R R R R R R R R R R R R
R R R R R R R R R R R R R
    
     
      
         
       
1 2 3 min1 min2 min3
R R R R C C C
     
Chemin Coupe
1-2
3-4
1-3
2-4
1-4
2-3
5

6. Le système fonctionne (i.e. fiable) dès que l'un au moins des sous
systèmes fonctionne (i.e. Rch
1 ou Rch
2), sa défaillance implique la
défaillance de tous les sous ensembles :
( ) où
R t P E E
 
   exprime la non défaillance du système.
1 1
1 2 1 1 1 2
( ) ou =
ch ch
i
i
R t P E E P E P E R R R
     
    
     
Chemin 1 →
Chemin 2 → 2 2
3 4 3 4 3 4
( ) ou =
ch ch
i
i
R t P E E P E P E R R R
     
    
     
Défaillance :     1 2
1 ( ) chemin1 chemin2 =(1-R )(1-R )
ch ch
R t P P
  
Fonctionnement :     1 2
( ) 1 chemin1 chemin2 =1 (1-R )(1-R )
ch ch
R t P P
   
1 2 3 4
( ) 1 (1-R R )(1-R R )
R t  
6

7. Généralisation
La fiabilité d'un système par la méthode des chemins est donnée par
l'expression suivante :
j
1 1
( ) 1 (1 chemin ) 1 (1- R )
j
k k
ch
i
j j i
R t P
 
 
       
 
où k est l'ensemble des chemins minimaux et la fiabilité du chemin j composé
de i entités en série ,
R j
ch
i
i

Remarque : Si l'ensemble des entités que forme le chemin j sont vrai
alors
R 1
j
ch
i
i
 
et donc R(t) = 1. La formule reste vraie si on ajoute aux liens minimaux
des liens non minimaux.
7

8. 1.1.3 Calcul de fiabilité du système par la méthode des coupes
Chemin Coupe
1-2
3-4
3-2
1-4
1-3
2-4
Plus fiable
que le système
précédent.
Généralisation
La fiabilité d'un système par la méthode des coupes est donnée par
l'expression suivante :
où k est l'ensemble des coupes minimales et la "non fiabilité" du système
engendré par la coupe j composé de i entités en parallèles.
1 1 1
1 3
( )
c c c
R t R R

2 2 2
2 4
( )
c c c
R t R R

Coupe 1 →
Coupe 2 →
   
1 1 2 2
2 2
j
1 1
1 3 2 4
( ) coupe1 coupe2 = (1- coupe ) (1- R )
=(1-R R )(1-R R )
j
c
i
j j i
c c c c
R t P P P
 
 
     
 
j
1 1 1
( ) (1- coupe ) (1- R )= (1- (1 )
j j
k k k
c c
i i
j j i j i
R t P R
  
 
       
 
R
j
c
i
i
 8

9.  Démarche apparue dans les années 1960 (aux EU, WASH1400
Rapport Rasmussen).
 Domaines militaire et aéronautique puis nucléaire, chimique, etc.
 Analyse de :
– fiabilité,
– disponibilité,
– sécurité.
 Apparition de cette méthode car il devenait nécessaire de prendre en
compte les combinaisons de pannes : augmentation de la sécurité
des systèmes et donc de leur complexité (ex : redondance).
 Analyses qualitatives et quantitatives.
2.2.1. Généralités
2.2. Arbre de causes ou de défaillances
9

10.  Définition de l‘Événement Indésirable (EI) fondamentale.
Nota : Événement Indésirable ou Événement Redouté.
Ex : Incendie ou Incendie 800°C – 5 minutes.
 Démarche déductive :
– Décomposition successive aux niveaux inférieurs.
 Représentation par :
– Opérateurs logiques.
– Événements.
– Symbole de transfert.
L’arbre de défaillance permet de mettre en
évidence les combinaisons de défaillances.
2.2.2. Principes de base – Bases d’élaboration
10

11. Symbole
Opérateur
(Dysfonctionnel)
ET
OU
COMBINAISON
(m, n)
A
A
A
m/n
Représentation fonctionnelle
X
Y
Z
A
X Y Z A
X
Y
Z
W
A
m/n
2.2.3. Principes de base – Les opérateurs logiques
ET
OU
X
X
X
Y
Y
Y
Z
Z
Z
W

12.  Représentations :
Combinaison d'événements
Élémentaire
Non élémentaire mais non développé
ou non développé momentanément
Événement conditionnel
2.2.4. Les événements
Case configuration
12

13.  Définitions des événements de base :
– Élémentaire :
• généralement une défaillance,
• phénomène assez connu pour ne pas le développer plus
(probabilité faible - Rex).
– Non élémentaire et non développé :
• événement étant une cause externe au système étudié (Ex :
alimentation HS),
• porte ET avec plus de 3 branches.
– Non élémentaire et non développé momentanément :
• pas de renseignements suffisants,
• à développer par un fournisseur ou à documenter.
– Case configuration :
• Permet de réaliser un seul arbre pour différentes phases de vie.
13

14.  Détermination de toutes les causes menant à l'EI :
– Événements élémentaires.
– Ils sont organisés soit en panne simple soit en combinaison de
pannes.
– Ils touchent des :
• défaillances de commande (rupture d’alimentation, défaillance
logicielle, etc.),
• défaillances intrinsèques (conception, utilisation, agression
extérieure, erreur humaine, process, etc.).
– Les défaillances prises en compte sont fonction des limites de
l’étude :
• agressions extérieures,
• problèmes de process,
• erreur humaine.
2.2.5.Recherche des causes
14

15.  Un système est soit :
Non commandé, mauvaise commande ou pas de commande. Une
commande peut être :
• Un flux : information (électrique, électromagnétique, etc.),
matière (gaz, liquide, etc.).
 ex : pas d’alimentation (carburant, électricité etc.) à l’entrée
d’un moteur. Pas de commande issue d’un calculateur.
Mauvaise information issue d’un capteur.
 Une interaction mécanique : contact, tension, support, etc.
 ex : pas de transmission du mouvement de translation
ensemble bielle/manivelle.
15

16.  Victime d’une Défaillance Intrinsèque (DI) :
• Conception (produit) (Ex : matériel inadapté, etc.).
• Fabrication (process) :
 Machine (Ex : Précision insuffisante, etc.),
 Homme (Ex : Soudure non conforme, etc.).
• Utilisation :
 Usure, prise de jeu, etc.
 Agressions extérieures (Ex : thermique, corrosion,
électromagnétisme, vibration, électrostatisme, hygrométrie, etc.)
combinées à la sensibilité du système à l’agression considérée.
 Erreur humaine (Ex : mauvaise opération, etc.).
Agression
T=40°C
Sensibilité dépassée
(T<30°C)
Agression thermique
16

17. A
B
C
D E
s
E1 E2
E
E3
C E
D
B
A
 Construction de l'arbre de défaillances
Déploiement – Démarches
17