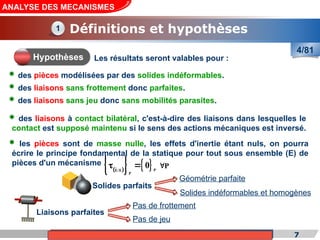
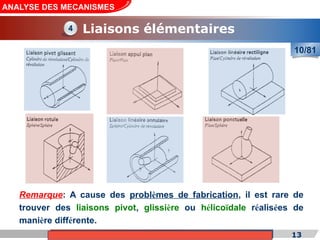
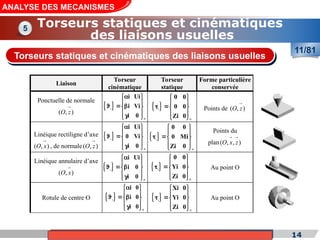
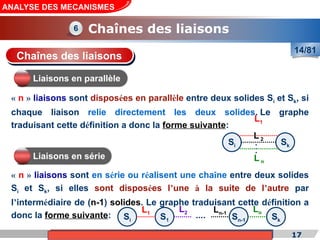
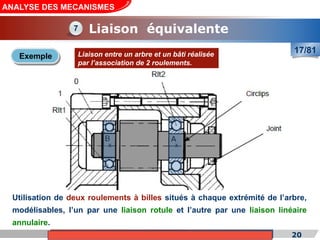
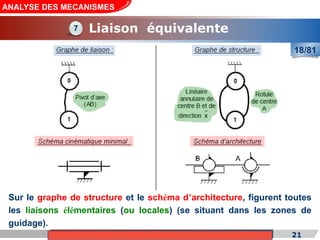
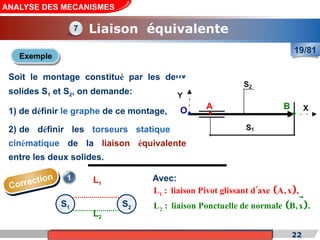
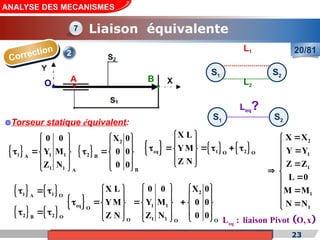
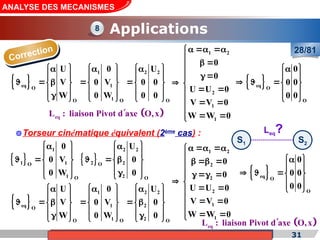
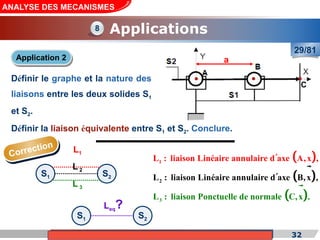
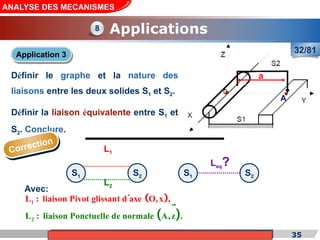
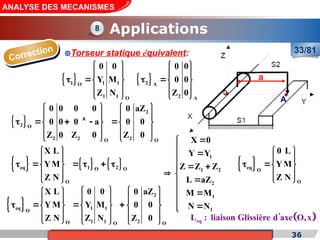
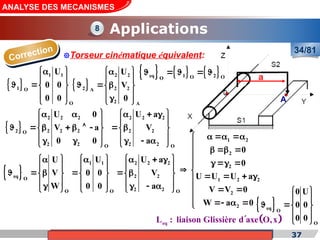
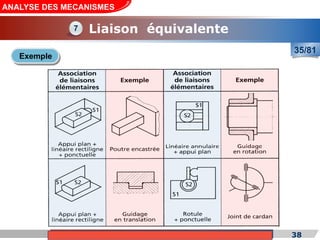
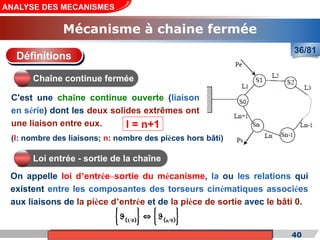
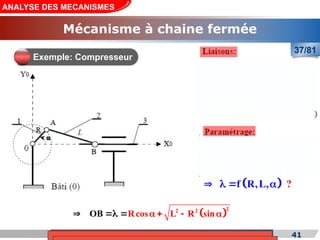
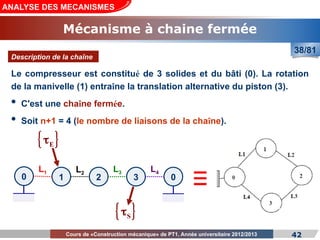
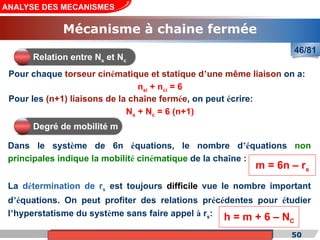
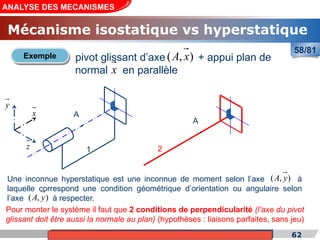
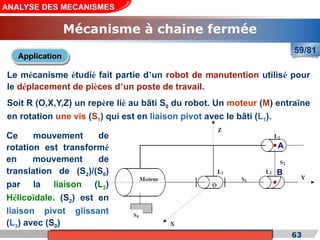
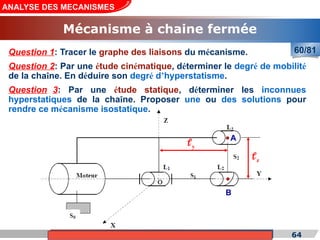
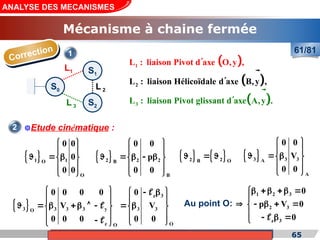
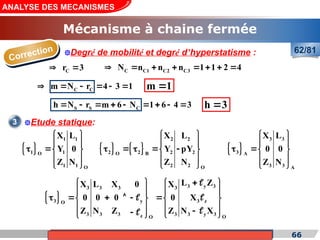
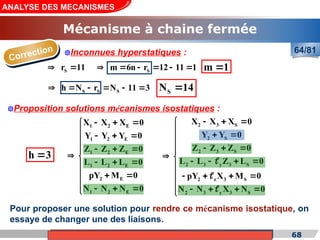
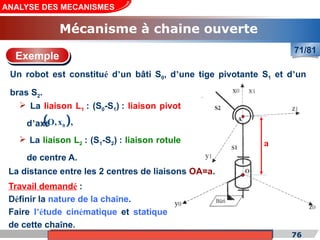
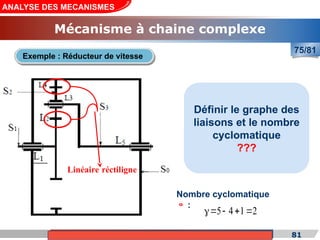
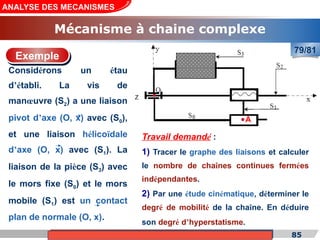
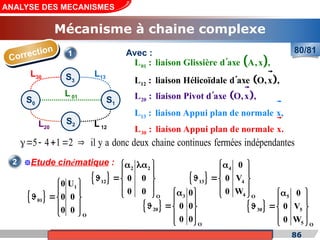
Le cours de construction mécanique de l'année universitaire 2012/2013 se concentre sur l'analyse des mécanismes et leurs applications dans la conception. Il vise à vérifier l'aptitude des mécanismes à réaliser une loi d'entrée/sortie souhaitée et à déterminer les dispositifs constructifs adéquats. Le document présente également les liaisons mécaniques, le torseur statique et cinématique des liaisons, ainsi que les différentes hypothèses et définitions nécessaires à l'analyse.