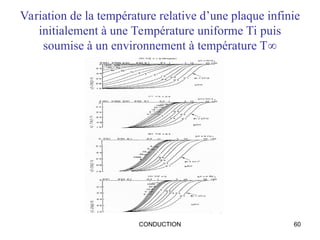
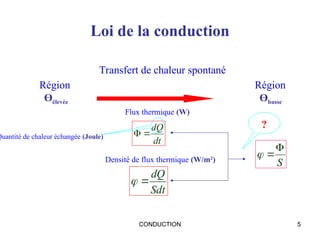
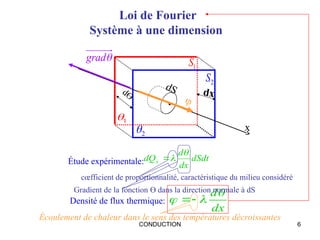
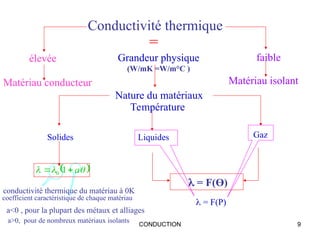
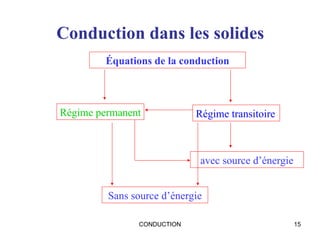
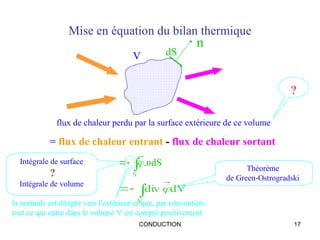
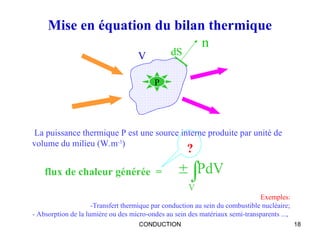
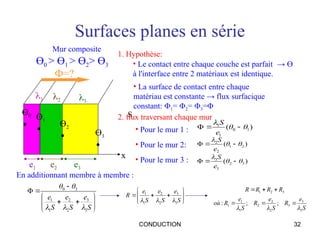
Ce document traite de la conduction thermique, établissant des équations sur le bilan thermique, les lois de conduction et les différentes surfaces (plan, cylindrique, sphérique). Il explique les principes fondamentaux tels que la loi de Fourier, la conductivité thermique des matériaux et les conditions de régime permanent et transitoire. Des applications pratiques et des exemples de calculs illustrent les concepts abordés.










































![CONDUCTION 57
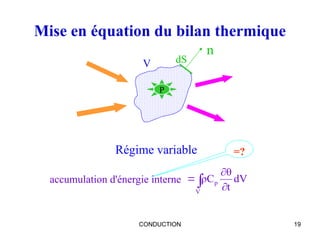
Nombres adimensionnels
• Nombre de Biot:
Définition de la longueur caractéristique:
S
V
Lc
t
CV
hS
T
T
T
T
exp
0
t
L
hL
t
L
L
h
t
CV
S
h
t
cV
hS
c
c
c
c
2
2
[W/(m2
K)]
(W/ m.K)
m
m2
/s
s
m2
c
i
hL
B
2
0
c
L
t
F
•Nombre de Fourier:](https://image.slidesharecdn.com/chapitre2-conduction-241016133750-959422b5/85/Chapitre-2_transfert_thermique-_Conduction-57-320.jpg)